成人男性の身長の平均を知りたい、果汁20%と表示されている缶ジュースが、本当に20%以上含んでいるか検査したい、工場で部品の製造工程を変更したが、それにより部品の長さのばらつきが小さくなったか確認したいなどのとき、すべての人や製品、部品について調べることは困難ですし、コストもかかります。
それで、限られたサンプルを取り出して、全体の状況を推測することになります。このとき、成人男性全体や缶ジュース全体のことを母集団、取り出したサンプルのことを標本といいます。
限られた標本から母集団を推測する統計学の分野を推測統計学といいます。推計統計学を活用することにより、できるだけ少ない標本数で、できるだけ精度のよい推測を行うことができます。その代表的な理論に推定と検定があります。
推定
全国の成人男性(母集団)の身長の平均を知りたいとしましょう。すべての人を調べることは困難ですし、費用もかかります。それで、無作為に成人男性を選び(標本)、その身長を調べることにより、全成人男性の平均身長を推定することになります。
標本として、その身長を測定したところ、次の値が得られました。
170 175 165 180 175 155 165 170 160 185(cm)
問題は、この標本数n=10、標本平均X=170[cm]、標本標準偏差s=9[cm]から、母平均μをどのように推定すればよいかになります。
すべての標本の身長が170cmであれば、μ=X=170[cm]と結論する以外に適切な手段はありません。しかし、実際にはばらつきがありますから、μ=X=170[cm]とと断定することはできません。標本が異なれば、標本平均が異なるからです。
それで、μを1点で推定するのではなく、たとえば、155~185の間というように、区間で推定することになります。しかし、その区間を標本の最小値155と最大値185の間だとするのは、それ以外の標本のデータを用いていないので、不適切だといえます。
また、区間を100cm~300cmのように広くすれば、その間にμがあることは間違いないでしょうし、168cm~175cmのように狭くすれば、その間にあると主張するのは、かなり怪しいでしょう。
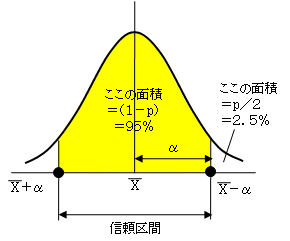
それで、「μが163.5~176.5の間にあることを確率95%でいえる」というようなことを、統計学の理論を用いて示す必要があります。そのための理論を区間推定といいます。そして、この区間のことを95%信頼区間といいます。
ここでは、区間推定の理論や計算方法は省略しますが、おおざっぱにいえば、次のようになります。
標本が無作為に選ばれたとすれば、その標本数が大きければ、図のような分布になるはずです。そして、95%とは、図の黄色部分の面積が95%であり、分布が左右対称であれば、上側および下側の空白の面積が2.5%になることです。その上側の点をX+αとすれば、信頼区間は、
X-α ~ X+α
となります。
また、常識的に次のことがいえます。
・標本の標準偏差sが小さければ、区間は狭くなる。
・標本数nを大きくすれば、区間は狭くなる。
・有意水準を厳しくすれば、区間は広くなる。
ここで、「母平均μの95%信頼区間は163.5~176.5である」とは、「μが163.5~176.5にある確率が95%である」と解釈するのは、厳密には不適切なのです。私たちが知らないだけで、μは唯一の値として存在するのです。既に決定しているものを、確率的に捉えるのは不合理です。
「標本を取り出して推定することを多数回行えば、μの値を正しく推定できるのだが、都合により1回しか行えない。それで163.5~176.5という幅を設けたのだ。95%とは、もし100回同じような推定を行ったとすれば、そのうち95回は、平均が163.5~176.5の間に入ると推定される」というのが適切な解釈なのです。
検定
果汁20%と表示されている缶ジュースについて、10個の標本を得て、果汁含有量を調べたところ、平均18%、標準偏差3%の値を得ました。平均では20%に達していませんが、標本数が少ないため、たまたま低くなったのかもしれません。これで、20%より少ないと決めつけられるでしょうか。検定とは、このような問題を解くための理論です。
検定では、
帰無仮説 H0:μ=20%
対立仮説 H1:μ<20%
という2つの仮定を設定します。
H0とは、標本の果汁含有量平均s=18は、母集団μ=20よりも小さいのですが、たまたまこの標本がそうなっただけで、本当はμ=20、σ=3の母集団に属しているのだという仮説です。このような調査を数多く行うことができれば、sは20に近くなるのだという仮説です。
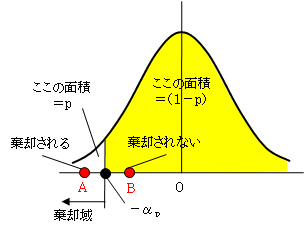
そして、H0であると仮定し、それが実現する確率を計算して、その確率が非常に小さく(5%や1%など未満であれば)、図のAのような棄却域に入るので、H0が棄却されたと結論するのです。
棄却されたとは、設定した有意水準において対立仮説H1が成立することです。「μ=20だとすると、あまりにも通常ではないことが起こったことになる。それよりもμ<20であると考えるほうが妥当だろう」という意味です。そして、有意水準5%とは、「この結論が誤りである確率は5%以内である」ということです。
もし、この計算値が図のBのように、黄色の範囲になったときは、H0は棄却されません。棄却されない(有意差がない)とは、「あることが起こったが、この程度は通常ありうることなので、μ=20であることもあり得る。μ<20だとはいいきれない」ことになります。決して「μ=20%であることが、確率95%で証明された」という意味ではありません。
平均と標準偏差
ここまで、説明なしに、平均と標準偏差を用いてきました。この2つが、分布のようすを特定する尺度なのです。
母集団の身長、果汁含有量、部品の長さなどの測定量をヒストグラムにすると、母集団が大きければ、平均を中心にして、左右対称な釣鐘型の分布(正規分布)をしていると考えられます。
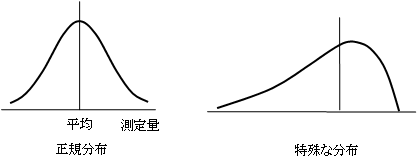
実際には「特殊な分布」になっていることもありますが、適当な変換をすることにより正規分布に近似させることができます。また、そのような分布を対象にした理論もあります。しかし、ここでは正規分布であるとしておきます。
この分布を特徴づける統計量に、平均と標準偏差(統計学では標準偏差よりも、その2乗である分散を用いることが多い)があります。平均は、測定量の大きさの尺度になるものですし、標準偏差(分散)は、ばらつきの尺度になるものです(通常、母集団の平均をμ、母集団の標準偏差をσで表記します)。
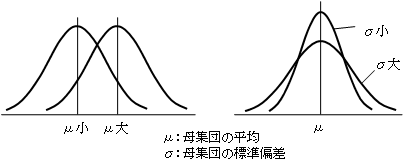
逆にいえば、2つの分布で、平均μと標準偏差σが一致すれば、それらの分布は同じである(同じ母集団に属する)とするのです。
統計分布
また、ここまで単に「分布」といってきました。ここで、代表的な統計分布を紹介します。
母集団は個数が非常に大きいので正規分布になりますが、標本数が少ないときは正規分布になりません(その理由は省略)。そして、統計学の理論により、少ない標本での平均Xや標準偏差sに関して、どのような分布になるかが定式化されています。
そのような分布を総称して統計分布といいます。統計分布の代表的なものに、正規分布、t分布、χ2分布(カイ2乗と読む)、F分布などがあります。
- 正規化
- 測定量Xは170cmとか50グラムというように、数値も物理単位もまちまちですし、標本数nも異なります。それでは取扱いが不便なため、たとえば、Z=(X-X)/n のような変換をして、平均=0、分散=1にします。このような変換を正規化といいます。
正規化した統計分布に関して、数表が作成されています。 (→正規分布表、t分布表、χ2分布表、F分布表) - 自由度φ
- 推計統計学では、自由度という概念がよく用いられます。自由度の説明は難解です。単純にいえば、各種の統計計算では、n個の平均を求めて多くの計算に用いますが、平均がわかれば、n個のデータのうち1個はわかります。それで、自由に変えることができるデータはn-1個になります。それを自由度というのです。ここでは、n-1のことだと知っていれば十分です。
- 有意水準
- 標本から母集団の平均や分散などを推測するのに、「○%の確率でいえる」というような表現になります。この○%のことを有意水準といいます(厳密ではない)。そして、慣習的に5%(95%)、1%(99%)がよく用いられます。すなわち、「20回に1回、100回に1回程度は結論と異なることがあるかもしれないが、このようなことがいえる」とするのです。社会科学の分野では、10%を用いることもあります。上記の数表の多くは、これらの%について作成されています。
代表的な検定
それぞれの統計分布に対応した検定方法があります。それをパラメトリック検定といいます。
- Z検定
- 正規分布を用いる統計学的検定法で、標本の平均と母集団の平均の差の検定
- F検定
- 二つの母集団AとBの分散比が等しいかどうかの検定。分散分析
- t検定
- 母集団の平均の推定、グループの間で平均に差があるかを検定。相関・回帰係数
・分散が等しいとき:スチューデント(Sstudent)のt検定、単にt検定というときこれを指す。
・分散が等しくないとき:ウェルチ(Welch)のt検定 - カイ二乗検定
- クロス集計表など、発生する頻度(度数)について偏りがあるかどうかを検定
つのグループの独立性の検定
データが少ない場合はフィッシャーの正確確率検定 - ノンパラメトリック検定
- 特定の分布を仮定しない統計的検定。順序変数や質的変数に適用