ｔ分布と推定・検定

ｔ分布とは、平均に関する統計分布です。標本の平均と標準偏差から、母集団の平均を推定したり、２つのグループの間で平均に差があるかを検定したりするときに用いられます。
　代表的なｔ検定には、２つのグループの分散が等しいかどうか（Ｆ検定）により次の２つがあります。
　・分散が等しいとき：スチューデント（Sstudent）のｔ検定、単にｔ検定というときこれを指す。
　・分散が等しくないとき：ウェルチ（Welch）のｔ検定

平均μ、標準偏差σの正規分布になっている母集団から取り出したｎ個の標本の平均をμ₀、標準偏差をｓとすると、
　　　　　　μ₀－μ
　　　ｔ＝─────
　　　　　ｓ／√ｎ
は、自由度ｎ－１のｔ分布に従う。

（Excel関数：TDIST(数値,自由度、片側・両側指定)、逆関数 TINV(確率,自由度)
ｔ分布の数表、計算プログラム）

平均の区間推定

● 例題ｔ・１
成人男性１０人を無作為に選び身長を測定したところ、次の結果を得た。
　　170, 175, 165, 180, 175, 155, 165, 170, 160, 185 [cm]
成人男性全体の平均μの９５％信頼区間を求めよ。
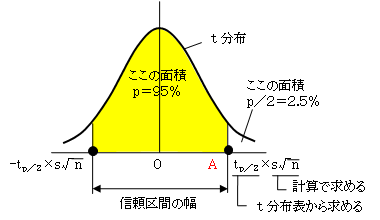● 解答
９５％信頼とは、図の黄色の部分が９５％ということですから、片側の無色の部分は２.５％になります。
ｔ分布表から、自由度ｎ－１＝９、２.５％のｔの値を求めるとｔ＝２.２６２になります。
また、標本の個数ｎ＝１０、標準偏差ｓ＝９ｃｍから、
　　　ｓ／√ｎ＝９／１０＝２.８４６
になります。
従って、この信頼区間は、
　　　μ₀±（ｔ×ｓ／√ｎ）
　　　＝１７０±（２.２６２×２.８４６)＝１７０±６.４
　　　＝１６３.６～１７６.４［ｃｍ］
となります。
● 補足
［有意水準と信頼区間の関係］
９９％信頼区間は、黄色の部分が大になるので、Ａ点はもっと右になり、信頼区間は広くなります。
自由度９、０.５％のｔは３.２５０ですので、ｔ×ｓ／√ｎ＝９.３になります。
信頼区間は、１６０.８～１７９.３
［標本数と信頼区間の関係］
標本数が母集団の数と一致すれば、μ＝μ₀になります。それからもわかるように、標本数が大ならば、信頼区間は狭くなります。たとえば標本数が１００ならば、その標準偏差ｓが上と同じ９ｃｍであっても、
　　　ｓ／√ｎ＝０.９、　ｔ（２.５％、自由度９９）＝１.６１
　　∴ｔ×ｓ／√ｎ＝１.６１×０.９＝１.４４
信頼区間は、１６８.５６～１７１.４４になります。

平均の検定

● 例題ｔ・２
ある全国規模の試験では、平均点がμ＝５０点であったことが公表されている。ある学校で無作為に選んだ１６人について調査したとろ、平均点はμ₀＝５５点、標準偏差はｓ＝１０点であった。この学校の成績は、全国と比較して高いといるかどうか。有意水準５％で検定せよ。
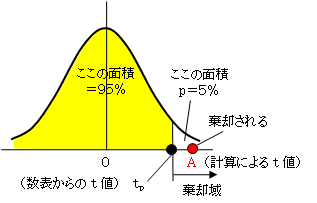● 解答
　　帰無仮説　Ｈ₀：μ₀＝５０
　　対立仮説　Ｈ₁：μ₀＞５０
大きいかどうかなのだから、片側確率５％で考えます（全国と比べて差があるかならば２.５％を用いる）。
ｔ分布表から、自由度１５、有意水準ｐ＝０.５％のｔの値はｔ_p＝１.７５３です。
標本からの計算によるｔの値は、
　　　　　　μ₀－μ　　　　５５－５０
　　　ｔ＝─────　＝　───────　＝　２
　　　　　ｓ／√ｎ　　　　１０／√１６
計算値は図のＡの位置になり、棄却域に入るので、Ｈ₀：μ₀＝５０よりもＨ₁：μ₀＞５０のほうが確からしいといえます。すなわち、この学校の成績は全国平均よりも高いことが有意水準５％でいえることになります。

平均の差の検定

● 例題ｔ・３
ＡとＢの農場で収穫した作物の重さを測定した結果は次の通りであった。
　　Ａ　38.6　40.4　30.8　42.2　34.2　36.8　38.4　31.8　39.4　37.4
　　Ｂ　29.0　30.6　32.8　32.2　37.2　32.8
ＡはＢよりも重いといえるかどうか。有意水準５％で検定せよ。
● 解答
例題ｔ・１とｔ・２では、比較の一方が非常に個数の大きな母集団でした。本問では双方が標本です。このような場合でもｔ検定が用いられます。
Ａ、Ｂそれぞれの標本数ｎ、自由度φ、平均μ、標準偏差ｓに添字ａとｂをつけると、２つを合わせた標準偏差ｓおよびｔは次の式で求められます（理由は省略）。

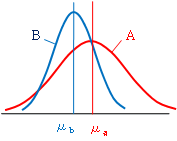
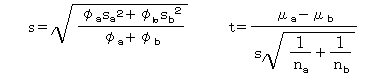
そして、
　　帰無仮説　Ｈ₀：μ_a＝μ_b
　　対立仮説　Ｈ₁：μ_a＞μ_b
となります。
片側５％、自由度１４（＝φ_a＋φ_a）のｔ値は１.７６になります。
一方、上の式に、
　Ａ　ｎ_a＝10,　φ_a＝9,　μ_a＝37.0,　ｓ_a＝3.69
　Ｂ　ｎ_b＝ 6,　φ_a＝5,　μ_b＝32.4,　ｓ_b＝2.76
を代入すると、ｓ＝３.３９、ｔ＝２.６３となります。
計算による値のほうが大きいので、有意差があるといえます。

（注意）３群以上ではｔ検定は使えない

Ａ、Ｂ、Ｃの群について、Ａ－Ｂ間、Ｂ－Ｃ間、Ｃ－Ａ間の３回のｔ検定を行ったとき、
　　すべての組み合わせで差が出ない確率
　　＝ (A-B間で差が出ない確率) * (B-C間で差が出ない確率) * (C-A間で差が出ない確率)
となります。
　有意差水準を０.０５とすると、この３つの確率は０.９５となり、全体では０.８５７になります。
　　　少なくともひとつの組み合わせに差が出る確率
　　　＝１－すべての組み合わせで差が出ない確率
なので、０.１４３となります。

この０.１４３は有意差水準０.０５よりかなり大きな値です。
　このように、ｔ検定を繰り返すと、本当は有意差がないのに差があるとしてしまう確率が高くなってしまうのです。これを検定の多重性による第一種の過誤といいます。
　そのため、３群以上の平均の差の検定にはｔ検定は使えません。分散分析など他の方法を用います。