χ２（カイ２乗）分布は、分散に関する統計分布です。標本の平均と分散から、母集団の分散を推定したり、２つのグループの間で分散に差があるかを検定したりするときに用いられます。分散を重視するのは、品質管理の分野では、ばらつきを少なくすることが重要だからです。
分散σ2の正規分布になっている母集団から取り出したｎ個の標本の分散をｓ2とすると、
（ｎ－１）ｓ2
χ2＝──────
σ2
は、自由度ｎ－１のχ2分布に従う。
（Excel関数：片側確率 CHIDIST(確率,自由度)、逆関数 CHIINV(確率,自由度)
χ2分布の数表、計算プログラム）
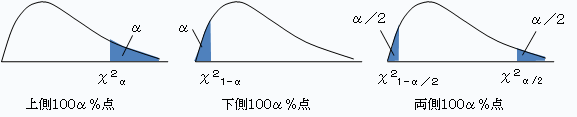
χ2分布表を見るときには、
上側５％のときは、α＝０.０５の欄
下側５％のときは、α＝０.９５の欄
両側５％のときは、α＝００２５の欄とα＝０.９７５の欄
を用います。
- 分散の区間推定
-
● 例題ｃ・１
ある薬品について、１０個の標本の成分を分析したところ、次の結果を得た。
24, 22, 28, 26, 30, 28, 20, 22, 24, 26 [cm]
母分散の９５％信頼区間を求めよ。
● 解答
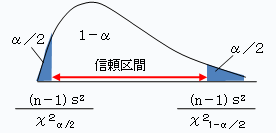
母分散σ2の１００（１－α）％信頼区間は、
下限 上限
（ｎ－１）ｓ2 （ｎ－１）ｓ2
────── ──────
χ2α／２ χ2１－α／２
で求められます。
標本より、標本数ｎ＝１０、分散ｓ2＝１０になります。
９５％からα／２＝０.０２５、１－α／２＝０.９７５になります。
χ2分布表から、自由度９（１０－１）の０.０２５と０.９７５の値は、それぞれ、１９.０２、２.７０になります。
これを、上の式に代入すると、
９×１０ ９×１０
下限＝─────＝４.７３ 上限＝─────＝３３.３
１９.０２ ２.７０
になります。
すなわち、求める信頼区間は、４.７３～３３.３になります。 - 分散の検定
- ● 例題ｃ・２
ある袋詰めの製品がある。従来の工程では分散が４であった。ばらつきを小さくするために工程を改良した。新工程で１０個の標本を測定したところ、分散は３になっていた。このことから、新工程で改良の効果があったか、有意水準９５％で検定せよ。
● 解答
分散の検定は、数表から求めたχ2の値と、
（ｎ－１）ｓ2
χ20＝──────
σ2
で求めたχ20の値を比較することにより行います。
［上側検定のとき］
Ｈ0：ｓ2＝σ2、 Ｈ1：ｓ2＞σ2の場合、 χ20＞χ2α ならＨ0を棄却します。
［下側検定のとき］
Ｈ0：ｓ2＝σ2、 Ｈ1：ｓ2＜σ2の場合、 χ20＜χ2１－α ならＨ0を棄却します。
［両側検定のとき］
Ｈ0：ｓ2＝σ2、 Ｈ1：ｓ2≠σ2の場合、 χ20＜χ21-α/2 あるいは χ20＞χ2α/2 ならＨ0を棄却します。
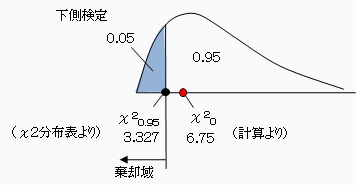
例題は下側検定です。自由度９ですから、χ2０.９５＝３.３２５です。
そして、
（ｎ－１）ｓ2 (１０－１）×３
χ20＝──────＝────────＝６.７５
σ2 ４
ですから、χ20（６.７５）＞χ2０.９５（３.３２５）になり、Ｈ0は棄却されません。すなわち、改良による効果があったとはいえません。