正規分布とは
例えば、すべての成人男子の身長Xを測定してグラフにすると、下左図のようなグラフになります。
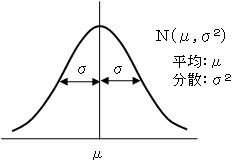
このとき、Xは、平均μと分散σ2(標準偏差σ)の正規分布に従うといいます。
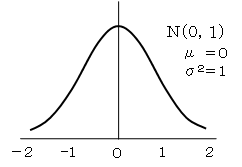
そして、Z=(X-μ)/σ とおくと、Zは平均0、分散1の標準正規分布(下右図)に従います。
正規分布表
標準正規分布では、Zが決まれば、P(≧Z)の表が計算されています。それを 正規分布表 といいます。主な値を掲げます。
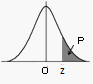 |
Z P |
数値例
成人男子の平均身長は170センチ、標準偏差は10センチであることがわかっているとします。
180センチ以上の人は何%でしょうか?
μ=170、σ=10、X=180なので、
Z=(X-μ)/σ=(180-170)/10=1
このときのPは0.135→13.5%・・・答
成人男子の90%の身長は、どの範囲になるでしょうか?
それ以外の10%の人は高い場合と低い場合があります。高い場合は5%なので、P=0.05
P=0.05対するZは1.65
求める範囲は、μ±Zσ=170±1.65×10=153.5~186.5[センチ]・・・答
中心極限定理
ある母集団の分布はわからないが、平均μと分散σ2はわかっているとします。
その母集団から、n個の標本xiを取り出したとき、標本平均xの確率分布は、nが十分に大きい(n≧12程度)ならば、その母集団の分布がどのようなものであっても、平均μ、分散σ2の正規分布に近づくことが証明されています。これを中心極限定理といいます。
「インターネット利用者全体で、各人が毎日何通の電子メールを受け取っているかの分布は不明だが、平均50通で標準偏差は8通であることがわかっている。あるグループの16人を選んで調べたとき、その平均が54通以上である確率を求めよ。」という問題を考えます。
標本平均の分布は、
平均:50通
標準偏差:√σ2/n
=√82/16=2通
の正規分布に従います。すなわち、Z=(x-50)/2とすれば、Zは標準正規分布に従います。
そして、(54-50)/2=2ですから、正規分布表からP=0.023。すなわち、平均が54通以上である確率は2.3%となります。
これにより、このグループはインターネット利用者全体からみると、かなり電子メールを多く受け取っている人たちだと結論することができます。