データの特徴を表すには、データの大きさとバラツキの程度を示すのが一般的です。そのための概念を列挙します。
例えば、10、20、30、40、50の5個(n=5)のデータがあるものとします。単位はm(メートル)です。
| 記号と計算式 | 計算値と[単位] | 意味 | |
| データ数 | n | 5[個] | |
| 最小値 | 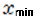 | 10[m] | |
| 最大値 | 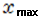 | 50[m] | |
| 合計 | 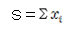 | 150[m] | = 10 + 20 + 30 + 40 + 50 |
| 平均 | 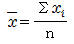 | 30[m] | データの大きさを示す尺度です。 |
| 中央値 (メディアン) | 昇順にならべた ときの中央の値 | 30[m] | 偶数個ののときは中央2個の平均 (四分位数:小さい順に4等分したときの値) |
| 最頻値 (モード) | 最もデータ数の多 い値「意味」参照 | 20[m] | データが次のとき 10,20,20,20,30,30,40,50 |
| 偏差平方和 | 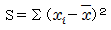 | 1000[m2] | (xi-x)を偏差といいます。偏差の大きさを示すのに、偏差を単純に合計したのでは0になるし、絶対値での処理は面倒なので、偏差2の合計で示すのです(*注1) |
| 分散 | 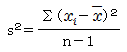 | 250[m2] | バラツキの尺度です。データ数が大ならば偏差平方和も大きくなるので、その平均をとることにより、データ数の影響をなくします。ところが、推計統計論では、個数(n)ではなく、自由度(n-1)を用います(その理由はここでの範囲を超えるので省略)。 |
| 標準偏差 | 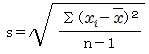 | √250 =15.8[m] |
分散では単位がm2になっているので、√分散とすることで、元のデータと同じ単位にします。 |
| 変動係数 | 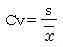 | 0.527[-] | 標準偏差÷平均値とすることにより、データの単位や大きさの影響をなくすことができます。これで、一般的なバラツキの尺度とすることができます。 |
| 平均偏差 | 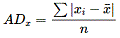 | 60/5 =12[m] | 平均との差の絶対値÷個数。 |
(*1)偏差平方和の計算
x xi-x (xi-x)2
10 -20 400
20 -10 100
30 0 0
40 10 100
50 20 400
1000 ←偏差平方和
なお、Σ(xi-x)2 は、次のように変形することができます。
Σ(xi-x)2
(↓ (a-b)2=a2-2ab+b2)
=Σxi2-2xΣxi+x2Σ1 (↓ Σxi=nx)
=Σxi2-2nx2+nx2
=Σxi2-nx2
=102+202+・・・+502-5×302
=100+400+・・・+2500-4500=1000 (上表と一致)
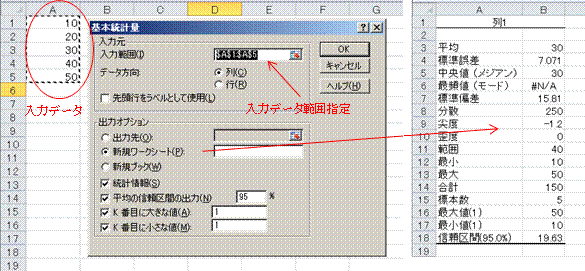
Excelによる基本統計量の計算
Excelで、[データ]→[データ分析]→[基本統計量]を用います。
y=Ax+Bとしたとき
元のデータxをy=2x+6にしたとき、すなわち、26、46、66、86、106としたとき、上の諸元がどのように変わるかを考えます。
- 平均
- 合計は、26+46+66+86+106=2(10+20+30+40+50)+6×5になります。一般的には、Anx+Bnになります。それで平均はAnx+Bnになり、この場合は2×30+5=65になります。
- 偏差平方和、分散
- 偏差は、26-65=-40、36-65=-20、・・・、105-65=40のように2倍になり、偏差平方和は、1600+400+・・・+1600=40000になります。すなわち偏差平方和は元のA2倍になりBには無関係です。分散もA2倍になりBには無関係です。
- 標準偏差
- 標準偏差は√分散なので、A倍になります。
- 変動係数
- 標準偏差がAsになり、平均がAx+Bになるのですから、B=0のときの変動係数は元のCVと同じ値になります。
データの個数がM倍になったとき
例えばMが2で、10、20、30、40、50、10、20、30、40、50の10個のデータの場合はどうなるかを考えます。
- 平均、偏差平方和
- 平均は変化せず、偏差平方和がM倍になることは明らかです。
- 分散、標準偏差、変動係数
- データの個数はMn個ですから、その自由度はMn-1になります。それで、この分散はMs2/(Mn-1)になります。すなわち、M(n-1)/(Mn-1) 倍になります。
ここで、nが十分に大きいと、この式は1に近づきます。すなわち、nが十分に大きいときは、分散は元と変わらないことになります。
標準偏差と変動係数もnが十分に大きいときは、元と同じになります。
L組のデータを加えたとき
例えば、1日目の出荷が5回あり、それぞれ10,20,30,40,50個でした。2日目の出荷も同じでした。そのとき2日間の平均や標準偏差はどうなるかというように、L組の合計を考えます。
- 平均
- 各日の平均をxとすれば、L日間ではLxになります。
- 偏差平方和
- ここで、偏差はすべてのデータLn個の平均からの偏差ではなく、それそれの組のなかでの平均からの偏差です。それで、それで、全体の偏差平方和は各組の偏差平方和の合計となります。すなわち、L倍になります。分散の計算での自由度もn-1です。それで分散もL倍になります。
- 標準偏差
- 分散がL倍になるのですから、標準偏差は√L倍になります。これは重要な事項です。
- 変動係数
- 標準偏差が√L倍、平均がL倍になるので、変動係数は1/√L倍になります。
以上をまとめると、次表になります
| Ax+B | データ個数M倍 | L組の合計 | |
|---|---|---|---|
| 平均 | Ax+B | 元と同じ | L倍 |
| 偏差平方和 | A2倍 | M倍 | L倍 |
| 分散 | A2倍 | 元と同じ(注2) | L倍 |
| 標準偏差 | A倍 | 元と同じ(注2) | √L倍 |
| 変動係数 | 元と同じ (注3) | 元と同じ(注2) | 1/√L倍 |
注2:nが十分に大きいとき
注3:B=0のとき
標本の平均と分散
母集団の平均や分散を知りたいとき、母集団すべてを調べることは不可能なので、いくつかの標本(サンプル)を取り出して、その平均や分散を測定して、それらから母集団の平均や分散を推定することになります。それで、母集団と標本での平均と分散の関係を知ることが必要になります。
そのような理論を推測統計といいますが、ここでは、その最も基本的な「点推定」について、結果だけを示します。
平均μ、分散σ2の母集団からn個の標本を取り出したとき、標本の平均μ0と平均の分散σ20は次の式で与えられます。
μ0=μ、 σ20=σ2/n
中央値(メディアン)と平均偏差
これらは、平均と標準偏差に対応するものですが、統計学的な意味づけよりも実務の観点を重視したものです。特に極端な異常値が存在する場合、その影響を少なくすることができます。
データが、10、20、30、40、200のように極端な値がある場合、平均は60になりますがこの5つのデータの代表値とするよりも中央の30を代表値とするほうが適切なことがあります。同様に分散も極端な値があるとそれが2乗されるので、標準偏差も非常に大きくなってしまいます。
むしろ、偏差を用いないで四分位数(昇順にならべたときの小さいほうから。1/4、2/4、3/4の点)を求めるほうが実際の分布をよく示すようなこともあります。