正規分布とは、平均を中心に左右対称の釣鐘型をした分布です。成人男子の身長、リンゴの重さ、製品の形状など、多くの物理量の分布は正規分布になることが知られています。
正規分布による検定をｚ検定と呼ぶこともあります。
Ｘが、平均μ、標準偏差σの正規分布に従う母集団に属するとき、
Ｚ＝（Ｘ－μ）／σ
の変換を行ったＺは、平均０、標準偏差１の標準正規分布に従う。
（Excel関数：NORMDIST(値,平均,標準偏差,密度・累積)、逆関数 NORMDIST(確率,平均,標準偏差)
正規分布の説明、数表、計算プログラム）
- 区間推定
-
● 例題ｎ・１
ある大規模の試験の成績が、受験者全体の平均点μは５０点で、その標準偏差σは１０点であることが公表されている。このことから、受験者の９５％は何点から何点の間にあると推定できるか（有意水準５％での信頼区間を求めよ）。
● 解答
平均μと標準偏差σのとき、点数Ｘを、
Ｚ＝(Ｘ－μ)／σ
により正規化すると、Ｚは平均０、分散１の標準正規分布に従います。
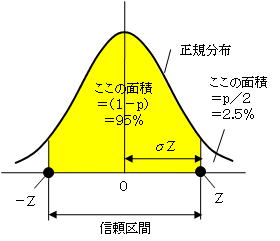
図の黄色の部分の面積を９５％にするＺの値を求めたいのですから、一方の確率は２.５％になります。
正規分布表より、０.０２５となるＺを求めると、１.９６になります。
また、上の式を変形すると、Ｘ＝μ＋σＺ になります。それで、推定される範囲は、
μ－σＺ≦Ｘ≦μ＋σＺ
となります。
これに、μ＝５０、σ＝１０、Ｚ＝１.９６を代入すれば、求める区間は、
３０.４～６９.６
となります。
- 点の検定
-
● 例題ｎ・２
ある菓子の通常の重さは、平均μ＝１５０グラム、標準偏差σ＝２グラムである。たまたまＸ＝１４５グラムの製品が見つかった。工程に菓子を小さくするような何らかの原因が発生したと考えるべきか。有意水準５％で検定せよ。
● 解答
この場合は、
帰無仮説 Ｈ0：Ｘは平均μ、標準偏差σの母集団に属する
対立仮説 Ｈ1：Ｘは母集団よりも軽い
になります。
Ｈ0だとすれば、Ｚ＝(Ｘ－μ)／σにより正規化すると、Ｚは平均０、分散１の標準正規分布に従がいます。
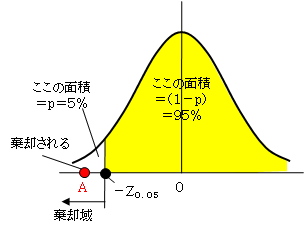
Ｐ（≧Ｚ）の値は正規分布表になっています。Ｐ（≧Ｚ）＝０.０５になるＺは
Ｚ0.05＝１.６４
です。
正規分布は左右対称であり、この場合は、小さいほうを検討しているので、棄却域の点は
－Ｚ0.05＝－１.６４
になります。
一方、１４５グラムからのＺは、
Ｚ＝(Ｘ－μ)／σ＝（１４５－１５０）／２＝－２.５
となります（Ａ点）。 Ａ点は棄却域に入っているので、Ｈ0は棄却されます。Ｈ0は棄却されたということは、Ｈ1が採用されるということです。すなわち、有意水準５％（信頼度９５％）で、菓子を小さくするような何らかの原因が発生したといえることになります。
- 比率の検定
-
● 例題ｎ・３
ある硬貨を１００回投げたとき、表が５６回出た。この硬貨は表が出やすいような原因があるのだろうか。
● 解答
この場合は、 帰無仮説 Ｈ0：μ＝０.５（通常の硬貨である）
対立仮説 Ｈ1：μ＞０.５（表が出やすい）
になります。
試行回数ｎが少ないときは、２項分布によって計算できますが、試行回数が大きいときは困難です。
「２項分布は、ｎ×ｐが大きいときは、平均ｎｐ、標準偏差√ｎｐ（１－ｐ）の正規分布で近似できる。」という性質があります。
これを用いると、
μ＝ｎｐ＝＝１００×０.５＝５０
σ＝√ｎｐ（１－ｐ）＝√１００×０.５×０.５＝５ の正規分布で近似できるので、
Ｚ＝（５６－５０）／５＝１.２
（厳密には、５６ではなく、５６－０.５とすべきだが、その理由は省略）
となります。 一方、正規分布表より上側５％点は１.６４５なので、「通常の硬貨である」との帰無仮説は棄却されません。すなわち、有意水準５％では、この硬貨に表が出やすい原因があるとはいえないのです。