Ｆ分布と推定・検定

Ｆ分布は、二つの母集団ＡとＢの分散比（σ_a²／σ_b²）に関する統計分布です。分散はばらつきの尺度ですから、その差ではなく比で比較するのが適切です。

二つの母集団ＡとＢからの標本の個数をｎ_a、ｎ_b、分散をｓ_a2、ｓ_b2とすると、分散比
　　　F＝ｓ_a2／ｓ_b2
は、自由度（ｎ_a－１、ｎ_b－１）のＦ分布に従う。

（Excel関数：FDIST(値,自由度１,自由度２)、逆関数 FINV(確率,自由度１,自由度２)
Ｆ分布の数表、計算プログラム）

分散比の検定

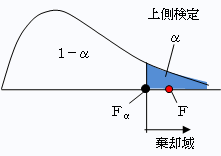
● 例題ｆ・１（上側検定）
ある部品を生産するのに、２つの工程Ａ、Ｂが考えられる。それぞれの工程による部品の標本を測定したところ、次の値を得た。これより、工程Ａは工程Ｂよりも分散が大きいといえるか。有意水準５％で検定せよ。
　　　工程Ａ　ｎ_a＝１０　　ｓ_a2＝６.１
　　　工程Ｂ　ｎ_b＝１６　　ｓ_b2＝２.２
● 解答
標本からの分散比は、
　　　Ｆ＝ｓ_a2／ｓ_b2＝６.１／２.２＝２.７７３＞１
この場合は、上側での検定なので、Ｆ_0.05との比較になります。
Ｆ_0.05分布表の、自由度（横）ｎ_a－１＝９、自由度（縦）ｎ_b－１＝１５の値は、２.５８８です。
　　　Ｆ＞Ｆ_0.05
になるので、工程Ａは工程Ｂよりも分散が大きいといえます。
　なお、有意水準１％では、Ｆ_0.01＝３.８９５になり、Ｆ＜Ｆ_0.01になるので、工程Ａは工程Ｂよりも分散が大きいとはいえないことになります。
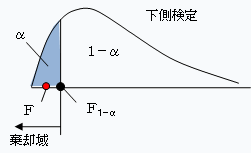
● 例題ｆ・２（下側検定）
ある部品を生産するのに、２つの工程Ａ、Ｂが考えられる。それぞれの工程による部品の標本を測定したところ、次の値を得た。これより、工程Ａは工程Ｂよりも分散が小さいといえるか。有意水準５％で検定せよ。
　　　工程Ａ　ｎ_a＝１６　　ｓ_a2＝２.２
　　　工程Ｂ　ｎ_b＝１０　　ｓ_b2＝６.１
（例題ｆ・１と逆の関係になっています）
● 解答
標本からの分散比は、
　　　Ｆ＝ｓ_a2／ｓ_b2＝２.２／６.１＝０.３６１＜１
となり、下側での検定なので、Ｆ_0.95との比較になります。
ここで、次の公式があります。

自由度（ｎ_a－１、ｎ_b－１）の下側１００α点をＦ_１－α
自由度（ｎ_b－１、ｎ_a－１）の上側１００α点をＦ_α
とすると、
　　　Ｆ_１－α＝１／Ｆ_α
の関係が成立する。

この場合、自由度（９、１５）のＦ_0.05は２.５８８ですから、自由度（１５、９）のＦ_0.95は、
　　　Ｆ_0.95＝１／Ｆ_0.05＝１／２.５８８＝０.３８６
になります。
　　　Ｆ＜Ｆ_0.95
になるので、工程Ａは工程Ｂよりも分散が小さいといえます。
　なお、有意水準１％では、
　　　Ｆ_0.99＝１／Ｆ_0.01＝１／３.８９５＝０.２５７
になり、Ｆ＞Ｆ_0.01になるので、工程Ａは工程Ｂよりも分散が小さいとはいえないことになります。