スタートページ >
JavaScript >
ライブラリ目次
数値解析関連 JavaScript関数ライブラリ na.js の利用解説書
ご利用にあたって
代数系 f(x) を指定する
代数方程式 f(x) = 0 の根:はさみうち法コード表示 コード表示
はさみうち法による f(x) = 0 の解(参照:「方程式の根」 )を求める。
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
naFx0HasamiuchiPl 代数方程式 f(x) = 0 の複数の実根:はさみうち法コード表示 コード表示
はさみうち法による f(x) = 0 の1個の実数解を求める関数にはnaFx0Hasamiuchi があります。
コードをダウンロードするときには、naFx0Hasamiuchi もダウンロードしてください。
ケース1
入力Trace
Return
ケース2
Trace
Return
方程式の根(ニュートン法)コード表示 コード表示
ニュートン法により、方程式の実根を求める。n = xn-1 - f(xn-1 )/f'(xn-1 ) (f'=df/dx)「方程式の根」
fxは文字列として、" "で囲む。eps を省略すると 0.001 になる、
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
naFx0NewtonPl 代数方程式 f(x) = 0 の複数の実根:ニュートン法コード表示 コード表示
ニュートン法による f(x) = 0 の1個の実数解を求める関数にはnaFx0Newton があります。
コードをダウンロードするときには、naFx0Newton もダウンロードしてください。
ケース1
入力Trace
Return
ケース2
Trace
Return
3次方程式の複素数根 a0 + a1 x + a2 x2 + a3 x3 = 0 コード表示 コード表示
a3 を省略すると2次方程式、さらにa2 を省略すると1次方程式になる。
ケース1
入力3 - x + 1 = 0Trace実行
Return実行
ケース2
Trace実行
Return実行
数式 f(x) を最大にする xコード表示 コード表示
数式 f(x) が最大となるxの値を戻します。
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
代数式 f(x) のxにおける微分係数aコード表示 コード表示
fxのxにおける微係数aを求めます。xの近傍の2点 x-d*xとx-d*xでの勾配をa0とし、dを1/2にしたときの勾配aとの差が、相対誤差 |(a-a0)/a| < eps になるまで繰り返します。
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
微分方程式(ルンゲクッタ法)コード表示 コード表示
一階微分 dy/dx = f(x,y) の式を与えて y(x+dx) = y(x) + a*dx の a の値を、4次のルンゲクッタ法により求めます。
ルンゲクッタ法では、次のステップで定義します。a = (k1 + 2*k2 + 2*k3 + k4) / 6
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
微分方程式(ルンゲクッタ法)作表コード表示
一階微分 dy/dx = f(x,y) の式を与えて 4次のルンゲクッタ法により x = xmin~xmax に対応する y の値、および関連する値を算出します(y0 は x = xmin のときの y の値)。
実行
連立微分方程式(ルンゲクッタ法)コード表示 コード表示
二つの一階微分 dx/dt = f(x,y), dy/dt = g(x,y) の式を与えて、x(t+dt) = x(t) + ax*dt, y(t+dt) = y(t) + ay*dt となる偏微分係数 ax, ay の値を
ルンゲクッタ法では、次のステップで定義します。a = (k1 + 2*k2 + 2*k3 + k4) / 6
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
連立微分方程式(ルンゲクッタ法)作表コード表示
二つの一階微分 dx/dt = f(x,y), dy/dt = g(x,y) の式と t = tmin における x0, y0 を与えて、t = tmin~tmax (刻み dt)での x(t), y(t) などを表の形式で戻します。
t: t[i] = t t = tmin, tmin+dt, tmin+2*dt, …, tmax の値実行
数式 f(x) の極値(複数)コード表示 コード表示
数式 f(x) の極値 f'(x) が正から負へ、負から正に変化する点(複数)を戻します。i i が極大なら1、極小なら-1ケース1
入力
var fx= "x*(x-1)*(x-2)";Trace実行
Return実行
ケース2
Trace実行
Return実行
代数式 f(x) の定積分(シンプソン則)コード表示 コード表示
シンプソン則は、2次式で近似します。0 (=xmin),x1 ,x2 ,....,x2n (=max)i に対応するfxの値を yi とすると)0 +y2n )+4(y1 +y3 +...y2n-1 )+2(y2 +y4 +...y2n-2 ) }「定積分」
最初のn2で計算した値をs0、次にn2を2倍(すなわちキザミ幅を1/2)にして計算した値を s として、相対誤差 |(s-s0)/s| <eps となるまで繰り返します。
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
漸化式の特性方程式
漸化式の係数と初期値を与えて、an の一般解を「文字列」として戻します。 an+1 =p*xn +qコード表示 コード表示
an+1 =p*xn + q + rnコード表示 コード表示
an+1 =p*an + q*rn コード表示 コード表示
an+1 =p*an q コード表示 コード表示
a1 および(あるいは)p が負数のときは、q を整数に限定しています。
an+2 =p*an+1 + q*an コード表示 コード表示
特性方程式の判別式 D = q2 + 4q の正負により、計算方法が異なります。
多点系 点(x,y) を与える
多点系 最小二乗法
最小二乗法(1次式)y = a[0] + a[1]x コード表示 コード表示
ケース1
入力Trace
Return
ケース2
Trace
Return
最小二乗法(1次式)の拡張 相関係数と95%信頼区間コード表示 コード表示
ケース1
入力Trace
Return
ケース2
Trace
Return
最小二乗法(n次式)y = a[0] + a[1]x + … + a[n]*xn の a[i] を求めるコード表示 コード表示
n次式、2 +・・・+a[n]xn
a[0] a[1] a[2] ・・・ a[n] 定数項 n ∑x ∑x2 ・・・ ∑xn ∑y ∑x1 ∑x2 ∑x3 ・・・ ∑xn+1 ∑yx ∑x2 ∑x3 ∑x4 ・・・ ∑xn+2 ∑yx2 : : : : : : ∑xn ∑xn+1 ∑xn+2 ・・・ ∑x2n ∑yxn
ケース1
入力2 Trace
Return
ケース2
Trace
Return
最小二乗法(多項式)y = a[0] + a[1]x[0] + … + a[n]*x[n-1] の a[i] を求めるコード表示 コード表示
多項一次式
a[0] a[1] a[2] ・・・ a[n] 定数項 n ∑x[0] ∑x[1] ・・・ ∑x[n-1] ∑y ∑x[0] ∑x[0]x[0] ∑x[0]x[1] ・・・ ∑x[0]x[n-1] ∑yx[0] ∑x[1] ∑x[1]x[0] ∑x[1]x[1] ・・・ ∑x[1]x[n-1] ∑yx[1] : : : : : : ∑x[n-1] ∑x[n-1]x[0] ∑x[n-1]x[1] ・・・ ∑x[n-1]x[n-1] ∑yx[n-1]
ケース1
入力Trace
Return
ケース2
Trace
Return
多点系 補間法
ニュートンの補間法コード表示 コード表示
n+1個の点(x0 ,y0 ), (x1 ,y1 ), …,(xn ,yn )を通るn次式 f(x)を、0 + c1 (x-x0 ) + c2 (x-x0 )(x-x1 )
+ … + cn (x-x0 )(x-x1 )…(x-xn-1 )0 )=y0 、f(x1 )=y1 、…、f(xn+1 )=yn+1 「ニュートンの補間公式」
その式に、x=px に対応する y の値 py を戻します。
ケース1
入力Trace
Return
ケース2
Trace実行
Return実行
ラグランジュの補間法コード表示 コード表示
n+1組の点xa[0]~xa[n]、ya[0]~ya[n] を通るn次式をラグランジュの補間法により求め、m 個の、xa[n+1]~xa[n+1} における ya[n+1]~ya[n+m] を戻します。
n次式に一般化して、0 y0 +c1 y1 +c2 y2 +・・・+cn yn k は、次の式になります。
ck = (x-x0 )/(xk -x0 ) * (x-x1 )/(xk -x1 ) * … * (x-xk-1 )/(xk -xk-1 )k )/(xk -xk )の項がないことに注意)k+1 )/(xk -xk+1 ) * … * (x-xn )/(xk -xn ) 「ラグランジュの補間法」
ケース1
入力Trace実行
Return実行
ケース2
Trace実行
Return実行
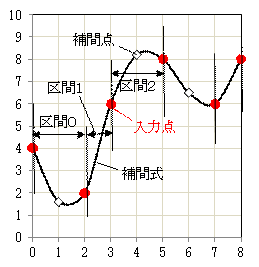
スプライン補間(3次)コード表示 コード表示
スプライン補間は、n+1個の点 (x0 ,y0 ), (x1 ,y1 ), … , (xn ,yn ) を、2つの点の区間 [xj ~xj+1 ]ごとに別々の式(一般には3次式)Sj (x) を設定して緩やかな曲線にし、極端な補間値にならないようにする補間法です。参照:「スプライン補間」
区間 [xj ~xj+1 ] における3次式をj =aj (x-xj )3 + bj (x-xj )2 + cj (x-xj ) + dj (j=0~n-1) j , bj , cj , dj を求めることになります。
これらの3次式が滑らかにつながっている必要があります。それで、xj におけるSj-1 とSj の1次導関数(傾き)S(1) と2次導関数(滑らかさ)S(2) の値が等しいという条件を加えます。さらに、始点 x0 と終点 xn での2次導関数の値が0であるとの仮定をします。
ケース1
Trace実行
Return実行
ケース2
Trace実行
Return実行
最小二乗法(高次式)による補間コード表示 コード表示
n組の(x,y)から、最小二乗法により、r次の近似式 y=c0 +a1 x+c2 x2 +...+cr xr の係数 ci を求め。この近似式により、f個の px に対応する py を計算します。; ソースコード 「回帰分析・最小二乗法」 、
「多項式、高次式での最小二乗法」
ケース1
入力2 - 0.046 x3 Trace実行
Return実行
ケース2
Trace実行
Return実行
ベジェ曲線(2次、3次)コード表示
ベジェ曲線とは、始点と終点を固定し、その直線を制御点から引っ張るような曲線にしたものです。2 *x[0] + 2(1-t)t*x[1] + t2 *x[2]2 *y[0] + 2(1-t)t*y[1] + t2 *y[2]3 *x[0] + 3(1-t)2 t*x[1] + 3(1-t)*t2 *x[2] + t3 *x[3]3 *y[0] + 3(1-t)2 t*y[1] + 3(1-t)*t2 *y[2] + t3 *y[3]
ケース1
始点 制御点 終点実行 ケース2
実行
正方行列系 線形連立方程式など
連立一次方程式(ガウス=ジョルダンの掃出し法)コード表示 コード表示
説明変数や被説明変数の標本から、連立方程式の定式化を行い、解を求めるまでの一連の処理を行うには、
maMregEq 関数があります。
ケース1
入力0 + 3x1 + 2x2 = 120 + 4x1 + 0x2 = 100 + 1x1 + 5x2 = 20Trace実行
Return実行
ケース2
Trace実行
Return実行
naTdma 三重対角行列の連立方程式コード表示 コード表示
三重対角行列とは、下図の左行列のように、対角線とその左右要素以外の要素が0である行列です。右のd行列を定数項としたときの解xを求めます。
三重対角行列はゼロ要素が多く、入力データを行列形式で与えるのは非効率ですので、ここでは次の形式で与えることにします。0 , a1 , …, an-1 ]0 , b1 , …, bn-1 ]0 , c1 , …, cn-1 ]0 , d1 , …, bn-1 ]0 とcn-1 は不要なのですが、形式を整えるために、任意の値(0)を与えることにします。)
ケース1
モデル0 , 2, 1. 3, 3];0 ];Trace
Return
ケース2
Trace
Return
N+1個の点を通るN次式の係数コード表示 コード表示
例えば、4(=N+1)個の点 [x0,y0], [x1,y1], [x2,y2], [x3,y3] を通る3(=N)次式2 + c[3] x3 n が極端に大きくならないように単位を調整してください。
ケース1
入力2 - 1 x3 Trace
Return
ケース2
Trace実行
Return実行


 入力
入力