補間（スプライン）

スプライン補間とは

補間に関する基本概念は「補間」を参照してください。
　そこで紹介したラグランジュの補間公式やニュートンの補間公式は、与えられたｎ＋１の点を通る唯一のｎ次式を求めることがポイントでした。そのため、次数が高くなると、極端な補間値になってしまうことがあります。

スプライン補間は、ｎ＋１個の点 (x₀,y₀), (x₁,y₁), … , (x_n,y_n) を、２つの点の区間 [x_j～x_j+1]ごとに別々の式（一般には３次式）Ｓ_j(x) を設定して緩やかな曲線にし、極端な補間値にならないようにする補間法です。計算はかなり複雑になります。

定式化

区間 [x_j～x_j+1] における３次式を
　　Ｓ_j＝a_j(x-x_j)³ + b_j(x-x_j)² + c_j(x-x_j) + d_j　　　(j=0～n-1)
とします。
　これらの３次式が滑らかにつながっている必要があります。それで、x_j におけるＳ_j-1とＳ_jの１次導関数（傾き）Ｓ⁽¹⁾ と２次導関数（滑らかさ）Ｓ⁽²⁾ の値が等しいという条件を加えます。さらに、始点 x₀ と終点 x_n での２次導関数の値が０であるとの仮定をします。

決定すべき件数 a_j, b_j, c_j, d_j の個数は４ｎ個です。
　それに対して、上の条件を満たす方程式は、次の４ｎ個になりますので、連立方程式を解くことにより、各係数の値を決定することができます。

• 条件Ａ：Ｓ_j が点 (x_j,y_j) を通ることから、
  d_j＝y_j　　　（j=0～n-1 の n個の式）
  
• 条件Ｂ：Ｓ_j が点 (x_j+1,y_j+1)を通ることから、
  a_j(x_j+1-x_j)³ + b_j(x_j+1-x_j)² + c_j(x_j+1-x_j) + d_j ＝ y_j+1 　　　（j=0～n-1 の n個の式）
• 条件Ｃ：x_j における左右の１次導関数の値が等しいことから、
  Ｓ⁽¹⁾_j-1(x_j)＝Ｓ⁽¹⁾_j(x_j)
  3a_j-1(x_j-x_j-1)² + 2b_j-1(x_j-x_j-1) + c_j-1＝c_j　　　（j=1～n-1 の n-1個の式）
• 条件Ｄ：x_j における左右の２次導関数の値が等しいことから、
  Ｓ⁽²⁾_j-1(x_j)＝Ｓ⁽²⁾_j(x_j)
  6a_j-1(x_j-x_j-1) + 2b_j-1＝2b_j　　　（j=1～n-1 の n-1個の式）
• 条件Ｅ：始点 x₀ と終点 x_n での２次導関数の値が０であることから、
  6a₀x₀ + 2b₀＝0,　6a_n-1x_n + 2b_n-1＝0　　（2個の式)

連立方程式

上の関係に、x_j, y_j の値を代入して連立方程式にすればよいのでが、複雑なので、次のように変形して解く方法がとられます。この変形過程はここでの目的ではないので、結果だけを示します。
　　u_j＝2b_j 　(j=1～n-1）
　　　　(u₀＝0, u_n＝0 とする）
　　h_j＝x_j+1 - x_j　　(j=0～n-1）
　　v_j＝6( (y_j+1-y_j)/h_j - (y_j-y_j-1)/h_j-1)　　(j=1～n-1)
と置換すると、u_j を求める連立方程式は、次のようになります。変数側の要素がすべてｘの差の1次式になっていること、対角線とその両側にだけ値を持つ（それ以外は０）である特徴があります。

　 u₁　　　u₂　　　u₃　　 …　u_j-1　　 u_j　　 u_j+1　… u_n-2　　　u_n-1
2(h₀+h₁)　 h₁　　　　　　　　　　　　　　　　　　　　　　　　　　　　　＝ v₁
　 h₁　 2(h₁+h₂)　 h₂　　　　　　　　　　　　　　　　　　　　　　　　　＝ v₂
　　　　　 h₂　 2(h₂+h₃)　h₃　　　　　　　　　　　　　　　　　　　　　 ＝ v₃
　　　　　　　　　　　　 :::　　　　　　　　　　　　　　　　　　　　　　　:
　　　　　　　　　　　　　　 h_j-1　2(h_j-1+h_j)　h_j　　　　　　　　　　　 ＝ v_j
　　　　　　　　　　　　　　　　　　　　　　　　 :::　　　　　　　　　　 ：
　　　　　　　　　　　　　　　　　　　　　　　　　　 h_n-2　2(h_n-2+h_n-1) ＝ v_n-1

各係数への復元

条件Ａより、d_j＝y_j は直ちに求められます。
　連立方程式を解いて、u_jが求まれば、
　b_j＝(1/2)*u_j で計算できます。
　c_jは、かなりの式操作がありますが、
　　c_j＝(y_j+1-y_j)/(x_j+1-x_j) - (1/6)*(2u_j+u_j+1)*(x_j+1-x_j)
から計算できます。
　a_j は、条件Ｄから
　　6a_j(x_j+1-x_j) + 2b_j＝2b_j+1
　　∴　a_j＝(1/6)*(u_j+1-u_j)/(x_j+1-x_j)
から計算できます。

数値例

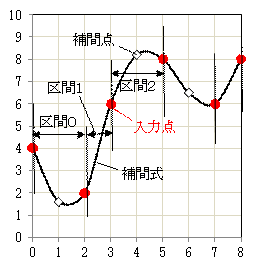
次の６点(n=5)（このページの先頭にあるグラフの赤点）を入力とする補間式を考えます。
　　j 　　　０　　　１　　　２　　　３　　　４　　　５
　　x_j　　　０　　　２　　　３　　　５　　　７　　　８
　　y_j　　　４　　　２　　　６　　　８　　　６　　　８
　h_j＝x_j+1-x_j, v_j＝6( (y_j+1-y_j)/h_j - (y_j-y_j-1)/h_j-1) を計算して付け加えます。
　　h_j　　　２　　　１　　　２　　　２　　　１
　　v_j　　　　　　３０　　－１８　－１２　１８

これより、左の連立方程式が作られ、右の解が得られます。
　　u₁　　u₂　　u₃　　u₄　　　　　　　　　　解
　　６　　１　　　　　　　＝　３０　　　　u₁＝ 5.5702
　　１　　６　　２　　　　＝－１８　　　　u₂＝-3.4212
　　　　　２　　８　　２　＝－１２　　　　u₃＝-1.5215
　　　　　　　　２　　６　＝　１８　　　　u₄＝ 3.5072

次の逆変換により、係数 a_j, b_j, c_j, d_j が得られます。
　　a_j＝(1/6)*(u_j+1-u_j)/(x_j+1-x_j)
　　b_j＝(1/2)*u_j
　　c_j＝(y_j+1-y_j)/(x_j+1-x_j) - (1/6)*(2u_j+u_j+1)*(x_j+1-x_j)
　　d_j＝y_j

その結果、区間ごとの補間式は次のようになります。
　ｊ　区間　　　a_j　　　　　　b_j　　　　　c_j　　　　　d_j
　０　0～2：　0.4642(x-0)³ +0　　(x-0)² -2.853(x-0) + 4
　１　2～3： -1.4990(x-2)³ +2.785(x-2)² +2.713(x-2) + 2
　２　3～5：　0.1583(x-3)³ -1.711(x-3)² +3.788(x-3) + 6
　３　5～7：　0.4191(x-5)³ -0.761(x-5)² -1.155(x-5) + 8
　４　7～8： -0.5845(x-7)³ +1.754(x-7)² +0.833(x-7) + 6
これらをつなぐと上のグラフの曲線になり、赤点近傍で滑らかに接続しています。

この補間式で、x=1, 4, 6 のときの y を計算すると次のようになり、グラフの◇の点になります。
　　x=1：　0.4642(1-0)³ +0　　(1-0)² -2.853(1-0) + 4＝ 1.607
　　x=4：　0.1583(4-3)³ -1.711(4-3)² +3.788(4-3) + 6＝ 8.236
　　x=6：　0.4191(6-5)³ -0.761(6-5)² -1.155(6-5) + 8＝ 6.504

計算プログラム