定積分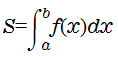（台形則、シンプソン則）

定積分を求める代表的な方法である台形則とシンプソン則を説明します。

長方形近似

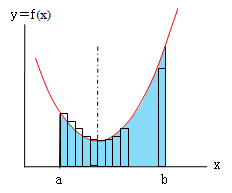
左図の青色の部分の面積を求めるには、図のような長方形で近似するのが最も簡単です。
閉区間［ａ，ｂ］をｎ等分して、ｘ₀(=a),ｘ₁,ｘ₂,....,ｘ_n(=b)の点とします。その幅（微小区間）ｈは、ｈ＝(ｂ－ａ)／ｎになります。
y_i＝ｆ(ｘ_i)とすれば、その長方形の面積ΔＳ_iは、ΔＳ_i＝y_iｈですから、求める積分の値Ｓは、
　　　　　　　　　ｂ－ａ
　　　Ｓ＝∑y_iｈ＝───（ｙ₀＋ｙ₁＋ｙ₂＋....＋ｙ_n-1）
　　　　　　　　　　ｎ
となります。

しかしこれでは、あまりよい近似にはならないのは明らかです。それで、曲線ｙ＝ｆ(x)を微小区間で一次式（台形則）や二次式（シンプソン則）で近似するのです。

台形則

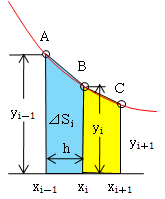
台形則では、微小区間を右図の青色の部分のように台形にします。
　このとき、ΔＳ_iは、
　　　ΔＳ_i＝（ｈ／２）×（ｙ_i-1＋ｙ_i）
となります。
　両端を考慮すれば、定積分Ｓは、
　　　　　ｂ－ａ　ｙ₀＋ｙ_n
　　　Ｓ＝───（────＋ｙ₁＋ｙ₂＋....＋ｙ_n-1）
　　　　　　ｎ　　　 ２
となります。

長方形近似と比較すると、長方形近似ではｙ₀をそのまま加え、ｙ_nを無視しているのに対して、台形則では、その２つの平均をとっています。それだけの違いだということになります。

シンプソン則

シンプソン則は、上右図のＡ、Ｂ、Ｃ点を２次式で近似します。
　中間の説明は省略しますが、ここでは閉区間［a，b］を２ｎ等分して、ｈ＝(ｂ－ａ)／２にすると（すなわち、 、ｘ₀(=a),ｘ₁,ｘ₂,....,ｘ_2n(=b)とすると、
　　　　　ｂ－ａ
　　　Ｓ＝───｛（ｙ₀＋ｙ_2n)＋４(ｙ₁＋ｙ₃＋...ｙ_2n-1)＋２(ｙ₂＋ｙ₄＋...ｙ_2n-2)｝
　　　　　 ６ｎ
となります。

数値例

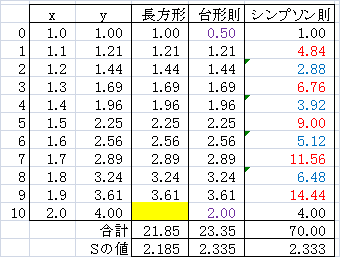
たとえば、右図のように、閉区間［１，２］を１０等分した（ｎ＝１０（シンプソン則では２ｎ＝１０）、ｈ＝０.１）ｘとｙの値が与えられているとします。

長方形近似

合計は、ｙ₀＋ｙ₁＋ｙ₂＋....＋ｙ_n-1＝２１.８５です。最後のｘ_n（黄色の要素）は計算から除外します。
(ｂ－ａ)/ｎ＝０.１ですから、Ｓ＝０.１×２１.８５＝２.１８５になります。

台形則

ｙ₀とｙ_nを１／２にしています（紫の要素）。それ以外は長方形近似と同じです。

シンプソン則

赤の要素を４倍、青の要素を２倍して合計７０.００を算出しています。
２ｎ＝１０なのですから、（ｂ－ａ)／６ｎ＝１／３０になります。Ｓ＝７０／３０＝２.３３３になります。

実は、このデータは、ｙ＝ｘ²から算出したものです。
　　
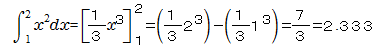
長方形近似→台形則→シンプソン則の順序で近似がよくなっていることがわかります。しかも、データが２次式からとったものなので、シンプソン則では真の値に一致しています。

数値積分の計算プログラム