方程式の根（二分法、ニュートン法）

方程式 ｆ(x)＝０ の根を求める代表的な方法である二分法とニュートン法（ニュートン－ラフソン法）を説明します。
　双方とも、１つの実根を求める方法で、その根の大体の値を知っていることが前提になります。

二分法

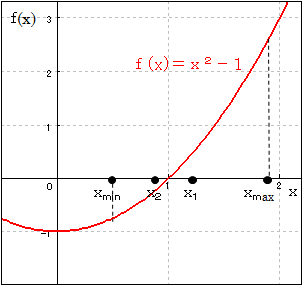
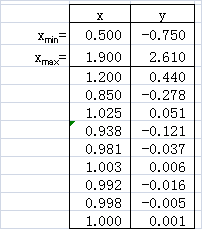
方程式 ｘ²－１＝０ の根のうち、ｘ＝１ を求めることを例にします。

ステップ１
　ｆ(x)＝ｘ²－１ のグラフは上左図のようになるので、おそらく ｘ_min＝０.５～ｘ_max＝１.９ の間に唯一の根があるだろうと想定できます。
　このように、ｆ(x)の値が、一方では正、一方では負になり、その間に根が１つだけしかない２点、ｘ_minとｘ_maxを与えます（この場合は、グラフが右上がりなので、ｆ(ｘ_min)＜０、ｆ(ｘ_max)＞０になりますが、右下がりの場合は、ｆ(ｘ_min)＞０、ｆ(ｘ_max)＜０となるように与えます）。

ステップ２
　ｘ_minとｘ_maxの中点 ｘ₁＝（ｘ_min＋ｘ₁）／２ を求めます。

ステップ３

• ｆ(ｘ₁) が０に非常に近いならば、ｘ₁が求める根ですので、計算を打ち切ります。
• ｆ(ｘ₁)＞０ならば、根はｘ₁よりも小さいので、ｘ₁をｘ_maxにして、ステップ２を行います。
• ｆ(ｘ₁)＜０ならば、根はｘ₁よりも大きいので、ｘ₁をｘ_minにして、ステップ２を行います。

ニュートン法

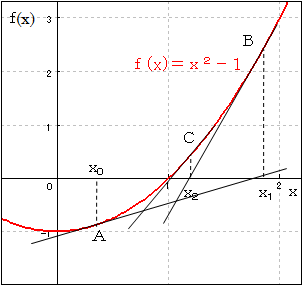
方程式 ｘ²－１＝０ の根のうち、ｘ＝１ を求めることを例にします。

ステップ１
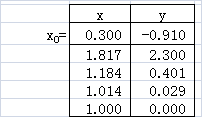
　ｆ(x)＝ｘ²－１ のグラフは上左図のようになるので、おそらく ｘ₀＝０.３ の近傍に根があるだろうと想定できます。
このように、ニュートン法では、根の近傍の値を初期値ｘ₀として与えます。

ステップ２
　ｘ₀に対応する点Ａにおける切線を引きます。その切線がｘ軸と交わる点をｘ₁とします。
　さらに、ｘ₁に対応する点Ｂにおける切線がｘ軸と交わる点をｘ₂として、ｘ₂に対応する点Ｂにおける切線を・・・と繰り返していく間に、根に近づきます。

その経過を上右表に示しました。ニュートン法は、二分法と比較して計算が面倒ですが、解に達するまでの繰り返し回数が少なくなります。

●ニュートン法の数学的説明
　ニュートン法は、方程式ｆ(x)と、その微分の式を与える必要があります。
　ｆ(x)の微分をｇ(x)とします（ｆ(x)＝ｘ²－１のとき、ｇ(x)＝２ｘになります）。
点Ａでの接線の勾配は、ｇ(ｘ₀)ですから、接線は
　　　ｙ＝ｇ(ｘ₀)（ｘ－ｘ₀）＋ｆ(ｘ₀)
となります。
それで、ｘ軸との交点ｘ₁は、
　　　ｘ₁＝ｘ₀－ｆ(ｘ₀)／ｇ(ｘ₀)
となります。一般的には、
　　　ｘ_i+1＝ｘ_i－ｆ(ｘ_i)／ｇ(ｘ_i)
として計算できます。

計算プログラム