例えば、毎年(xi)の売上高(yi)のようなデータがあるとき、xを説明変数、yを目的変数といいます。そして、y=Ax+Bとしたときの、A、Bを回帰係数といいます。
回帰分析とは、 説明変数と目的変数の関係を推定する統計的手法です。なお、説明変数が2つ以上あるとき重回帰分析といいます。
最小二乗法とは、回帰係数を求める手法です。
εi=Axi+B-yi
としたとき、
∑εi2→最小
となるようなAとBを求める手法です。
定式化

∑(Axi+B-yi)2
を最小にするために、
Bについて微分して0とすると、
Bn+AΣxi=∑yi
Aについて微分して0とすると、
BΣxi+A∑xi2=∑xiyi
となります。この連立方程式を解くと、A、Bが得られます。
数値例
次の5つのデータを用います。
xi yi xi2 xiyi
1 10 1 10
2 20 4 40
3 20 9 60
4 30 16 120
5 40 25 200
15 120 55 430
すると、上の連立方程式は
5B+15A=120
15B+55A=430
これを解くと、
A=7
B=3
となります。
なお、このy=7x+3の式に、x=6を代入するとy=7×6+3=45になります。
このように、最小二乗法を予測に用いることが多いのです。
→発展:「最小二乗法(多項式、高次式)」(stat-saisyo-jijoho2)
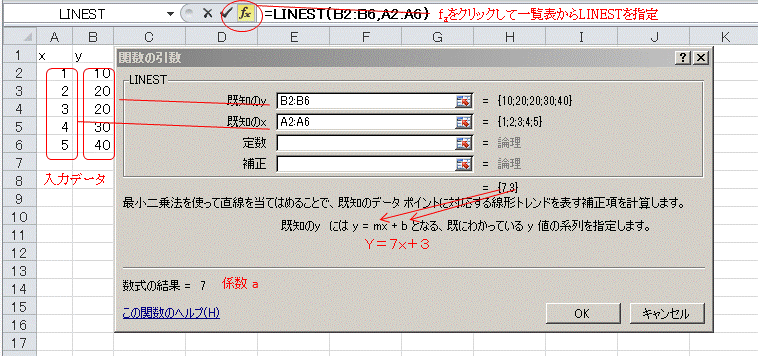
Excelによる計算
データを入力して、関数[fx]をクリックすると関数の一覧表が表示されるので、LINEST を指定すると図が表示されます。