待ち行列の概念
待ち行列とは
お店のレジを考えましょう。客がレジに到着し支払をして(これを「サービスを受ける」といいます)去っていきます。到着したときにレジが空いていれば,待たずにサービスを受けられますが,サービス中の人がいる場合には,自分の番がくるまで待ちますので行列ができます。待ち行列の理論(Queing Theory)とは,このような系について,待たないでサービスを受ける確率,行列の平均長さ,到着してから去るまでの平均時間などを計算する理論です。
待ち行列には,次のように多様な例があります。
客 窓口
- --
客 受付窓口
患者 診療
自動車 有料道路料金所
機械故障 修理工
処理要求 ホストコンピュータ
電話の送信 電話の受信(お話中)
待ち行列と到着・サービス分布の関係
客が平均5分おきに到着し,レジは平均3分かかるとします。もし,客の到着間隔とレジのサービス時間が一定であれば,待ちが生じることはありません。
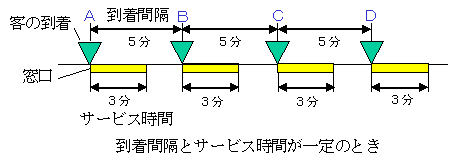
しかし,実際には客の到着は平均5分であっても,3分,8分,4分というようにバラツキがありますし,レジのサービス時間も平均は3分だとしても,それより短いこともあれば,長くかかることもあります。そのときには,下図のように待ちが生じます。
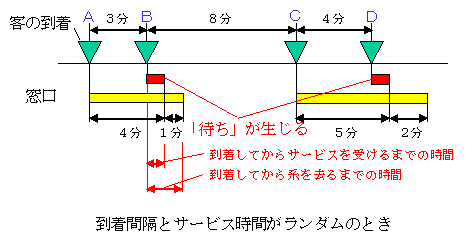
もし,到着やサービスの時間間隔が平均では5分と3分であるが,その分布がデタラメ(ランダムといいます)である(「ポアソン到着,指数サービス」といいます)したとき,理論的な計算をしますと,サービスを待っている人の平均値Lqは0.9人であり,到着してからサービスを受けるまでの平均待ち時間Wqは4.5分になります。平均サービス時間が4.5分ならば,Lq=8.1人,Wq=40.5分にもなってしまいます。
このように,直感とはかなり異なる状況になるのです。このようなことを計画時に知らずに設備投資をすると,実施してから多くのトラブルを生じる危険があります。待ち行列の知識が必要になるのです。
待ち行列で用いる記号
待ち行列では,次の記号をよく用います。
λ(ラムダ):客の平均到着率[人/時]⇔1/λ:客の平均到着間隔[時/人]
μ(ミュー):一つの窓口の平均サービス率[人/時]⇔1/μ:窓口の平均サービス時間[時/人]
s:窓口の個数
ρ(ロー)=λ/(sμ) 窓口が1個のときは ρ=λ/μ
P0:サービス中を含む(「系の中」という)客数が0である確率
(窓口が1個のときは,待たずにサービスが受けられる確率)
Pn:系の中の客数がn人である確率
L:系の中にいる客の平均人数[人]=1P1+2P2+3P3+・・・+nPn
Lq:サービスを待っている人の平均人数[人]=1Ps+1+2Ps+2+3Ps+3+・・・+(n-s)Pn
W:系の中(到着してからサービスを受けて去るまで)の平均時間[時]
Wq:到着してからサービスを受けるまでの平均待ち時間[時]
ポアソン分布と指数分布
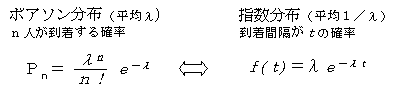
客の到着が単位時間あたり平均λでランダムに発生するとき,平均がλのポアソン分布になり,ある客が到着してから次の客が到着するまでの時間の間隔は平均1/λの指数分布になります。すなわち,ポアソン分布と指数分布は裏返しの関係があるのです。
ランダムとは
ランダムとはデタラメ(=法則性がない)のことですが,数学的には次の3つの仮定が可能であることをいいます。
- 独立性
- ある単位時間に到着する客の数は,それ以前の客の到着状況とは無関係だという性質です。先に大勢来たから今度は少ないだろうとか,これまでに増加しているのでもっと増えるだろうというような,以前の影響は受けないということです。
- 定常性
- 朝や夕方のアッシュアワーのような時間帯による変化はなく,到着の分布は常に一定であるという性質です。系の中にいる人数がn人である確率Pnは,時間によらず一定になります。
- 稀少性
- 単純にいえば,客は連れ立って来ることはなく,一人ずつ来るということです。いいかえれば,到着間隔は0にはならないということです。
ポアソン分布
単位時間内に一人の客が来る確率をpとすれば,来ない確率は(1-p)です。客の総数がN人であり,そのうちのn人が来るとすれば,その確率Pnは,
Pn=NCnpn(1-p)N-n
の二項分布になります。このとき,Np=λとして,Nを大きくすると,
Pn=(λn/n!)×e-λ
n! (nの階乗)=1×2×3×・・・×n, e (自然対数の底)=2.71828
に近づきます。これをポアソン分布といいます。このポアソン分布の平均はλ,分散もλです。
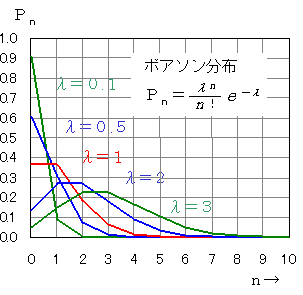
ポアソン分布のグラフを示します。n=4のとき,λ=2のグラフのPn,すなわちP2はほぼ0.1になります。これは,単位時間に到着する平均が2のとき,単位時間に4人が到着する確率が0.1であるということです。
各曲線がn=λ付近で最大になるのは,実際に到着する人数は平均に近いことが多いということですし,λが大きくなるほど平らになるのは,平均人数が多いほど実際に来る人数のバラツキが大きくなるからです。これは常識と一致しますね。
指数分布
到着間隔がtだということは,「t時間までには来なかった」ことと「t時に客が1人来た」ことのどちらかが起こるということです。tにおける確率をf(t) とすれば,「t時に客が1人来た」確率はf(t)/λであり,「t時間までには来なかった」のはf(t) の0~tまでの積分になりますから,
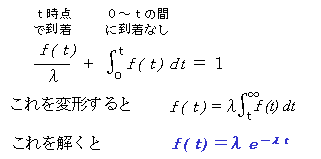
が成立します。これを指数分布といます。
指数分布の平均は1/λ,分散は1/λ2です。
このf(t)をtから∞まで積分すると,e-λtになります。これは,到着間隔がtよりも大きいときの確率になります。このグラフは下のようになります。
λtが1.6のときの確率は0.2になります。これは実際の到着t=1.6/λ[時]以上である確率が0.2であるということです。仮にλを2[人/時](平均到着間隔は1/2[時/人])としましょう。すると,t=1.6/2=0.8[時]であり,これは平均到着間隔の1.6倍です。すなわち,このグラフの横軸は平均到着間隔の倍数と考えてよいのです。
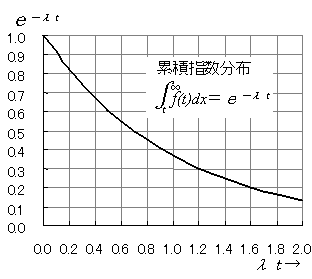
なおここまでは,説明をしやすいために,客の到着を例にしましたが,窓口のサービスについても同様です。平均サービス率がμのときは次のようになります。
| 事象 | 分布の種類 | 式 | 平均 | 分散 |
| サービス完了回数 | ポアソン分布 | Pn=(μn/n!)×e-μ | μ | μ |
|---|---|---|---|---|
| サービス時間の分布 | 指数分布 | f(t)= μe-μt | 1/μ | 1/μ2 |
アーラン分布(M/Ek/1)
実務では,一定分布になることは稀ですし,指数分布のようにt=0のときが最大になることも少ないでしょう。指数分布と一様分布との中間に相当する分布にアーラン分布があります。kをパラメタ(位相)として,次式で表されます。
f(t)={(μt)k-1/(k-1)!}×μe-μt
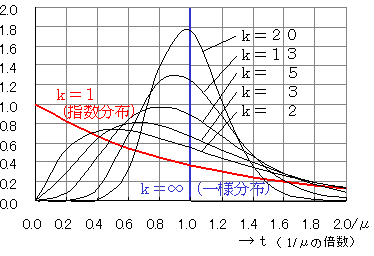
上式で,k=1とすると,{ }の中が1になり,指数分布と一致します。また,k=∞のときは,f(t)=1/μになり,一様分布と一致します。アーラン分布をイメージ的に解釈すると(客の到着では)k人おきの客を対象としたことになります。
なお,kを変化させたときのグラフは,次のようになります。
アーラン分布の平均は 1/μ,分散は 1/kμ2 になります。
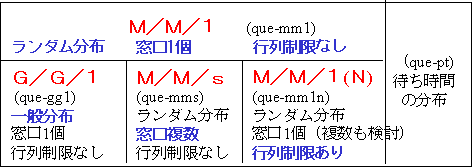
待ち時間の分類(ケンドールの記号)
ケンドール(Kendall)は,待ち行列を次のように分類しました。これをケンドールの記号といいます。到着・サービスの分布,窓口の個数,行列の制限有無により分類しています。なお,この他にも,客の優先順位による区分が考えられますが,ここではすべて先着順とします。

リトルの公式
上記のような分類により多くの関係式がありますが,ほとんどの場合には次の式が成立しますので,L,Lq,W,Wqのいずれか1つを知れば,他の3つは簡単に求めることができます。これをリトルの公式といいます。
L=Lq+λ/μ
Wq=Lq/λ
W=Wq+1/μ
このシリーズの目次
このシリーズでは,次のケースについて検討します。
最も基本的なものはM/M/1で、これは初級レベルの情報技術者試験でも出題されています。他のモデルは、私たちのレベルを越えますが、実社会ではむしろ一般的です。イメージを理解してもらうために掲げました。
単一窓口
- M/M/1(or-que-mm1)
- 待ち行列での最も代表的なケースです。窓口が1個で,客の到着分布,窓口のサービス分布がランダム(すなわち,ポアソン到着・指数サービス)であり,客の行列の長さに制限がない場合を取扱います。
P0=1-ρ
Pn=ρnP0=ρn(1-ρ)
L=ρ/(1-ρ)
Lq=ρ2/(1-ρ)
W=L/λ=1/(μ-λ)
Wq=Lq/λ=λ/(μ(μ-λ)) - G/G/1(or-que-gg1)
- M/M/1では,その分布がランダム分布の場合でした。これを「ポアソン到着,指数分布」といいますが,ポアソン分布,指数分布について説明します。
また,到着やサービスの分布により,LやWに大きな違いが出ることは,先に示しました。ここでは分布が,一定分布であるとき,アーラン分布(ランダム分布と一定分布の中間的な分布)のときについて考えます。 - M/M/1(N)(or-que-mm1n)
- 行列の長さに制限があるケースです。ここまでは,行列の長さの制限はなく到着した客はかならずサービスを受けるまで待っているケースでした。ところが,駐車場のように行列に制限があるとか,長い行列があれば並ばずに去ることもあります。また,電話のお話中のように,行列そのものが存在できないこともあります。
複数窓口
- M/M/s(or-que-mms)
- 窓口が複数のケースです。平均サービス率が2μである窓口が1個の場合とμの窓口が2個の場合では,LやWに大きな違いがあります。これは1台の高性能設備で集中するか,複数の低性能設備に分散するかなどの検討に用いられます。
- 待ち時間の分布(or-que-pt)
- これまでは,主にLやWqなどの平均値を取扱ってきましたが,顧客の観点からは,平均待ち時間よりも,長く待つことがどれだけあるのかという尺度のほうが適切でしょう。ここでは,M/M/1およびM/M/Sについて,到着してからサービスを受けるまでの時間の分布について考えます。
- プログラム(or-que-program)
- M/M/s型の計算プログラム
- 図表(or-que-chart)
- M/M/s型の計算図表
シミュレーション
待ち行列を検討する現実の対象は複雑なので、これらの理論的な公式を単純に適用できないことが多くあります。そのような対象には、複雑な定式化を考えるよりも、現実のプロセスをモデル化して、机上実験するほうが適切です。
そのようなアプローチをシミュレーションといい、ORの大きな分野になっています。これに関しては、別章「シミュレーション」を参照してください。