スタートページ> Web教材一覧> オペレーションズリサーチ> 待ち行列
M/M/s型は,M/M/1型の窓口数を複数(s個)にしたものです。それだけのことですが,式は非常に複雑になります。
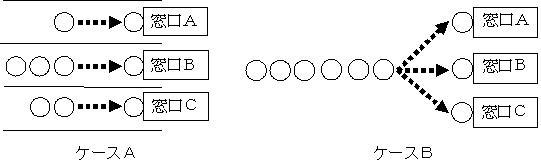
複数窓口といっても,下のケースAのように窓口別に行列する場合は,それぞれの窓口についてM/M/1の公式が成立します。ここで取扱うM/M/s型はケースBのような場合です。

このとき,単にM/M/1の公式で平均サービス率μが3倍にしたのではいけません。ケースAのときには,窓口Aが空いていても窓口Bに並んでいる人はサービスが受けられませんが,ケースBのときには,どの窓口でも空いている窓口があればサービスが受けられます。直感的にもケースBのほうが効率的だと考えられます。
状態方程式は,次のようになります。(ここでは,ρ=λ/sμになります)
λP0=μP1
λPn-1+(n+1)μPn+1=(λ+nμ)Pn
λPn-1+sμPn+1=(λ+sμ)Pn
これより,次の式が得られます。

それにしても,あまりにもゴツイですね。
上の公式に窓口数s=1~3を代入して整理すると,次の表が得られます。
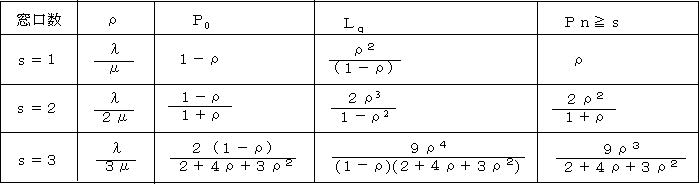
複数窓口(s個)で行列に制限がある(N人)とき,すなわちM/M/s(N)のときを考えます。次のようにかなり複雑なものになりますが,N=sのときは比較的簡単になります。

N=sの場合は,代表電話番号で受ける電話が数台あるようなとき,あるいは電話局での回線の容量を考える場合など,通信では重要なケースであり,上のPsはアーランB式と呼ばれでいます。
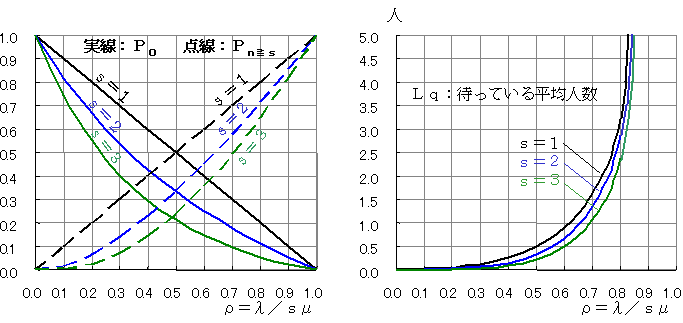
アーランB式のグラフは下のようになります。同じρであっても,窓口数sが増加するにつれて,窓口がふさがっている確率は小さくなり,サービスを受けられる確率が増大することがわかります。

たとえば,1回の電話では平均3分話をする(μ=1/3)として,平均1分おきにかかってくる(λ=1/2)ならば,λ/μ=3になります。もし受信用の電話が2台ある(s=2)ならば,ρ=3/2=1.5になり,上右図のs=2のグラフ()から,お話中である確率は0.53であることがわかります。
逆に,λ/μ=3のときに,0.9の確率でサービスが受けられるようにする(Ps=0.1)には,電話が何台必要かを考えましょう。
上左図からs=2ではρ=0.3になりますが,s=(λ/μ)/ρですからs=3/0.3=10となり,不足してしまいます。これを多様なsについて計算すると,
グラフからのρ (λ/μ)/ρからのs
s=3 0.42 7.1 不足
s=5 0.58 5.1 ほぼ一致
s=10 0.75 4.0 過剰
となるので,5台が答となります。
窓口の個数sを変化させたときのグラフは下のようになります。ρが同じなのに,窓口が多数になるにつれて,
Pn≧s:すべての窓口がふさがっている確率が小さくなる
→ すぐにサービスが受けられる確率が大きくなる
Lq:サービスを受けるまでの平均待ち時間が短くなる
ことがわかります。
客の平均到着率をλ=6,窓口1個の平均サービス率をμ=6として,窓口がs=2個ある場合を考えます。
ケースAの場合は,客はランダムにどちらかの窓口に並ぶとすれば,客の平均到着率λ=3として,M/M/1の公式を適用すればよいことになります。ρ=λ/μ=0.5で,s=1ですから,
上左図から,到着して待つ確率:Pn≧s=0.5
上右図から,サービスを受けるまでの平均待ち時間:Lq=0.5
が得られます。
ケースBの場合では,ρ=λ/sμ=6/(2・6)=0.5ですが,s=2ですので,
Pn≧s=0.33
Lq=0.33
となり,どちらもケースBのほうが効率がよいことがわかります。
ケースCとして,平均サービス率がμ=12の窓口を1個にする場合を考えます。この場合もρ=6/12=0.5で,s=1ですから,ケースAと同じになり,ケースBのほうが効率がよいことになります。
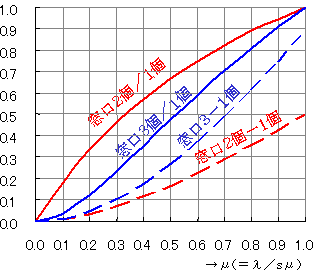
式を用いた一般的な考察をしましょう。(A)平均サービス率がsμの能力の窓口が1個のときと,(B)平均サービス率がμの能力の窓口がs個のときでは,ともにρ=λ/sμになりますが,Bのほうが効率がよくなりますが,たとえばs=2のときの,LqB/LqAの比を計算してみましょう。
AのLqA=ρ2/(1-ρ),BのLqB=2ρ3/(1-ρ2)ですから,
LqB/LqA={2ρ3/(1-ρ2)}/{ρ2/(1-ρ)}=2ρ/(1+ρ)
になります。このグラフは下の赤い実線になりますので,
LqB/LqA≦1 ∴ LqB≦LqA
となります。
LqAとLqBの差で比較するならば,
LqA-LqB={ρ2/(1-ρ)}-{2ρ3/(1-ρ2)}=ρ2/(1+ρ)≧0 ∴ LqB≦LqA
となり,同じ結果になります(当然!)。この差は赤い点線になります。
s=3についてもとになり,同様な結果になります。