ポアソン分布と指数分布
この部分は「待ち行列の概要」と重複します。
結論
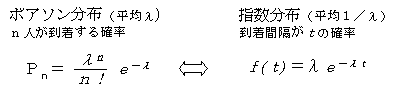
客の到着が単位時間あたり平均λでランダムに発生するとき,平均がλのポアソン分布になり,ある客が到着してから次の客が到着するまでの時間の間隔は平均1/λの指数分布になります。すなわち,ポアソン分布と指数分布は裏返しの関係があるのです。
ランダムとは
ランダムとはデタラメ(=法則性がない)のことですが,数学的には次の3つの仮定が可能であることをいいます。
- 独立性
- ある単位時間に到着する客の数は,それ以前の客の到着状況とは無関係だという性質です。先に大勢来たから今度は少ないだろうとか,これまでに増加しているのでもっと増えるだろうというような,以前の影響は受けないということです。
- 定常性
- 朝や夕方のアッシュアワーのような時間帯による変化はなく,到着の分布は常に一定であるという性質です。系の中にいる人数がn人である確率Pnは,時間によらず一定になります。
- 稀少性
- 単純にいえば,客は連れ立って来ることはなく,一人ずつ来るということです。いいかえれば,到着間隔は0にはならないということです。
ポアソン分布
単位時間内に一人の客が来る確率をpとすれば,来ない確率は(1-p)です。客の総数がN人であり,そのうちのn人が来るとすれば,その確率Pnは,
Pn=NCnpn(1-p)N-n
の二項分布になります。このとき,Np=λとして,Nを大きくすると,
Pn=(λn/n!)×e-λ
n! (nの階乗)=1×2×3×・・・×n, e (自然対数の底)=2.71828
に近づきます。これをポアソン分布といいます。このポアソン分布の平均はλ,分散もλです。
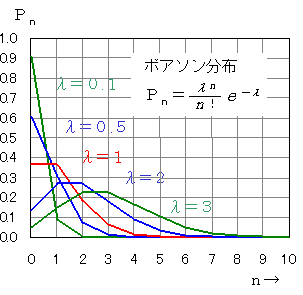
ポアソン分布のグラフを示します。n=4のとき,λ=2のグラフのPn,すなわちP2はほぼ0.1になります。これは,単位時間に到着する平均が2のとき,単位時間に4人が到着する確率が0.1であるということです。
各曲線がn=λ付近で最大になるのは,実際に到着する人数は平均に近いことが多いということですし,λが大きくなるほど平らになるのは,平均人数が多いほど実際に来る人数のバラツキが大きくなるからです。これは常識と一致しますね。
指数分布
到着間隔がtだということは,「t時間までには来なかった」ことと「t時に客が1人来た」ことのどちらかが起こるということです。tにおける確率をf(t) とすれば,「t時に客が1人来た」確率はf(t)/λであり,「t時間までには来なかった」のはf(t) の0~tまでの積分になりますから,
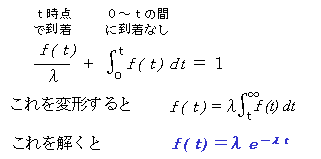
が成立します。これを指数分布といます。
指数分布の平均は1/λ,分散は1/λ2です。
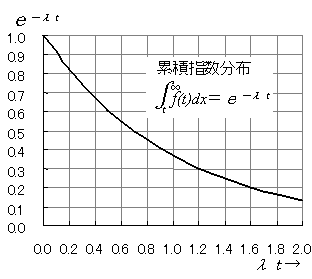
このf(t)をtから∞まで積分すると,e-λtになります。これは,到着間隔がtよりも大きいときの確率になります。このグラフは下のようになります。
λtが1.6のときの確率は0.2になります。これは実際の到着t=1.6/λ[時]以上である確率が0.2であるということです。仮にλを2[人/時](平均到着間隔は1/2[時/人])としましょう。すると,t=1.6/2=0.8[時]であり,これは平均到着間隔の1.6倍です。すなわち,このグラフの横軸は平均到着間隔の倍数と考えてよいのです。
なおここまでは,説明をしやすいために,客の到着を例にしましたが,窓口のサービスについても同様です。平均サービス率がμのときは次のようになります。
| 事象 | 分布の種類 | 式 | 平均 | 分散 |
| サービス完了回数 | ポアソン分布 | Pn=(μn/n!)×e-μ | μ | μ |
|---|---|---|---|---|
| サービス時間の分布 | 指数分布 | f(t)= μe-μt | 1/μ | 1/μ2 |
一定分布(M/D/1)
これは,サービス時間が一定値 1/μ である場合です。分散は0です。窓口の場合はレギュラーサービス,客の場合はレギュラー到着ともいいます。
アーラン分布(M/Ek/1)
実務では,一定分布になることは稀ですし,指数分布のようにt=0のときが最大になることも少ないでしょう。指数分布と一様分布との中間に相当する分布にアーラン分布があります。kをパラメタ(位相)として,次式で表されます。
f(t)={(μt)k-1/(k-1)!}×μe-μt
上式で,k=1とすると,{ }の中が1になり,指数分布と一致します。また,k=∞のときは,f(t)=1/μになり,一様分布と一致します。アーラン分布をイメージ的に解釈すると(客の到着では)k人おきの客を対象としたことになります。
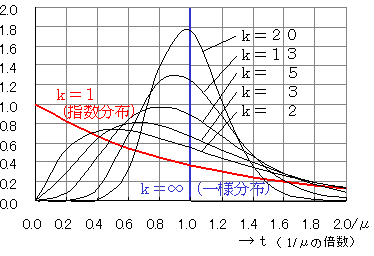
なお,kを変化させたときのグラフは,次のようになります。
アーラン分布の平均は 1/μ,分散は 1/kμ2 になります。
M/G/1でのWq(サービスが多様な場合の平均待ち時間)
客の到着は自由になりませんが,サービス時間のコントロールをすることは比較的可能です。それで,ポアソン到着でサービスが多様な分布のときの研究が広く行われています。ここでは,代表的なポラチェック・ヒンキンの公式の結果だけを示します。
Wq={λ/μ(μ-λ)}×{(1+C2)/2}
右辺の第1項は,M/M/1でのWqであり,サービス分布により第2項の補正係数がつくと理解すればよいでしょう。
ここでCはサービス時間の変動係数(=標準偏差/平均)であり,C2は分散/平均2になります。
各種分布での補正係数は次のようになります。すなわち,サービス時間が一定のときは,ランダムのときと比較して,平均待ち時間は1/2になります。作業の標準化が顧客満足を得る例であるともいえましょう。
| 分布 | 平均 | 分散 | C2 | (1+C2)/2 |
| 指数分布(M) | 1/μ | 1/μ2 | 1 | 1 |
|---|---|---|---|---|
| 一定分布(D) | 1/μ | 0 | 0 | 1/2 |
| アーラン分布(Ek) | 1/μ | 1/kμ2 | 1/k | (1+k)/2k |
なお,Wqがわかれば,リトルの公式により,W,Lq,Lを求めることができます。
W=Wq-1/μ, Lq=λWq, L=λW
G/G/1の近似式
到着が一般分布のときは,上のような正確な定式化はできず,近似式があるだけです。
Wq={λ/μ(μ-λ)}×{(Cλ2+Cμ2)/2}
ここで、{(Cλ2+Cμ2)/2}を補正係数とします。
Cλは客の到着の変動係数,Cμは窓口のサービスの変動係数
M/M/1のとき、補正係数=1です。
M/G/1への変形
客の到着分布は制御できないが、サービス時間分布はある程度は制御できるとしましょう。上のM/G/1をG/G/1の近似式から吟味します。
到着がポアソン分布では平均λ,分散λですから,Cλ2=1になります。
サービス時間分布は、指数分布(M) と一定(D) との間になります。
・M/M/1のとき:補正係数=1
・M/D/1のとき:Cμ2=0 → 補正係数=(1+0)/2=1/2
ですから、M/G/1の補正係数は1/2~1になります。
そのため、どのような分布になるよう制御しても、平均待ち時間は、M/M/1のときの1/2~1倍の間になる(1/2以下にはできない)といえます。