待ち時間の尺度
サービス時間が長いならば,ある程度長く待つのは仕方がないと感じますが,3分間の診療のために3時間も待たされるのでは不満が高まります。
どれだけ長く待つかの尺度として,μtが2以上になる確率はいくつかというように,μtを単位とすると便利です。μt=2ならば,t=2/μですが,1/μは平均サービス時間ですから,この場合は平均サービス時間の2倍より長く待つ時間はどれだけかということになります。
また,到着してからサービスを受けるまでの平均待ち時間はWqも,平均サービス時間との比率で表現すれば,μWqになります。
なお,リトルの公式により,行列に制限がないときは,
Wq=Lq/λ, Lq=L-λ/μ
ですし,窓口数をsとすれば,ρ=λ/sμなので,
μWq=L/sρ-1
でもあります。
なお,M/M/1のときはs=1,L=ρ/(1-ρ) ですから,
μWq=L/sρ-1=L
となります。
待ち時間がtよりも長い確率
客は,平均的な待ち時間よりも,長く待たされることが苦痛になります。M/M/1のときに,待ち時間がtよりも長い確率P>tは次の式で表されます。
P>t=ρ・e-(1-ρ)μt
これをグラフにすると,次のようになります。
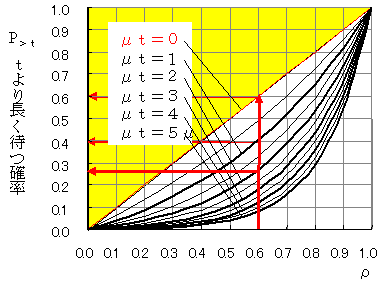
ρ=0.6のときを考えます。μt=0では0.6.μt=1では0.4,μt=2では0.27になっています。
μt=0というのは,待っている時間が0以上,すなわち待つ確率です。これが0.6になるのは明白でしょう。
μt=1とは,t=1/μですから,平均サービス時間よりも長く待つ確率です。すなわち,平均サービス時間よりも長く待つ確率が0.4だというのです。同様にμt=2では,待ち時間が平均サービス時間の2倍以上である確率が0.25であることを示しています。
M/M/sでの待ち時間
例によって,窓口が複数になると,とたんに式が複雑になります。

となります。計算式はゴツイですが,ρとsを与えればPt>0は計算できますし,Pt>τもμtを単位にすれば計算できますので,数表あるいは図表ができています。
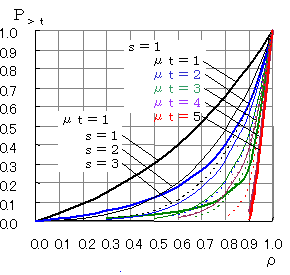
かなりゴチャゴチャとしたグラフですが,窓口の個数(s)が1のとき太線,2のとき細線,3のとき点線になっており,待ち時間μtが1のとき黒線,2のとき青線,3のとき緑線などとなっています。
たとえば,ρ(=λ/sμ)=0.6のとき,s=1でのμt=1では0.4,2では0.18,3では0.05となっています。すなわち到着してからサービスを受けるまでの時間が,平均サービス時間(1/μ)よりも長い確率が0.4,その2倍以上が0.18,3倍以上が0.05の確率であると読取れます。
次に窓口数での影響では,ρ=0.6のとき,平均サービス時間よりも長く待つ確率は,窓口が1つのとき0.4,2つのとき0.2,3つのとき0.11と読取れます。すなわち,同じρの値であっても,窓口数が増大することにより,サービスを待つ時間が短くなります。