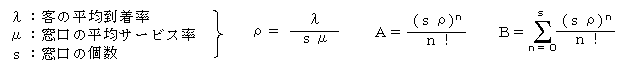
とすると,
P0:系の中の人数が0である確率
Pn≧s:窓口がすべてふさがっている確率
P>t :サービスまでの待ち時間がtより長い確率
μWq:サービスまでの平均待ち時間(単位:平均待ち時間)
は,次のようになります。

スタートページ> Web教材一覧> オペレーションズリサーチ> 待ち行列
参照:M/M/s(∞)とM/M/s(s)の「公式」と 「計算プログラム」
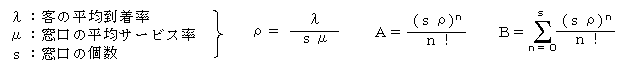

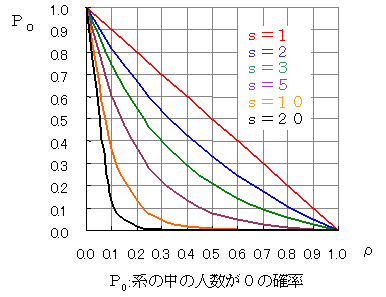
窓口の個数s=2,平均到着率λ=12,窓口1つの平均サービス率μ=10であるとき,ρ=λ/sμ=0.6ですから,窓口が2つとも空いている確率P0=2.5,窓口が2つともサービス中であり,待たなくてはならない確率P≧s=0.45が得られます。
また,s=2,λ=12のとき,待たせる確率P≧sを0.2にするためには,ρ=0.37ですが,ρ=λ/sμからμ=λ/sρ=12/(2×0.37)=16.2にする必要があることがわかります。
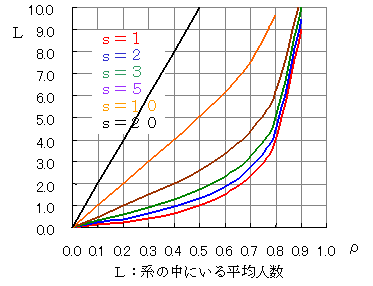
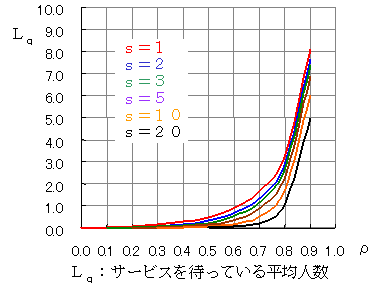
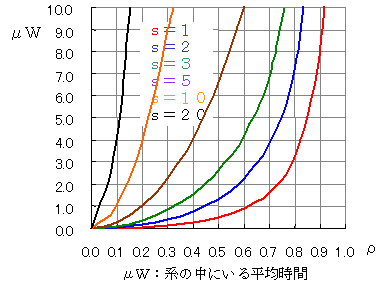
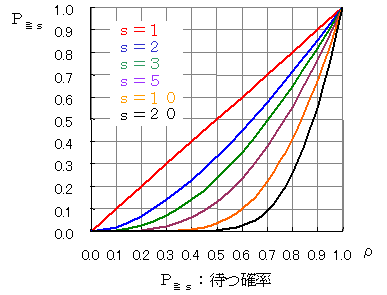
縦軸がμWになっていることに注意してください。たとえば,s=2(青い線)で,λ=12,μ=10のとすると,ρ=λ/sμ=0.6で,μWは2.3となります。これは,W=2.3/μ2.3/10=0.23であることを示します。すなわち,縦軸は平均サービス時間の倍数なのです。
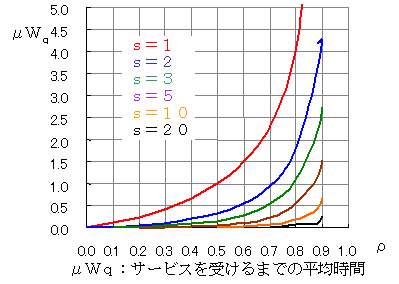
μWqのグラフの縦軸が1.0は,到着してからサービスを受けるまでの平均待ち時間が,平均サービス時間と等しい,すなわち,1人分のサービス時間を待つことになります。そのときのs=2のρは0.7ですので,μ=12/(2×0.7)=8.5になります。
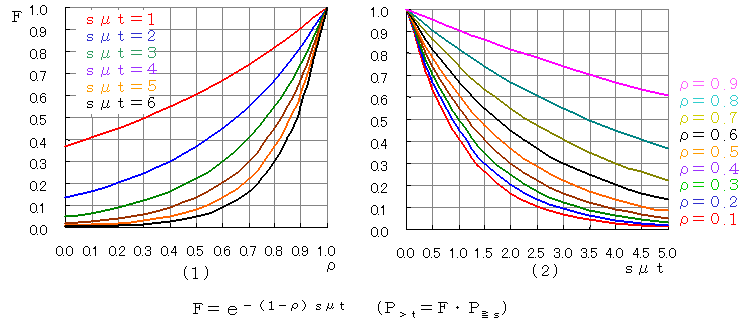
P≧t=P≧s・e-(1-ρ)sμtですが,上のグラフは,F=e-(1-ρ)sμtを示しています。(1)は,ρを横軸にして,sμtをパラメタにしたものであり,(2)は横軸にsμtをとって,ρをパラメタにしています。
s=2,λ=12,μ=10のとき,待ち時間が2/μ=0.2以上になる確率,すなわち,平均サービス時間の2倍以上待たされる確率を求めましょう。
ρ=λ/sμ=0.6ですから,P≧sのグラフからP≧s=0.45です。また,s・μt=2×2=4ですから,(1)のグラフからF=0.2となり,
P≧t=P≧s・e-(1-ρ)sμt=0.45×0.2=0.09
が得られます。また,(2)のグラフでも,sμt=4,ρ=0.6からF=0.2となり,(1)の結果と同じになります。
この場合は,「待ち」は生じませんので,
P0:系の中の人数が0の確率(窓口全体が空いている確率)
PS:すべての窓口がふさがっている確率(サービスが受けられない確率)
だけを示します。
また,この場合はρ≧1でも意味がありますので,ρ=0~1のグラフとρ=0~10のグラフを示します。
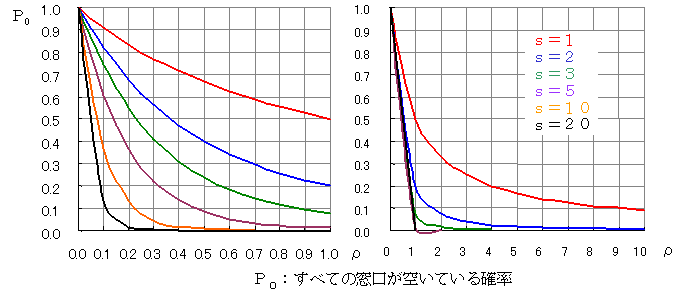
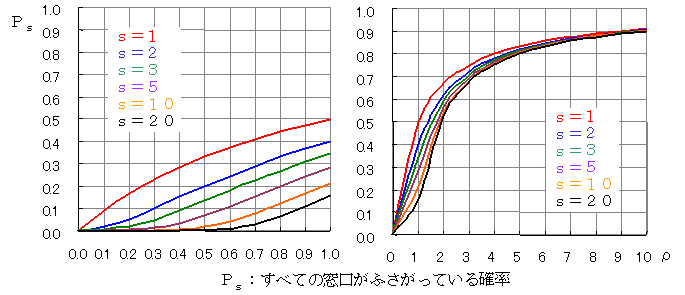
s=2,λ=12,μ=10(ρ=0.6)のときは,PS=0.24となります。
逆に,λ=12のときに,s=2とするならば,μをどの程度にすればよいかを考えましょう。PS=0.2,s=2からρ=0.5となります。ρ=λ/sμですから,μ=λ/sρ=12/(2×0.5)=12が得られます。同様に,s=3ならば,ρ=0.62となり,μ=12/(3×0.62)=6.5となり,s=2のときの約半分の能力でよいことがわかります。