待ち行列の基本形（Ｍ／Ｍ／１）

参照：JavaScriptの計算プログラム

Ｍ／Ｍ／１モデル

待ち行列のうちで最も基本的なモデルであるＭ／Ｍ／１（厳密にはＭ／Ｍ／１(∞)といいます）。　このＭはマルコフ過程（Markov Process）の意味で、「未来の挙動が現在の値だけで決定され、過去の挙動と無関係な確率過程」であるということです。
　すなわち，客の到着間隔や窓口のサービス時間は、それまでの客の到着が増加傾向にあるとかレジ時間の長いことにクレームがあるので、次の顧客到着間隔は小さくなるとかサービス時間を短くしようなどの変化はないという仮定です。

Ｍ／Ｍ／１モデルとは、
　　　客の到着および窓口のサービスの分布がランダム
　　　窓口の個数が１個
　　　客が到着したときに先客がいれば，自分の番になるまで待つ
の場合を検討します。
　ここでの考え方は，他の場合での基本になるものですから，十分に理解することが必要です。

公式を求めるプロセス

客が単位時間に到着する平均値（平均到着率）をλ（ラムダと読む）［人／時］，１つの窓口が単位時間にサービスを完了する人数の平均値（平均サービス率）をμ（ミューと読む）［人／時］とします。

系の中にｎ人がいる確率

サービスを受けている人とサービスを待っている人の全体（これを「系の中」という）の人数がｎ人である確率をＰ_nとします。

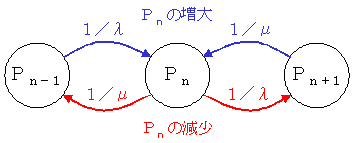
系の状態が安定しているということは，ある時刻ｔでのＰ_nと，ｔ＋⊿ｔでのＰ_nが等しいということですから，
　　　　ｔでｎ－１人だったのが，ｔ＋⊿ｔでｎ人になる　　　λ⊿ｔＰ_n-1
　　＋　ｔでｎ－１人だったのが，ｔ＋⊿ｔでｎ人になる　　　μ⊿ｔＰ_n+1
　　＝　ｔでｎ人だったのが，ｔ＋⊿ｔでｎ＋１人になる　　　λ⊿ｔＰ_n
　　　　ｔでｎ人だったのが，ｔ＋⊿ｔでｎ－１人になる　　　μ⊿ｔＰ_n
が成立する必要があります。すなわち，λＰ_n-1＋μＰ_n+1＝（λ＋μ）Ｐ_n　が成立します。
　しかし，上の式はｎ＝０のときには，Ｐ_n-1がＰ_－１になってしまいます。Ｐ₀とＰ₁の間では，⊿ｔの間に，
　　　　ｔで０人だったのが，ｔ＋⊿ｔで１人になる　　　λ⊿ｔＰ₀
　　＝　ｔで１人だったのが，ｔ＋⊿ｔで０人になる　　　μ⊿ｔＰ₁
すなわち，　λＰ₀＝μＰ₁　となります。

この状態方程式，
　　　λＰ_n-1＋μＰ_n+1＝（λ＋μ）Ｐ_n
　　　λＰ₀＝μＰ₁
を，ρ＝λ／μとおいて解くと，
　　　Ｐ_n＝ρ^ｎＰ₀
となります。
　ところで，　Ｐ₀＋Ｐ₁＋Ｐ₂＋・・・＋Ｐ_n＋・・・＝１ですから，
　　　（１＋ρ＋ρ^２＋・・・＋ρ^ｎ＋・・・）Ｐ₀＝１
となり，
　　　系の中の人数が０人である確率　　Ｐ₀＝１－ρ
　　　系の中の人数がｎ人である確率　　Ｐ_n＝ρⁿ(１－ρ)
が得られます。（その証明）

　　　　　Ａ＝１＋ρ＋ρ^２＋・・・＋ρ^ｎ
　　　　ρＡ＝　　ρ＋ρ^２＋・・・　　　＋ρ^ｎ+1
（１－ρ）Ａ＝１－ρ^ｎ+1
　　　　　Ａ＝(１－ρ^ｎ+1)／(１－ρ)
ここで，０＜ρ＜１　ですから，ｎ→∞のときはρ^ｎ+1→０になります。
従って，　Ａ＝１／(１－ρ)　が得られます。

人数と時間の平均値

系の中にいる人数（サービス中の人数も含む）の平均値Ｌは，
　　　Ｌ＝１Ｐ₁＋２Ｐ₂＋・・・＋ｎＰ_n＋・・・
　　　　＝（１ρ＋２ρ²＋・・・＋ｎρⁿ＋・・・）（１－ρ）
　　　　＝ρ／(１－ρ)
となります。（その証明）

　　　　Ｂ＝１ρ＋２ρ²＋・・・＋ｎρⁿ
　　　ρＢ＝　　　１ρ²＋・・・＋(ｎ－１)ρⁿ＋ｎρⁿ⁺¹
(１－ρ)Ｂ＝｛１ρ＋１ρ²＋・・・＋１ρⁿ｝－ｎρⁿ⁺¹
ｎ→∞のときｎρⁿ⁺¹→０であり，｛　｝の中はρＡ＝ρ／(１－ρ) なので
Ｂ＝｛ρ／(１－ρ) ｝／(１－ρ)＝ρ／(１－ρ)²
したがって，　Ｌ＝Ｂ(１－ρ)＝ρ／(１－ρ)　が得られます。

到着してからサービスを受けるまで待っている（サービス中の人は含まない）の平均値Ｌ_qは，
　　　Ｌ_q＝１Ｐ₂＋２Ｐ₃＋・・・＋(ｎ－１)Ｐ_n＋・・・
　　　　＝（１ρ²＋２ρ³＋・・・＋(ｎ－１)ρⁿ＋・・・）（１－ρ）
　　　　＝Ｌρ＝ρ^２／(１－ρ)
となります。

到着してからサービスを受けるまでの平均待ち時間Ｗ_qは，待っている人数Ｌ_qにより生じたのですし，平均到着間隔は１／λですから，全体ではＬ_q／λの時間がかかったことになります。すなわち，
　　　Ｗ_q＝Ｌ_q／λ
となります。
　　　　系の中にいる全時間Ｗは，待っている時間とサービス時間の合計なので，
　　　Ｗ＝Ｗ_q＋１／μ＝（Ｌ－λ／μ）／λ＋１／μ
　　　　＝Ｌ／λ
になります（Ｌ／μではないことに注意！）。

公式のまとめ（これは覚えてください）

　　客の平均到着率：　　　　λ［人/時］　⇔　平均到着間隔：　　１／λ［時/人］
　　窓口の平均サービス率：　μ［人/時］　⇔　平均サービス時間：１／μ［時/人］
　　　　ρ＝λ／μ　窓口の稼働率，客が到着したとき待ちが生じる確率

　　系の中に人がいない確率：　Ｐ₀＝１－ρ　（待たないでよい確率）
　　系の中にｎ人がいる確率：　Ｐ_n＝ρⁿＰ₀＝ρⁿ／(１－ρ)
　　
　　サービスを待っている人の平均人数：Ｌ_q＝ρ²／(１－ρ)
　　サービス中も含む系内の平均人数：　Ｌ＝Ｌ_q＋λ／μ＝ρ／(１－ρ)

　　到着してからサービスを受けるまでの平均待ち時間：　Ｗ_q＝Ｌ_q／λ＝λ／μ(μ－λ)
　　到着してからサービスを受けて去るまでの平均時間：　Ｗ＝Ｗ_q＋１／μ＝１／(μ－λ)
　　　（上の赤い部分がリトルの公式です。）

なお，上式を変形すると，
　　　Ｌ ＝ρ／(１－ρ) 　　Ｗ ＝Ｌ／λ
　　　Ｌ_q＝Ｌρ　　　　　　 Ｗ_q＝Ｗρ
となります。Ｌ_qやＷ_qは，ＬρやＷρに似ていますね！？

Ｌ，Ｌ_qのグラフ

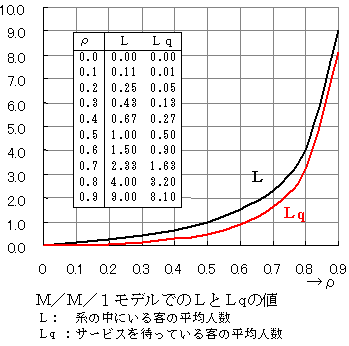
下図は，ρとＬ，Ｌ_qの関係をグラフにしたものです。
　これから，ＬやＬ_qはρが１に近づくにつれて急激に増大することがわかります。客の到着間隔が１０分，サービス時間が９分であるとき，これらが一定であれば待ちは生じないのに，それらがランダムなために，サービスを待っている人数が８人，サービスを受けている人も入れると９人になるのです。このようなことは直感とかなり異なりますね。このようなことを計画時に知っていないと，実施時に大きなトラブルになります。

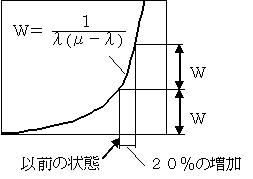
有名な例を紹介しましょう（大前義次，森村英典『待ち行列の理論と実際』日科技連，1962. p.46より）。第２次世界大戦中，アメリカからイギリスへの護送船団は，ニューヨーク港から８０％，バルチモア港から２０％から出港していた。米海軍は，それを不経済だと考え，すべてニューヨーク港から出港することにした。ところが，出港のための所要時間が従来の２倍になってしまった。米海軍は，敵国工作員によるサボタージュが行われたのではないかと調査をしたが，そのような事実はなく理由不明であり，ＯＲグループに原因解明を依頼した。その結果は・・・
　おわかりですね。ニューヨーク港での到着率の２０％の増加が，Ｗを急激に増大させていたのです。

例題

１台のレジがある。客の到着が１時間あたり平均１２人であり，レジでの所要時間は平均３分であるとき，次の値を求めよ。
　１　到着したとき，すぐにサービスが受けられる確率
　２　系の中にいる人の平均人数
　３　サービスを待っている人の平均人数
　４　到着してからサービスを受けて去るまでの平均時間
　５　到着してからサービスを受けるまでの平均待ち時間 ☆
客の到着が１時間あたり平均１２人→λ＝１２／６０＝１／５［人/時］
レジでの所要時間は平均３分→μ＝１／３［人/時］
　　ρ＝λ／μ＝（１/５）／（１/３）＝３／５＝０.６
１　Ｐ₀＝１－ρ＝１－０.６＝０.４
２　Ｌ＝ρ／(１－ρ)＝０.６／(１－０.６)＝１.５［人］
３　Ｌ_q＝Ｌρ＝１.５×０.６＝０.９［人］
４　Ｗ＝Ｌ／λ＝１.５×５＝７.５［分］
５　Ｗ_q＝Ｗρ＝７.５×０.６＝４.５［分］
上記の客の到着が２倍の平均２４人になった。到着してからサービスを受けて去るまでの平均時間を変えないためには，レジの平均サービス時間を何分にしなければならないか。 ☆
客の到着が２倍になったのだから，窓口のサービスも２倍にすればよいと考えて，３/２秒とするのは誤りです。
　Ｗ＝１／(μ－λ) ですから，客が増加したときの平均到着率をα，平均サービス率をβとすれば，
　　　１／(μ－λ) ＝１／(β－α)
　　　β＝μ－λ＋α
　　　　＝（１/３）－（１／５）＋（２４／６０）＝８/１５
　　∴　１／β＝１５/８≒１.９［分/人］

発展：行列長さや待ち時間の分布など

系中にいる人数

系中にn人がいる確率 p(n)は、前述のように、
    p(0) ＝１－ρ
　　p(n) ＝ρⁿ(１－ρ)
になります。

系中の人数がn人以下の確率Ｐ(≦n)は、次式で求められます、
　　Ｐ(≦n) = p(0) + p(1) + … + p(n)
            = (１－ρ) + ρ¹(１－ρ) + ρ²(１－ρ) +  … + ρⁿ(１－ρ)
            = 1 - ρⁿ⁺¹

「確率Ｐで、系中の人数はn人以下である」を求めるには、
    Ｐ(≦n) = 1 - ρⁿ⁺¹ を変形して、
    n = log(1-Ｐ)/log(ρ) - 1
  になります。
　しかし、 Ｐ(=0) ＝１－ρ ですから、Ｐ≦１－ρ　のときは、ｎ＝０になります。

待ち行列の長さ

系中の人数 nq と n=次の関係があります。
待ち行列の長さ nq は系中の人数 n からサービス中の人を除いた数になります。
待ち行列の長さが nq の確率 pq(nq) は、系中の人数 n の確率 p(n) を用いると pq(nq) = p(n-1) になります。
しかし、n=0, 1 のときは考慮する必要があります。
　　n　nq　     pq(nq)
　　0　 0       
    1   0    (1-ρ)+ρ(1-ρ)
    2   1    ρ²(1-ρ)
    3   2    ρ³(1-ρ)
    n  nq-1  ρ^nq(1-ρ)
   n+1  nq   ρ^nq+1(1-ρ)

待っている人の数（待ち行列長さ）が nq 人である確率　pq
    pq(0)  = p(0)+p(1) = 1-ρ²
    pq(nq) = ρ^nq+1(1-ρ)

待ち行列長さが nq 人以下である確率 pq
    pq(0) = pq(0) = 1-ρ²
    pq(nq) = pq(0) + {pq(1) + pq(2) + … + pq(nq)}
       = 1-ρ² + (1-ρ){ρ² + … + ρ^nq+1}
       = 1-ρ^nq+2

「確率Ｐqで、待ち行列長さが n 人以下である」
    Ｐq = 1-ρ^nq+2 から、n = log(1-Ｐq)/log(ρ) - 2    (Ｐq≦１－ρ　なら　n=0）

待ち時間

到着してからサービスを受けるまでの時間がｔ以上である確率
    待ち行列の長さから計算することもできるでしょうが、次の式があります。
    Ｐq(≧t) = ρｅ^-(1-ρ)μt

上側確率 Ｐ での待ち時間 t を求めるには、上式から次式がえられます。
    t = log(ρ/Ｐ)/(1-ρ)μ

到着してからサービスを受けるまでの時間がｔである密度関数
    Ｐq(≧t)は累積確率ですので、これを t で微分すれば密度関数になりますが
　　上側からの累積ですので t → t-dx での微分になり、符号を反転する必要があります。
        p(t) = ρ/(1-ρ)μ * ｅ^-(1-ρ)μt
    
系中での全時間
    待ち時間にサービス時間 1/μ を加えたものが全時間ですから、
    Ｐ(≧t) = Ｐq(≧t) + 1/μ
            = ρｅ^-(1-ρ)μt + 1/μ