分散分析とは
分散分析とは、各因子に複数の水準(グループ)があるとき、因子の水準により平均に差があるかどうかを検定する分析方法です。
例えば作業者A,B,Cが機械P,Qを使用して製品を生産しているとします。このとき、作業者、機械を因子といい、作業者A,B,Cを作業者の水準、機械P,Qを機械の水準といいます。因子数は2で、作業者因子は3水準、機械因子は2水準です。
分散分析とは、A-P、A-Q、・・・、B-Pなどの因子の組み合わせについて、いくつかの標本を採取し、作業者や機械により製品の品質に差があるか(平均に有意差があるか)どうかを検定する方法です。
因子数が1のときを一元配置分散分析、因子数が2のときを二元配置分散分析といいます(3以上のときを多元配置分散分析といいますが、複雑ですので省略します)。
二元配置分散分析は、因子数が2のとき、例えば、品質に影響する因子として、作業者と機械が考えられるようなときに用いられます。この場合、ある特定の作業者と機械の組み合わせのときに品質がよいということが考えられます。このように、因子間での効果を交互作用といいます。
二元配置分散分析のとき、各因子の水準について、1つのデータしかない場合(「繰返しがない」という)と、複数組のデータがある場合(「繰返しがある」という)があります。前者の場合は、1つのデータだけでは、交互作用を考えることができません。後者では交互作用が重要になります。
一元配置分散分析
一元配置分散分析では、因子が1つの場合です。ここでは、作業者A,B,Cの3人(3水準)により品質に差があるか(平均に有意差があるか)どうかを検定することにします。
水準数が2のとき、すなわち作業者がAとBの2名のときは、2つの母集団の平均の差の検定ですから、t検定が利用できます(参照:「t分布と推定・検定」)。
ところが、水準数が3以上になると、t検定では、2つずつの検定はできても、全体についての検定はできません。
検定では、帰無仮説を立てて、それが棄却されるかどうかを判定します。分散分析では、次のようになります。
- 帰無仮説 H0:A-B、B-C、C-Aの3の組み合わせのすべてについて、平均に差があるとはいえない(積極的に差がないというのではなく、「有意水準で差がある」とはいえないという意味)。
- 対立仮説 H1:上の組み合わせうち、少なくとも1つは差がある(すべての組み合わせで差があるといっているのではない)。
考え方のイメージ
分散分析で水準Aも全体の分布も、その母集団は正規分布をしていると仮定します。
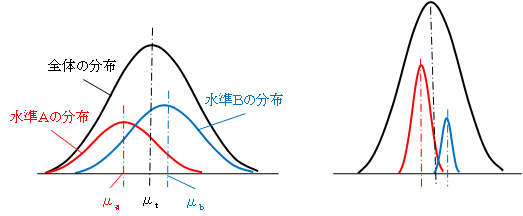
下左図のように、水準Aの平均μaが、全体の平均μtと離れていても、ばらつきが大きいときには、差があるとは断定できません。逆に、下右図のように、平均の差が小さいようにみえても、ばらつきがほとんどないときには、差があるといえます。
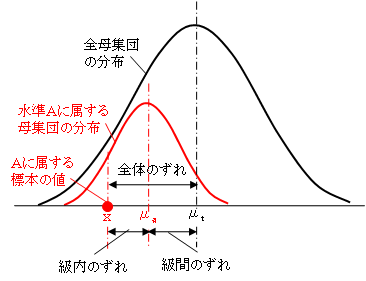
水準Aに属する標本について、その値と全体平均μtのずれは、水準Aの平均μaがμtからずれていること(図では「級間のずれ」と表記)と、標本値がμaからずれていること(図では「級間のずれ」と表記)2つに分解することができます。
級間のずれが大で級内のずれが小さいとき、水準の平均の間に差があるといえます。
統計学的な接近
ばらつきやずれの尺度に平方和や分散があります。平方和Sは、
S=Σ(標本の値-平均)2
となります。
全体の平方和は、
全体の平方和=St=Σ(全標本-全体の平均μt)2
となります。そして、水準Aの平方和として、
水準Aの平方和=Sa=水準Aの標本数×(水準A平均μa-μt)2
と定義します。同様に、
水準Aの平方和=Sa=水準Aの標本数×(水準A平均μa-μt)2
水準Aの平方和=Sa=水準Aの標本数×(水準A平均μa-μt)2
とし、その合計を
S*=Sa+Sa+Sa
とします。また、
となります。そして、
St-S*=Se=残差平方和
と定義します。
平方和は標本の個数に関係しますので、平方和/自由度により調整します。全体の自由度φtは、全標本数をnとすれば、φt=n-1です。S*の自由度は、水準数をmとすると、φ*=m-1になります。そして、残差Seの自由度φeは、φe=φt-φ*=n-mになります。
st2=St/(n-1) ・・・ 全変動といいます
s*2=S*/(m-1) ・・・ 級間分散といいます
se2=Se/(n-m) ・・・ 級内分散といいます
すると、
(n-1)×全変動=(m-1)×級間分散+(n-m)×級内分散
の式が成立します。
ここで、各水準平均と全体平均の差が大きいと級間分散が大になり、級内分散が大きいことは、この因子以外の影響によるばらつきが大きく平均に差があっても有意差とはいえないことを考えると、検定の尺度として、
分散比=級間分散/級内分散
を用いるのが適切であることがわかります。
分散比の検定では、F検定が用いられます。すなわち、上記の計算で求めた分散比Fが、有意水準5%の自由度(n-1、n-m)のF0.05より大であれば、帰無仮説 H0が棄却された(水準間で有意差がある)ことになります(参照:「F分布と推定・検定」)。
なお、F分布はχ2分布の比で表されます。自由度(p,q)のF分布は、
F=(χ2p/p)/(χ2q/q)
となります。それで、p=1のとき、すなわち、因子の水準数mが2のときは、F検定ではなく、χ2検定が用いられます。(参照:「χ2分布と推定・検定」)
数値例
作業者A,B,Cの3人による製品の品質について、次の標本(観測データ)が得られました。
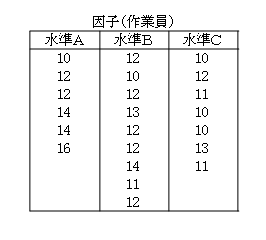
上述の「統計学的な接近」で示した手順で計算すると、次の結果が得られます。
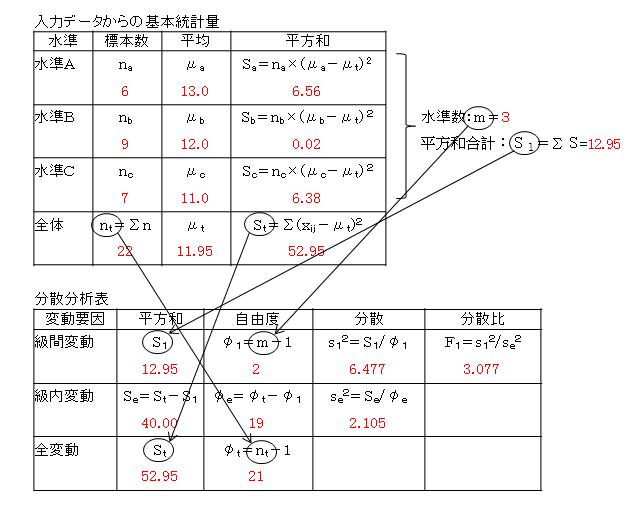
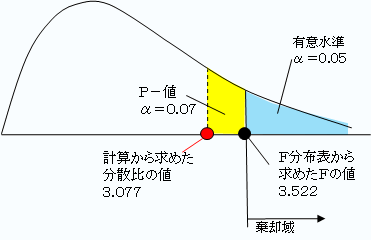
結果として、分散比=3.077となります。
F分布表から、自由度(2、19)で上側確率0.05の値をみると、F=3.522です。
計算による分散比<表によるFの値
なので、帰無仮説 H0が棄却できない、すなわち「A-B、B-C、C-Aの3の組み合わせのすべてについて、平均に差があるとはいえない」ことになります。
Excelによる計算
Excelには、分散分析のためのツールがあります。上記の入力データによる結果は次のようになります。

Excelでの用語は、本文での用語と異なるものがあります。「級」を「グループ」、「平方和」を「変動」、「分散比」を「観測された分散比」と表現しています。
「F境界値」とは、F分布表から求めたFの値のことです。「P-値」とは、「観測された分散比=F境界値」となる有意水準です。すなわち、この結果では、「観測された分散比=3.077<3.522=F境界値」なので、有意水準0.05では棄却できないが、有意水準が0.070(P-値)ならば棄却できることを示しています。
この数値例では、観測された分散比とF境界値の差はわずかであり、5%では棄却できないが7%で棄却できる、すなわち、95%の信頼度で差があるとはいえないが、93%の信頼度なら差があるといえることを示しているのです。
繰返しのない二元配置分散分析
二元配置分散分析の特別なケースとして、各水準の組み合わせの標本が1つしかないとき、「繰返しのない」二元配置分散分析といいます。実際に1つのデータしか得られない場合や、平均値しかわからない場合に用いられます。
この場合は、標本が1つだけなので、分散を計算することができません。それで、交互作用はないとして計算します。一元配置と同様に、全分散を級間変動1、級間変動2、級内変動とに分け、級間変動1/級内変動、級間変動2/級内変動を求めればよいのです。
数値例
因子1を機械(P,Q)、因子2を作業者(A,B,C)として、入力データと計算結果、Excelによる結果を示します。
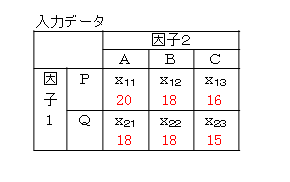
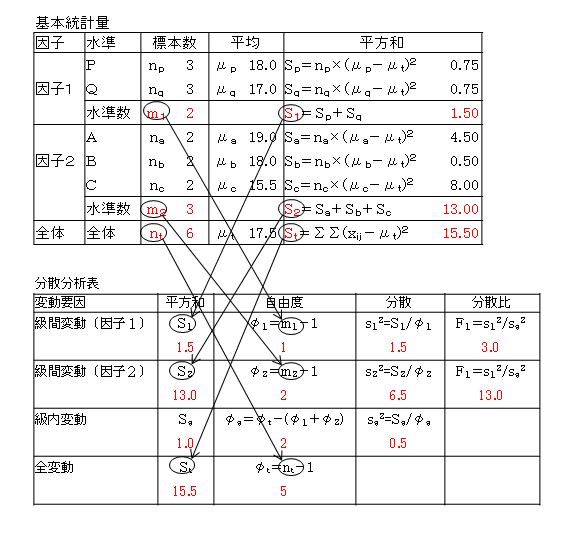
Excelによる結果

因子1(機械)では、P-値=0.225という大きな値になっています。すなわち、信頼度を80%程度に下げても帰無仮説が棄却されないのですから、この場合は「機械による差はない」といってもよいでしょう。このことは、「基本統計量」に時点で、機械の平均差が1.0、平方和が1.50であり、他の値と比較して小さいことからも想像されます。
繰返しのある二元配置分散分析
機械Pと作業者A、機械Bと作業者Cなど各水準の組合せについて複数のデータがある場合は、交互作用を考えなければならないので、複雑になります。また、ここでは、そのテータ個数がすべて同じ(数値例では5)とします。異なる場合は、さらに複雑になります。
機械Pと作業者Aの組合せの場合、その標本数をnpa、その平均μpaと全体平均μtとの平方和をSpaとすると、
Spa=npa×(μpa-μt)2
となります。
これを、すべての組合せについて行い、それを合計した値を、
S*=Spa+Spb+・・・+Sqc
とします。
これまでの類推から、St-S*は、残差の平方和Seになります。すなわち、S*は、各因子の級間の平方和と交互作用の平方和の合計になります。それで、
交互作用の平方和S1・2=S*-(因子1の平方和S1-因子2の平方和S2)
になります。
そして、交互作用の自由度φ1・2は、因子1の自由度φ1と因子2の自由度φ2の積になります(この説明は難解のため省略)。すなわち、
φ1・2=φ1×φ2=(m1-1)×(m2-1)
となります。
これ以外は、繰返しのない二元配置分散分析と同様の手順で計算できます。
数値例
各水準の組合せでの標本数を5とします。組合せの数は6なので、全体ではnt=6×5=30、因子1水準Pでは、因子2の水準数が3なので、np=3×5=15、因子2水準Aでは、因子1の水準数が2なので、na=2×5=10などとなります。
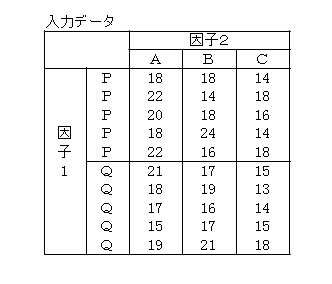
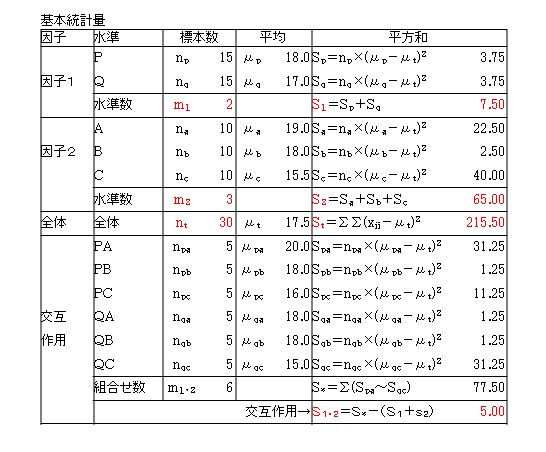
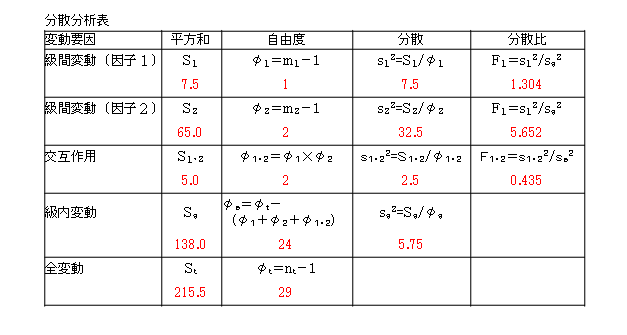
Excelによる結果
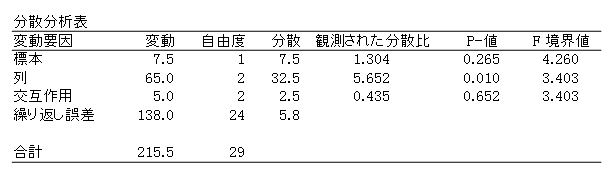
列(因子2=作業者)では、分散比=5.652>3.403になり、帰無仮説が棄却され「有意差がある」ことになりました。しかも、P-1の値が0.010になので、0.01確率すなわち99%の信頼度で有意差があることになります。
実は、「繰返しのない二元配置分散分析」の入力データは、本ケースでの平均を与えたのです。このように平均では同じであっても、複数データのときは、水準の組合せによるばらつきにより、交互作用が認められることがあり、それを考慮すると、有意差が明確になることがあるのです。
なお、交互作用の影響をどのように分析するかに関しては、さらに高度な分析方法があります。すべての水準で得られるデータ数が異なる場合を考慮すると、どのような水準を設定して、どのデータを得ればよいかなどの問題に発展します。そのような分野に実験計画法などがあります。