最小二乗法では回帰を用いました。変数間の関係では相関を用いました。対応する変量xとyの間の関係度合を表す尺度に回帰と相関があります。では、回帰と相関とは、どこが違うのでしょうか?
違いのイメージ
xとyの変数があります。回帰ではxを説明変数、yを被説明変数といいます。説明変数が1つの回帰を単回帰、変数が2つの相関を単相関といい、説明変数が複数のときを重回帰、変数が3つ以上のときを重相関といいます。重回帰や重相関に場合は複雑になるので、別章にまわし、ここでは単回帰と単相関について取り扱います。
回帰とは、xが決まればyが決まるという関係(x→y)で、それに対して、相関とは、xとyが同等の関係(x-y)だという違いです。
例えば、xを身長、yを体重としたとき、身長から体重を推定できないかと考える(体重から身長を推定することは考えない)のが回帰であり、方向性を考えずに、身長と体重の間に関係があつかどうかを調べるのが相関です。
回帰では、点(x,y)とそのxにおける直線上の点(x,y*)の距離をyの高さの差、すなわち、ε=y-y* を誤差εとし、ε2を最小にする直線(y=a+bx)を求めます(参照:「最小二乗法」)。
そして、直線の傾きbのことを、(変数xのyに対する)回帰係数といいます。
それに対して、回帰では、方向性を考えずに、xとyの関係度合を示す尺度として、相関係数を考えます。この相関係数の絶対値が1に近いならば、xとyの関係が強い(やや厳密性を欠きますが、xとyが直線上に近接している)ことを示し、0に近いならば、xとyの間の関係が少ない(直線と離れている)ことを示しています(参照:「相関係数」)。
このように、回帰と相関は異なる概念なので、用途により使い分けることが必要です。しかし、直線の式(回帰式)を求める前に、まず相関を行って、関係があることを確認してから、あるいは複数の説明変数がある場合には適切な変数を選択してから、回帰により式を決定するのが一般的です。
単回帰と単相関
次のように、n(=10)組のxとyがあるとします。
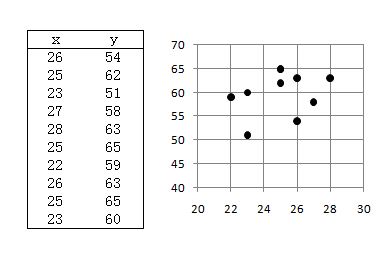
自由度:標本数n=10なので、φ=n-1=9
平均:μx=Σxi=(26+25+・・・+23)/10=25、μy=60
平方和:Sxx=Σ(xi-μx)2=(26-25)2+(25-25)2+・・・+(23-25)2=32.0、Syy=194.0
分散:sxx2=Sxx/φ=32.0/9=3.556、sxx2=21.56
標準偏差:sx=√sx2=√3.556=1.886、sy=4.643
積和:Sxy=Σ(xi-μx)(yi-μy)=(26-25)(54-60)+(25-25)(62-60)+・・・+(23-25)(60-60)=23.0
共分散:sxy2=Sxy/φ=23.0/9=2.556
参照:「平均、分散、標準偏差」、
「相関係数」
単回帰での回帰係数
説明変数xと被説明変数yを、直線
y=a+bx
で近似したとします。このbが(xのyに対する)回帰係数です。
このとき、各点(xi,xi)と直線との誤差をεiとすれば、
yi=a+bxi+εi
となります。
ここで、yの平均をμy、xの平均をμxとして、直線が点x,μy)を通るとすれば、Yi=yi-μy、Xi=xi-μxとすることにより、直線の式は、
Yi=b×Xi+εi+(a+bμx-μy
となります。右辺の( )は0ですから、
Yi=b×Xi+εi
となります。
回帰で、直線近似をするということは、
ε2=Σ(bXi-Yi)2
を最小にすることですから、ε2をbで偏微分して0とすればよく、
∂ε2/∂b=2ΣXi×(bXi-Yi)=0
∴ b=ΣXiYi/ΣXi2
となります。
ここで、ΣXiYi=Sxy、ΣXi2=Sxxですから、
b=Sxy/Sxx=23.0/32.0=0.718
となります。
また、sxy2=Sxy/φ、sxx2=Sxx/φ ですから、
b=sxy2/sxx2=2.56/3.56=0.718
から求めることもできます。
なお、yを説明変数、xを被説明変数にしたときの回帰係数は、
by→x=Sxy/Syy=23.0/194.0=0.119
となり、全く異なる直線になります。このことからも回帰では、方向性が重要であることがわかります。
単相関での相関係数
相関係数rは、次の式で定義されます。
r=Sxy/√Sxx√Syy=23.0/(√32.0×√194.0)=0.292
相関係数と回帰係数の間には、
bx→yby→x=(Sxy/Sxx)(Sxy/Syy)
=Sxy2/(SxxSyy)=r2
の関係があります。これからも、相関係数は方向性をもたない場合の変数間の関係を示す尺度だと理解できましょう。
単相関での寄与率、決定係数
y=a+bxによるyの計算値をy*とすると、
y-μy=(y-y*)+(y*-μy)
と変形できます。ここで、(y-y*)は回帰による偏差で、(y*-μy)は残差であり、この2つの間の相関係数は0ですから、上式の両辺の平方和は等しくなります。
Σ(y-μy)2=Σ(y-y*)2 + Σ(y*-μy)2
(全変動) (回帰による変動)(残差による変動)
ここで、y=a+bxがよく当てはまるということは、回帰による変動が大きく、残差による変動が小さいということです。それで、
回帰による変動 Σ(y-y*)2
r2=────────=───────
全変動 Σ(y-μy)2
のことを、寄与率あるいは決定係数といいます。
そして、単回帰、単相関のときは、
相関係数2=寄与率
であることが証明されています。それで、r2という記号を使うのです。
相関係数がどの程度ならよいかは、xとyの物理的意味により異なります。自然科学では高い相関が求められるでしょうし、社会科学ではあまり高い相関は期待できないでしょう。一般に、次のようにいわれています。
r r2 相関
±0.7以上 0.5以上 強い
±0.4以上 0.1以上 中程度
±0.2以上 0.05以上 弱い
±0.2以下 0.05以下 相関なし