相関係数 r は、(x1,y1),(x2,y2),・・・,(xn,yn)のように対応する2変数の間での、直線的な関係度合を表す尺度です。
下図は、散布図と相関係数の関係を示しています。ほとんど関係がない場合をr=0、右上がりの直線に一致するときをr=1、右下がりの直線になる場合を-1となります。

各点(xi,yi)と平均の点(x,y)との差を偏差といい、(xi-x)×(yi-y)を偏差積、その合計を偏差積和Sxyといいます。偏差積和から標本数nによる影響を除外するために、自由度φ(=n-1)で除したものを共分散sxy2といいます。
Sxyは1変数での平方和S、sxy2は1変数での分散s2(下図ではxのS、yのSなどを区別するために添字をつけています)に対応した概念です。

相関係数は2つの方法で求められますが、その結果は同じになります。
上左の式で相関係数を直感的に解釈します。ここで、分母は常に正です。そして、各点(xi,yi)と平均の点(x,y)との位置関係により、rの正負は次のようになります。
x-x y-y r
正 正 正
正 負 負
負 正 負
負 負 正
これから、散布図が右上がりならrは正、右下がりならrは負になります。
各点と平均の点が離れていれば、rの絶対値は大きくなるし、近ければ小さくなります。
分母で割ることにより、データの個数やデータの大きさの違い(単位の取り方など)の影響を取り去り、rの値を-1≦r≦1の間にする(正規化する)ことができます。
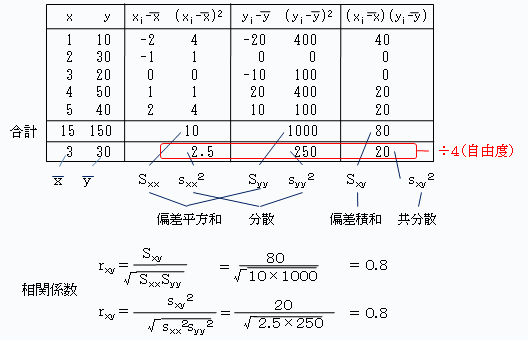
数値例