損得計算の考え方→線形計画法
「すべてこの世は金次第」とはいいませんが,経営での意思決定には損か得かの判断が重要な要素です。結論を先にいうと,損得計算では「比較の原則」と「制約条件の原則」が重要です。とかく損得を考えるときに会計的なアプローチをしがちですが,会計情報ではこの二つが明確ではありません。それをカバーする一つの考え方に線形計画法があります。
損得計算の基礎
Aケーキ店の問題
A社はケーキ店です。話を簡単にするためにケーキは1種類だけとします。毎日,早朝までに工場でほぼ100個のケーキを作り,店に陳列して販売するという見込生産体制になっているとします。
原価を計算したら,材料費や消耗品などケーキ生産個数に比例する費用(変動費)が70円/個であり,店舗費用や人件費など生産個数には無関係な費用(固定費)を生産個数で割ると50円/個になることがわかりました。それで,原価合計は,70+50=120円/個,売価は200円/個ですので,1個あたりの利益は200-120=80円になります。
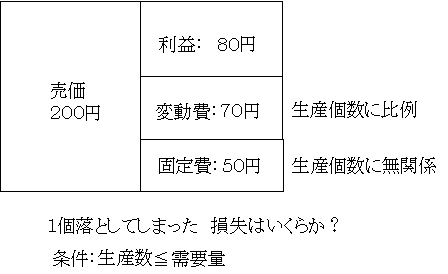
A社では,絶対に売り残しをしないことをポリシーにしており,生産量を需要量よりも少なくしていますので,いつも閉店以前に売り切れてしまいます。
ある日,店員が誤ってケーキを1個落としてしまい,廃棄してしまいました。それによる損失はいくらでしょうか? ただし,消費税や法人税などは考えないことにします。
いくつかの答があると思います。それをメモしておきましょう。
でも,「正解は一つ」であることはご了解いただけますね?
☆
損得計算では「精度」ではなく「正確」が重要!
おそらく「200円=売価」「80円=利益」「130円=売価-変動費」のように,複数の答があったと思います。どれか正解かはさておき,これから重要なことがいえます。
「損得を明確にしよう」というと,原価を精密に計算して「変動費は70円ではなく71.34円だ」とか,DPPやABMを適用して「間接コストも考慮したら75円になった」などとしがちです。よしんばその程度の違いがあったにせよ,200円と80円の違いから考えればたいしたことではありません。「販売個数が1個減少したのだから固定費配分が変わるはずだ」などもたいしたことにはなりません。
重要なのは「200円,130円,80円のどれが正しいのか」という考え方の「正確性」なのです。これを誤ったら,いかに原価計算の体系や計算処理を改善しても,損得計算はできないのです。
比較を明確に!
損得計算では比較の対象を明確にすることがコツです。ここでは「落とさなかったとき」と「落としたとき」で何が違うのかを考えればよいのです。
この違いは「落とさなかったときは,そのケーキを渡せば200円の代金が貰えたのに,落としたことによりそれが貰えなかった」ことだけです。原価がどうのこうのは全然関係がないのですね。「正解は200円の損」です。
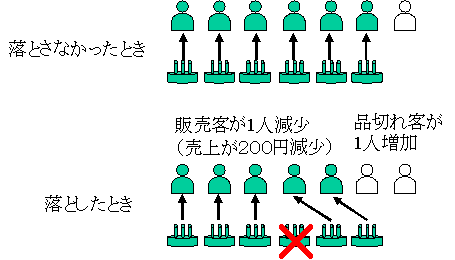
Bケーキ店の問題
Bケーキ店の売価や原価はAケーキ店と全く同じだとします。ただ異なるのは絶対に品切れを起こさないという方針であり,毎日閉店後には数個の売れ残りが生じて廃棄しています。
Bケーキ店で1個落としたらいくらの損失になるでしょうか? ☆
制約条件で価値が変わる!
1個落としても結果として「閉店後の売れ残り個数が1個減少した」だけですので,「正解は0円」です。
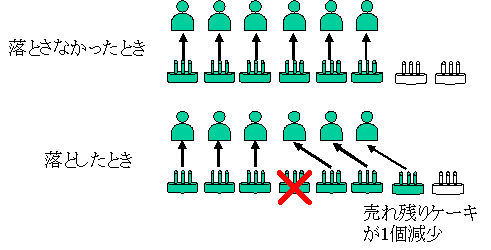
同じ「1個落とした」ことなのに,生産がネックだったAでは200円,そのネックがなく販売がネックであるBでは0円なのです。このように,損得計算では,制約条件により価値が変わることに留意してください。
このようなことは,単に会計業務をシステム化して検索加工システムを強化しただけでは解決できません。
そば屋の問題
ケーキ店は,いうなれば見込生産でした。それに対して,そば屋は客が注文を受けてから生産する受注生産です。売価や原価の構成はケーキ店と同じです。変動費は材料費と加工費になります。
そば屋に客が入ってきたのですが,何か用事を思い出したのか,注文をする前に出て行ってしまいました。出て行かなかったときと比較して,どれだけ損をしたでしょうか? (1)と(2)のそれぞれについて考えてください。
(1)Cそば屋は,閉店予定時刻前に材料がなくなるので閉店します。
(2)Dそば屋は,閉店時刻には材料は余っています。この材料は翌日にも使えます。☆

そば屋の解答
(1)普段は断っていた閉店直後の客にサービスすることができるだけなので,損は発生しません。「正解は0円」となります。
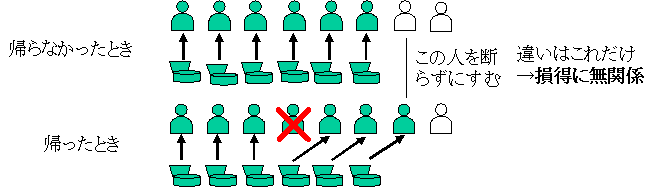
(2)「出て行った」ので売上も費用も発生しません。「出て行かなかった」ならば,変動費70円を支出することにより,200円の収入があるのですから,200-70=130円の利益が得られたはずです。「正解は130円」になります。
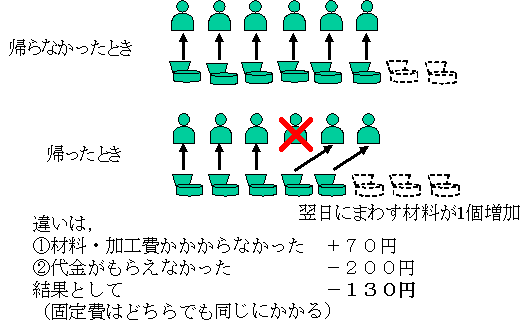
このように,CとA,DとBは一見同じように見えても,結果は全然違うのですね。このように「比較の原則」「制約条件の原則」をしっかり理解することが,損得計算をするのに重要なことなのです。
線形計画法
E製油所の問題
原料Aと原料B(原油?)を,装置Pと装置Qを通して,製品X(ガソリン?)と製品Y(重油?)を生産している装置産業を考えます。原料は,装置Pにより製品Xと製品Yに分離されますが,その得率が異なります。製品Yは装置Qを通すことにより製品Xにすることができます。原料や製品の価格,設備を通す費用,装置Pでの得率などは,下図に示してあります。
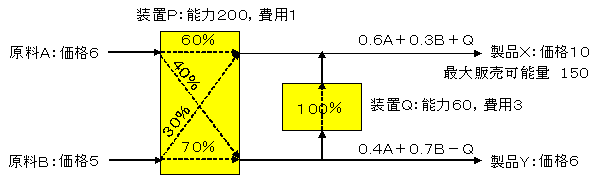
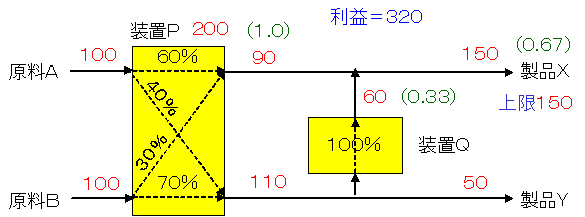
X≦150,P≦200,Q≦60の場合(これを「標準ケース」ということにします)について,利益(XとYの売上高-原料AとBの購入費用-装置PとQの費用)を最大にするX,Y,A,B,P,Qの値を求めてください。 ☆
線形計画法
おそらく,「Xは最大になる」や「Qも最大になるのでは?」というような仮定をして,穴埋計算あるいは連立方程式などを思い出して計算するのでしょうが,仮定が本当に正しいかどうか,どこかに矛盾が生じないか懸念が残ります。
この問題を数学的な式にしますと,次のようになります。
原料と装置の関係から: A+B≦P 中間製品と製品Xから: 0.6A+0.3B+Q≧X 中間製品と製品Yから: 0.4A+0.7B-Q≧Y 利益=10X+6Y-6A-5B-1P-3Q →最大
このあたりから拒否反応が出そうですが,これを解くのには線形計画法という方法があり,コンピュータで解くことができます。このような簡単なモデルならばExcelのソルバーで解くこともできます。実際の製油所モデルでは式の個数が数百から数千にもなりますが,線形計画法の専用ツールを用いれば簡単に解くことができ,石油業では日常的に使っています。
結果の最適解は図の赤字のようになります。緑色の( )はレジュースト・コストというもので,これが大変有効な概念であり線形計画法のウリなのですが,それについては後で・・・。
原価計算の危険
なぜ,AとBがこのような値になるのでしょうか?
Aを1使うことにより,Xが0.6,Yが0.4できるのですから,それによる収入増加は0.6×10+0.4×6=8.4円になり,Aの価格は6円,Pの費用は1円ですから費用増加は7円ですので,利益増加は8.4-7=1.4円になります。同様にBを1使うことにより,(0.3×10+0.7×6)-(5+1)=1.2の利益増加になります。Aのほうが0.2円有利ですからA=200としたくなります。
あるいは,Yの6円ではなく,Qを通すことによりXになるのだから10-3=7円を適用したらどうかという案もありましょう。それによればAは1.8円,Bは1.9円になり,こんどはB=200としがちです。
これが会計などで行われる原価計算ですね。これらのどちらも正しくないのです。それは,上記の制約条件を無視しているのが原因です。すなわち,損得計算に会計上の原価計算を使うのは危険なのです。それに対して線形計画法では,すべての制約条件を同時に満足する最適解が得られるというメリットがあるのです。
ここで問題です。製品Xは販売能力限界の150になりましたが,もし,Xの価格が9.2円ならばもっと売れるという情報が入りました。増産するべきでしょうか,断るべきでしょうか? ここで話を単純にするために,生産量は150→151にするだけだとし,安値販売による悪影響などはないこととします。 ☆
レジュースト・コストが損得計算の原価
単純にAが100%Xになるとすれば,AとPから原価は7円だといえます。Bも使うのであればそれよりも安くなります。また,Yを原料とするのだと考えればQの費用を加えて9円になります。どちらを採用するかで迷いますが,いずれにせよXの上限制約を1だけ緩めれば利益は1円以上増加すると考えられます。すなわち,9.2円ならば売れというのが,通常の会計的な限界利益の考え方からの結論です。
ところが実際にX≦150をX≦151に修正して線形計画法で解いた結果は下図のような変化になりました。赤色の数値は数量の増減,青色の数値は金額の増減です。利益は0.67円増加しました。利益増加=0とすれば,Xの増加分の価格は10-0.67=9.33円となります(このXのレジュースト・コストが0.67円という値は,このような再計算をしなくても,先の標準ケースで求められていたことを思い出してください)。すなわち,9.2円ならば断れというのが結論です。
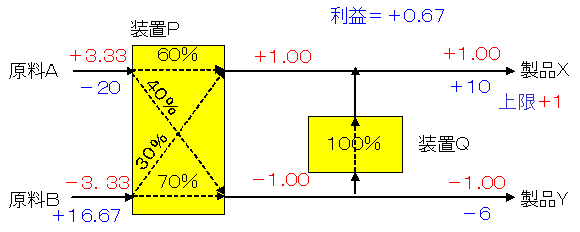
この違いは,会計的な限界利益では局所的な見方をしていたのに対して,線形計画法では「条件変化をしたときの最適な方法」と「以前の条件での最適な方法」を比較しているからなのです。線形計画法が「比較の原則」と「制約の原則」を満足する方法であることが,おわかりいただけたと思います。
決定するということ→決定理論,ゲームの理論
ここでの意思決定は,いくつかの選択肢があり,それを選択した後でいくつかの事態が発生する。選択と事態による結果の評価はできるが,どの事態が発生するのかわからないといったような問題を対象にします。
相手が自然のとき
利失表を作ろう
景気(好況・不況)と設備投資(積極案・消極案)の関係を例にします。積極案を選択した後で好況になれば,10(億円? 単位は適当に考えてください)の利益が期待できますが,もし不況になれば過剰投資になり-3の損失になります。また,消極案を選択したときは,好況でも5の利益しか期待できませんが,不況でも2の利益があると期待されるとします。
| ペイオフ・マトリクス | 景気 | ||
|---|---|---|---|
| 好況 | 不況 | ||
| 私の戦略 | 積極案 | 10 | -3 |
| 消極案 | 5 | 2 | |
積極案や消極案のように私が選択できる手段を私の戦略といい,好況や不況を相手の戦略といいます。そして,10や-3などの結果の利失の表を利失表(ペイオフ・マトリックス)といいます。相手の戦略がわからないのに,私は利益が最大になるようにいずれかの戦略を決定しなければなりません。
「オレが積極案を採用すれば景気はよくなるし,消極案をとれば不況になる」という楽観的な人ならば積極案をとるでしょうし,「どうせ物事はうまくいかないものだ」という悲観的な人は消極案を採用するでしょう。それは「信念」ですから,ここでの問題にしませんが,上のような利失表がはっきりしないと,自分の信念と異なる決定をしてしまうことになる危険もあります。
どのような決定をするのかの前に,利失表を作成することが必要なのです。数値化できればそれにこしたことはありませんが,どのようなことが起こるかを箇条書きに列挙するだけでも,問題を明確にするのに役立ちます。
| メリット・デメリット分析 | 決断の評価 | ||
|---|---|---|---|
| メリット | デメリット | ||
| 私の決断 | 投資をする | 生産が増える 新分野に進出できる |
過剰投資の危険 資金繰りの危険 |
| 投資をしない | 他への資源活用 財務の安定性 |
需要に応じられない 他社との競争に遅れる |
|
経営戦略での技法にSWOT分析がありますね。「己を知り敵を知れば百戦百勝」といいますが,自社の強みと弱み,環境の機会と脅威を下図のように整理することによって,進むべき方向を検討するのでした。利失表もSWOT分析によく似ています。
| SWOT分析 | 自社にとって | ||
|---|---|---|---|
| 有利 | 不利 | ||
| 環境 | 自社の能力 | 強み Strength | 弱み Weakness |
| 社外の環境 | 機会 Opportunity | 脅威 Threat | |
確率がわかっていれば・・・
もし,好況になることがわかっていれば,積極案を選択すれば10の利益があるのに,消極案だと5の利益にしかならないのですから,積極案を選択すればよいでしょう。不況だとわかっていれば消極案をとるでしょう。ところが,将来のことはわからないので,このような問題が存在するのです。
将来のことはわからないといいますが,主観的あるいはなんらかの調査により「6:4で好況だ」というような表現をすることがあります。これは,好況になる確率が0.6,不況になる確率が0.4だということですね。この確率がわかっていたら,どのような決定をしますか?☆
| 確率既知のとき | 景気 | 好況 | 不況 | 0.6 | 0.4 |
|---|---|---|---|
| 私の戦略 | 積極案 | 10 | -3 |
| 消極案 | 5 | 2 | |
期待値の考え方
おそらく次のような考え方をするでしょう。
積極案を選択すれば,10×0.6-3×0.4=4.8
消極案を選択すれば, 5×0.6+2×0.4=3.8
となるので,積極案のほうが有利であると判断するでしょう。
ここでの4.8や3.8のことを期待値といいます。すなわち,確率既知の場合には期待値が最大の戦略を選択することになります。
| 確率既知のときは 期待値最大の戦略 |
景気 | 期待値 | 評価 | 好況 | 不況 | 0.6 | 0.4 |
|---|---|---|---|---|---|
| 私の戦略 | 積極案 | 10 | -3 | 4.8 | ←最大 |
| 消極案 | 5 | 2 | 3.8 | ||
でも期待値最大の考え方でよいのでしょうか? このようなケースが数多く起こるのであれば,平均すればこのようにするのがよいといえますが,1回しか行わないとすれば,偶然により確率の低いことが発生することもあります。「-3の事態になったら倒産する」ような場合には,このような方法は不適切です。ですから,これが「唯一の」「正しい」決定方法であり,これに従って決定「するべき」だとはいえません。しかし,これだけの条件で決定するとすれば,これ以外に合理的な説明のできる方法を示すのは困難でしょう。
期待値最大の考え方には,次のような応用ができます。ここで好況になる確率をα(不況の確率は1-α)として,双方の期待値を計算してみますと,
積極案:10α-3(1-α)=13α-3
消極案: 5α+2(1-α)= 3α+2
となります。ここで,13α-3=3α+2とすれば,α=0.5となりますので,「好況の確率が50%以上だと思うならば積極案のほうが有利になる」といえます。このようなことを知れば,意思決定をしやすくなるとも考えられますね。
相手と競争関係であるとき
零和ゲーム
これまでは,相手が景気という「自然」でした。自然は私に好意も悪意も持っていません。ここからは,競争関係にあるA社とB社を考えます。このような分野をゲームの理論といいます。まず,「A社の得はB社の損」である場合を考えますが,それを零和ゲームといいます。
下の二つの利失表はAを基準にしています。例えばケース1での左上の「3」は,A社がA1の戦略,B社がB1の戦略を採用したとき,A社は3の利益があり,B社は3の損失があるというように読んでください。
| ケース1 | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | 3 | -1 |
| A2 | 2 | 1 | |
| ケース2 | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | 1 | -3 |
| A2 | -2 | 4 | |
ゲームの理論では,AもBもこの利失表を知っており,しかも互いに最も合理的な戦略をとることも知っているとします。
では,ケース1とケース2での最適な戦略を考えてください。ケース1は簡単だと思いますが,ケース2はかなり難しくなります。☆
零和ゲームの解法
ゲーム1
たまたまAがA2を選択すると,BはA2の行のうちの最小の1にさせようとしてB2を選択します。するとAはB2の列での最大の1を得るためにA2を選択します。結局はAはA2,BはB2を選択することで落ち着きます。(A2,B2)の値1は,AとBが適切な行動をしたとき,Aが少なくとも確保できる利益であるともいえます。その値のゲームの解といい,(A2,B2)のような点を鞍点(あんてん)といいます。
| ケース1 鞍点あり |
Bの戦略 | 最小値 | B1 | B2 |
|---|---|---|---|---|
| Aの戦略 | A1 | 3 | -1 | -1 |
| A2 | -2 | 1 | 1 | |
| 最大値 | 3 | 1 | ||
ゲーム2
次のような計算方法を詳しく知る必要はありません。「ウム,なるほど」と理解してもらえれば十分です。
| ケース2 鞍点なし |
Bの戦略 | 最小値 | B1 | B2 |
|---|---|---|---|---|
| Aの戦略 | A1 | 1 | -3 | -3 |
| A2 | -2 | 4 | -2 | |
| 最大値 | 1 | 4 | ||
ゲーム2では鞍点が存在しません。AがA1を選択する確率をp,BがB1を選択する確率をqとすると,
(A1,B1)での期待値: 1pq
(A1,B2)での期待値: -3p(1-q)
(A1,B1)での期待値: -2(1-p)q
(A1,B1)での期待値: 4(1-p)(1-q)
ですから,全体でのゲームの値Vは,
V=1pq-3p(1-q)-2(1-p)q+4(1-p)(1-q)
=10pq-7p-6q+4
=10(p-0.6)(q-0.7)-0.2
となります。
ここで,もしAがp>0.6の戦略をとれば,BはVを小さくしたいのですからq=0とするでしょう。またAがp<0.6の戦略をとればBはq=1とするでしょう。そのようなことをさせないために,Aがp=0.6とすれば,Bがqをどのような値にしても,-0.2の値を確保することができます。
逆にBとしては,q>0.7とすればAはp=1,q<0.7とすればAはp=0にするので,Vは-0.2よりも大になってしまいます。それを防ぐためには,q=0.6とすればよいことになります。
結論として,AはA1を0.6,A2を0.4の確率で選択し,BはB1を0.7,B2を0.3の確率で選択することにより,ゲームの値を-0.2にすることができます。このように,戦略が確率になる場合を混合戦略といいます。なお,その方法は省略しますが,二人零和ゲームは線形計画法で解くことができます。
非零和ゲーム
下図のペイオフマトリクスの左側はAの利失で右側はBの利失です。例えばAがA1の戦略を選択してBがB1の戦略を選択したとき,Aは3の利益になり,Bは1の利益になります。このように,Aの利失とBの利失との和が0にならないモデルを非零和ゲームといいます。
| (A,B) | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | ( 3, 1) | (-1,-3) |
| A2 | (-2,-2) | ( 1, 2) | |
AとBが単独に意思決定するとすれば,その利失表は次のようになります。
Aの利失表 Bの利失表 B1 B2 B1 B2 A1 3 -1 A1 1 -3 A2 -2 1 A2 -2 2
AがA1を選択する確率をp,BがB1を選択する確率をqとすると,Aの利失表でのゲームの値VAは,
VA=3pq-1p(1-q)-2(1-p)q+1(1-q)(1-q)
=7(p-3/7)(q-2/7)+1/7
ですから,Aはp=3/7の混合戦略を選択することにより,少なくとも1/7の利益が確保できます。
同様にBについては,
VB=1pq-2(1-p)q-3p(1-q)+2(1-q)(1-q)
=8(p-1/2)(q-5/8)-1/2
より,Bはq=5/8の混合戦略により-1/2の利益を確保します。
すなわち,両者の間にどのような交渉があるにせよ,Aは1/7,Bは-1/2以上の利益がなければ交渉に応じないことになります。
では問題です。Aは両者の利失表を知っているとします。Aはどのような戦略をすればよいでしょうか? とはいうものの,やや複雑ですので真剣になる必要はありません。
ゲームの理論はかけひきに使える!
BがAの利失表を知らないとき
- Bを束縛しない
- AはBがq=5/8の混合戦略を選択ことを知っています。そのときの期待値は,
A1: 3×(5/8)-1×(3/8)=12/8
A2:-2×(5/8)+1×(3/8)=-7/8
になりますので,A1を選択することにより,1/7よりも高い利益,しかも(A1,B1)以外では最高の利益を得ることができます。 - 説得
- AはBのゲームの値-1/2を知っています。-1/2よりも高い利益を保証すれば,Bはそれに応じるでしょう。(A1,B1)をBに提示することにより,Aは3の利益を得ることができます。よしんば(A2,B2)になったとしても1/7よりも高い利益が得られます。
- 脅迫
- Bを説得するのではなく,一方的にA1を選択することをBに伝えることにより,Bは-3を回避するためにB1を選択させます。これにより間違いなく最大利益3を確保することができます。
両者が互いのペイオフ・マトリクスを知っているとき
- 脅迫
- AがA1を選択して脅迫することもできますが,逆にBがB2を選択することをAに伝えて脅迫することもできます。その点では互角ですが,Aは「自分が損失になってもかまわないのでA1を選択する。そうしたらBは重大な損失になる」と逆脅迫する手段が残っています。
- 協力
- 両者の利益合計は(A1,B1)のときが最大値4になります。交渉によりAからBにいくらかの利益を渡すことにも考えられます。その渡す額をいくらにすればよいかに関しても多様な考え方がありますが,ここでは省略します。
ゲームの理論は,単なる計算手法は実際の意思決定には役立つことは少ないでしょう。しかし,ゲームの理論の考え方はは現実社会での駆け引きの戦略に広く応用できるものです。
経営者とOR
ORの意義
コンピュータの発展により,多くの業務がシステム化され,豊富な情報が簡単に得られるようになりました。また,データウェアハウスやデータ・マイニングのような分析に便利なツールも手軽に利用できるようになりました。
しかし,間違ったアプローチをしたのでは,間違った決定をしてしまう危険があります。情報をいかに戦略に結びつけるかを合理的に考えるクセを持たないと,折角の情報が死んでしまいます。
ここで紹介した線形計画法やゲームの理論などを総称してOR(オペレーションズ・リサーチ)といいます。ORとは論理的なものの考え方であるといえます。
典型的なOR技法
ORには,いろいろな技法があります。
- PERT/CPM
- プロジェクトを納期に完成させるにはどの工程がネックになるか。コストを最小にして納期短縮するにはどの工程に資源を投入するか。
- 採算計算
- ディスカウント・キャッシュフロー法。買取とリースの損得評価。複数の投資案からの選択。最適取替問題
- 在庫問題
- 在庫を持つ費用と発注する費用とのバランス。品切れと過剰在庫のバランスなど
- 待ち行列
- レジの台数と客の流れ。機器故障と修理工の人数。駐車場の大きさなど。
しかし,型にはまった技法を用いたり,難しい数学理論を駆使することだけがORではありません。有名な例が「エレベータの待ち時間問題」があります。ある高層ビルでは,エレベータがなかなか来ないのとの不満が高まっていました。ビル管理者は,それに対処するために,エレベータ技師や統計の専門家などに依頼したのですが,その改善には多額の費用がかかることを知って悩んでいました。たまたま,ORグループに依頼したところ,解決策が見つかりました。「エレベータホールに大きな鏡をつければよい」。理由はお分かりですね?
経営者とOR
経営者が,これらの各種技法をマスターしていれば鬼に金棒ですが,なかには高度な数学知識やコンピュータツールの活用などが必要になることもあります。また実際には,現実の問題をどのようにモデル化するかは,かなりの経験と優れたセンスを必要とします。生兵法は大怪我の元になる危険もあります。
現実の問題解決には,ORの専門家に依頼するのが安全です。人手の少ない中小企業では外部のコンサルタントを起用することになりましょう。大企業であれば自社で育成することが望まれますが,その育成には優れたコンサルタントの協力を仰ぐのがよいでしょう。
しかし,これは「経営者はORなど知らなくてもよい」のではありません。ORの概要を理解しているからこそ,このような問題をORの専門家に相談しようということになるのです。最も危険なことは,ORの考え方を知らないために,間違った決定をしたり,ムダな作業をすることなのです。