グラフとは
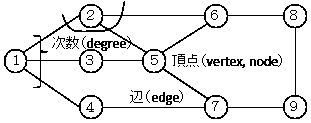
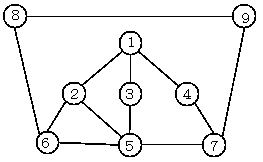
- グラフとは、〇(ノード、頂点)と、それを結ぶ ───(エッジ、辺、道)の関係を図示したものです。
- グラフ上の任意の2つのノード間にエッジが存在するグラフのことを連結グラフといいます。上図はすべて連結グラフです。
- ノードとエッジの関係が同じならば、配置が変わっても同等なグラフ(同形、isomorphic)だといいます。上左図と上中図は同形です。
- エッジに方向を示す→があるグラフ(上右図)を有向グラフ、それがないグラフ(上左図)を無向グラフといいます。
- 一つのエッジで結ばれた2つのノードは隣接している(adjacent) といいます。
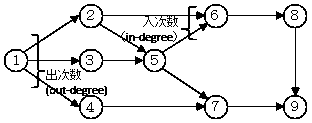
- ノードに出入りするエッジの数を次数といいます。有向グラフでは出ていくエッジ( 出辺、out-edge )の数を出次数、入ってくるエッジ(入辺、in-edge) の数を入次数といいます。
- 握手補題:次数の総和はエッジの2倍に等しい(各エッジに2つのノードがあるから)。
エッジ数=12、次数:①=3、②=3、③=2、④=2、⑤=4、⑥=3、⑦=3、⑧=2、⑨=2→24 - 奇点定理;次数が奇数のノードは偶数個存在する。①③⑥⑦
- エッジを連続した1本の線でつないだ線をパス(経路)、ループ状になる線をループといいます。

特徴のあるグラフのパターン
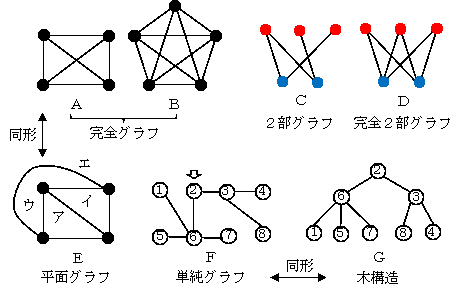
- 完全グラフ(complete graph)
全てのノードから他のすべてのノードにエッジが接続しているグラフです。
エッジ数=ノード数×(ノード数)/2 の関係があります。 - 2部グラフ(bipartite graph)
ノードを二つの部分集合(赤ノードと青ノード)に分割して各集合内のノード同士の間にはエッジがない(赤-青間のエッジだけがある)ようにできるグラフ
他のノードのすべてとエッジを持つ2部グラフを完全2部グラフという。 - 平面的グラフ (planar graph)
ノード以外の点でエッジが交差しないように平面に書けるようなグラフを平面的グラフといいます。(交差しないように実際に書いたものを平面グラフといいます)AはEに変形できます。AとEは平面的グラフですが、平面グラフはエだけになります。 - 単純グラフ(simple graph)
ループを持たないグラフ。あるノードに着眼すると木構造になる。
基本的な問題
オイラーの定理
上のグラフA、グラフBは平面グラフに変形できるか?
定理1:平面グラフにできるには「エッジ数≦3×ノード数-6」が成立する必要がある(成立しなければ平面グラフにならない。成立しても平面グラフにできるとは限らない)。
グラフA:エッジ数=6、ノード数=4 → 6≦3×4-6 →成立 →可能性あり
グラフA:エッジ数=10、ノード数=5 → 10>3×5-6 →不成立 →可能性なし
定理2:平面グラフでは、「ノード数-エッジ数+面の数=2」(一番外側の領域も一つの面とみなす)の関係がある。
上のEでは、ノード数=4、エッジ数=6、面の数=アイウエ=4 なので、上の式が成立。
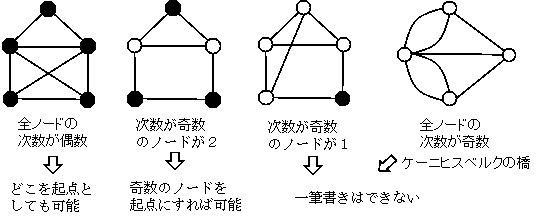
オイラーのグラフ(Eulerian graph、一筆書き)
連結グラフにおいて、すべてのエッジを一本の線でつなぐパスを作ることができるか?
ハミルトン・グラフ (Hamiltonian graph)
全てのノードを1回ずつ通って(2回以上通ってはいけない)出発点に戻るグラフはどれか?
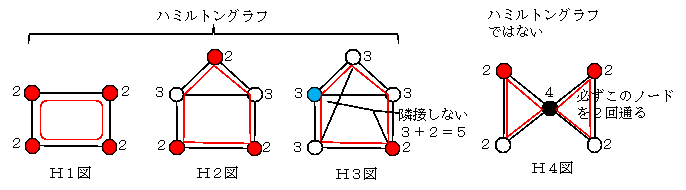
一見して、H1~H3図は赤線のように巡回できるのでハミルトングラフであり、、H4図は中央の黒ノートを左右から通るのでハミルトングラフではないことは自明であろう。
「〇〇ならばハミルトングラフである」の定理はあるが、「××ならばハミルトングラフではない」の定理は未だ存在しない。
- ディラック(Dirac)の定理:2×最小次数≧頂点数ならハミルトングラフ
H1図:頂点数=4、最小次数=2、2×最小次数≧頂点数なのでハミルトングラフである
H2図、H3図:頂点数=5、最小次数=2、2×最小次数<頂点数なのでわからない - オーレ(Ore)の定理:隣接しない任意の2ノードの次数合計最小値≧頂点数ならハミルトングラフ
H3図:隣接しない任意の2ノードとして青と赤のノードをとれば合計=5=頂点数→ハミルトングラフ
オーレの定理を満足すれば、ディラックの定理を満足する。
最大・最小問題
グラフで表現されるモデルの最大・最小問題は多くあります。その代表例を掲げます。
ここでは、直感で解ける小規模で素直な数値例ですが、一般的には「組合せ問題」という分野で、適切な解法がない、あっても計算量が膨大だという特徴があります。
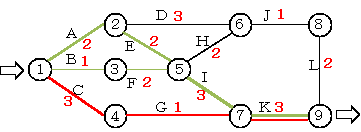
- 最短経路問題
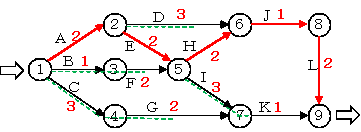
- 右のグラフでノード1からノード9へ至るまでの経路のうち、最小のノード数(エッジ数)の経路はどれか。乗換回数最小経路でもある。
赤線の経路がノード数3で最小 - 最小費用流問題
- グラフ中の赤数字は、そのエッジでの運賃である。ノード1からノード9へ至る最小運賃の経路はどれか。これを最短経路問題ということもある。
赤線の経路が3+1+3=7で最小
解法は多くありますが、最も実用的な解法の一つに動的計画法の適用があります。 - 最大流問題
- グラフのエッジは水管であり、赤数字は水管の最大流水量能力である。ノード1の水源からノード9の流出口に水を流すとき、最大量の水流はどのようになるか。ただし、ある水管に流れる水量は、それより前の水管能力の合計を超えることはできないものとする。
緑のようになる。線の太さは水量を示す。
- PERT(日程計画)
- 右の有向グラフにおいて、エッジは作業、赤数字は作業日数を示す。あるノードにおいて、入エッジのすべての作業が終了するまでは、出エッジの作業を開始することはできない。ノート1から開始し、すべての作業を終了し、9に至るまでの最短作業を求めよ。
赤線が最短日数で9日間になる。この赤線にあるエッジ(作業)に余裕がなく遅れると作業終了日数に影響し、クリティカルパスという。他の作業は緑点線になり余裕がある。
参照:PERT
- 巡回セールスマン問題( traveling salesman problem、TSP)
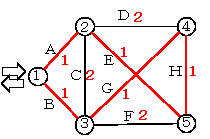
- 右のハミルトングラフにおいて、ノード1から出発し、全てのノードをただ1回だけ通過して、ノード1に戻る経路のうち、赤数字で示した運賃合計が最小になる経路を示せ。
直観的に赤線の経路が最小だとわかる。
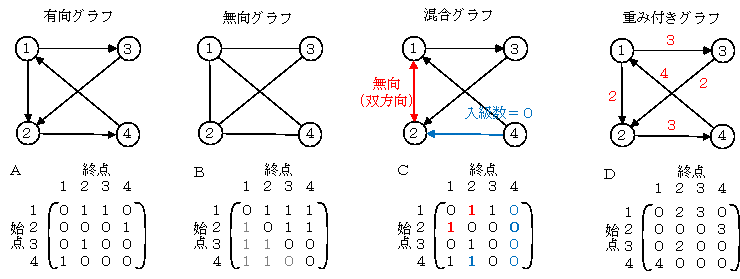
一般的な解法が見つからない問題や、解法はあるのだがあまりにも計算量が大きい問題をNP問題という。巡回セールスマン問題は、典型的なNP問題である。 - 無向グラフの隣接行列(B)は、右上と左下が対象の対象行列になります。
- 有向エッジと無向エッジがあるとき(混合グラフ、C)でも上のルールで行列を作成します(赤の部分)
- このグラフではノード4の入エッジがない(入級数=)ので、ノード4は起点になるが、他からここに到達できません。行列Cのノード4の列がすべて0になります。
- ここでは対象にしませんが、重み付けグラフのようにエッジに運賃などを与えるとき、行列(D)にその運賃を表記することにより、グラフを行列にすることができます。
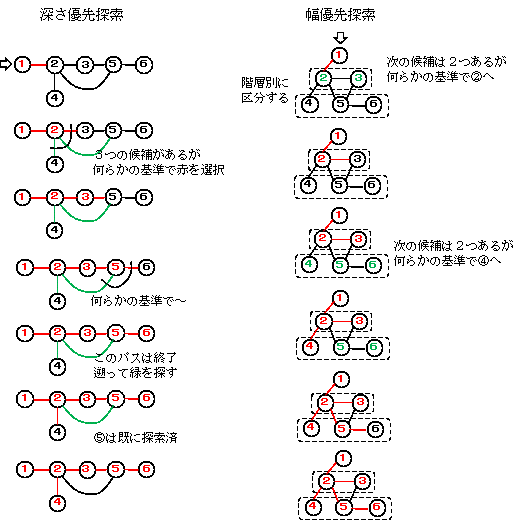
- 深さ優先探索 (depth-first search, DFS)
- ともかく適当なパスに沿って、そこにあるノードを全て探索します。その間に複数の出エッジがある場合、どれか一つを選択して先に進みます。選択しなかったエッジは記録しておきます。
パスの最後のノードを探索したら、遡って選択しなかったエッジを調べ、同様にパスの最後まで探索します。 - 幅優先探索 (breadth-first search, BFS)
- 図のように、ノードを階層別に区別しておき、その階層に含まれるノードを順に探索します。簡単なようですが、このような階層にするのが大変な作業で、あるノードに達したら、そこからのノードの階層を調べるなどの作業も発生することがあります。
隣接行列(adjacency matrix)
グラフの相隣るノードについて、エッジの始点を縦、終点を横に並べた正方行列を隣接行列といいます
・すべての要素を0にします。
・ノードiからノードjへ有向エッジがあるとき、要素 (i,j) を1にします。
・ノードiとノードjの間に無向エッジがあるとき、無向エッジは両方向の有向エッジと考えられるので
要素 (i,j) および要素 (j,i) を1にします。
ノード間の距離
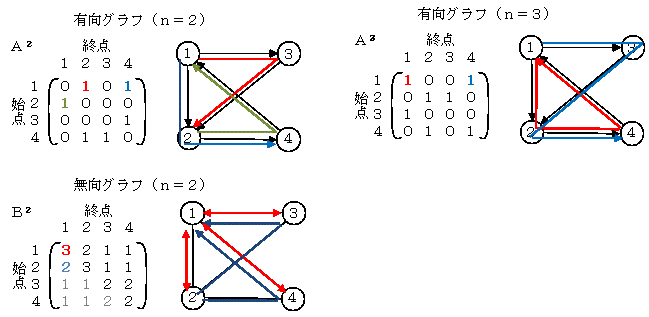
隣接行列をn乗すると,要素(i,j) の値がノードiからノードjまでのエッジ数になります。
グラフの探索
探索(search)を走査(traversal)ともいいます。条件を満足するノードのグラフでの位置(ない場合も含めて)を知ることです。配列を対象にした単純な探索に関しては「サーチ(検索)」を参照してください。
ループを持たない単純グラフは、同形の木構造に変形できます。特に級数が2の場合は、2分木になり、その探索方法は、木構造で扱っています。ここでは、ループも含む一般的なグラフを対象にします。なお、探索(search)を走査(traversal)ともいいます。
実際の探索手順は、ループがあるし、無向・有向の違いもあり、木構造での探索と比べてかなり複雑です。ここでは理論的な説明は省略して、イメージだけを示します。
探索に成功した時点で打ち切るのですが、ここでは、全てのノードを探索しています。