最短経路問題の説明
図のような道路があります。①から⑥までの最短経路を求めます。いくつかの解法がありますが、ここでは代表的なダイクストラ法を簡便化した方法を用います。
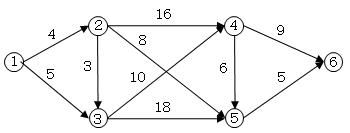
終点から始点まで戻るように考えます。
地点iから直接に行ける地点jまでの距離を C(i,j) とします。
地点iから終点までの最短距離を D(i) とします。
最短にするためには、地点iから地点Kに行けばよいとき、Pnext(i) =Kとします。
i=6のとき、
⑥は終点なので、
D(6) =0
Pnext(i) は定義する必要はない。
i=5のとき、
⑤から出ていく道は「⑤→⑥」だけです。そして、⑥は終点ですから、
D(5) = C(5,6) =5
Pnext(5) =6
i=4のとき、
④から出ていく道は「④→⑥」と「④→⑤」の2本があります。
「④→⑥」のとき、A = C(4,6) = 9
「④→⑤」のとき、B = C(4,5)+D(5) = 6+5=11
A<Bなので、
D(4) = 5
Pnext(5) =6
このようにして、i=1まで行うと、次の表ができます。
i D(i) Pnext(i)
6 0 -
5 5 6
4 9 6
3 19 4
2 13 5
1 17 2
これから、最短距離は17になります。
最短経路は、次の手順で求めます。始点①から始めます。
Pnext(1) =2 ②へ行く。
Pnext(2) =5 ⑤へ行く。
Pnext(5) =6 ⑥へ行く。
⑥が終点なので、最短経路は
1→2→5→6
定式化
地点の個数をNとし、地点番号をi、終点の地点番号を Nlast(=N)とします。
i=Nlast のとき、
D(Nlast) =0
i<Nlast のとき、
iを一つずつ減らして1になるまで行う。
D(i) =min{ D(k) + C(i,k)}
k=i+1,i+2,・・・,N で C(i,k)が存在するもの
Pnext(i) = minとなるkの値
計算プログラム
カーナビゲーションでの応用
カーナビの主機能は、現在地から目的地への最短経路を求めることです。複雑な道路網などで膨大な地点数、経路数があるので、計算量を少なくすることが求められます。その代表的な手法に、上述のダイクストラ法をベースとした hub labeling法があります。その概要を示します。
- あらかじめ、地域別あるいは幹線別に、主要地点間の最短経路を計算した表をもっています。
- 主要地点Aから主要地点Bの最短経路を求めるには、いくつかの中継地点を経由したAからBへの経路候補を探します(上の図が得られます)。主要地点間に絞っているので、規模は小さくなっています。
- その図を用いた計算により、主要地点Aから主要地点Bの最短経路が得られます。
- 現在地と目的地が主要地点になっていればここまでの処理で完了ですが、そうでない場合は現在地とA、目的地とBの間の最適経路を求め上の最適距離に加えますが、このときもどのA、Bを選ぶかで最適計算をすることになります。