Web教材一覧>
ハードウェアとソフトウェア
木構造
キーワード
木構造、2分木、2分探索木、ヒープ
- 木構造
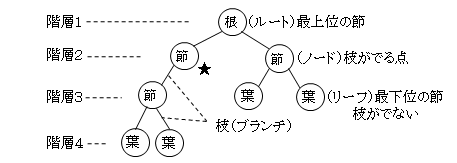
- 木構造(ツリー構造)とは、データの階層構造の一つで、図のように木を逆にしたように形式になります。根(ルート)、節(ノード)、葉(リーフ、要素)には、データが対応しています。
- 順序木
- 葉が一定の順序で並ぶように節が設定されている木のことです。木構造は、通常は順序木になるよう生成されます。
- 探索木
- 葉の探索が容易になるよう設計された木です。順序木とほぼ同じです。
各葉へのアクセスは、根からたどることになります。それを二分木を走査(トラバース)するといいます。
2分木での探索の方法
・幅優先探索:同じ階層を左から右へ走査
・深さ優先探索:先に一つの葉まで到達してから親へ戻る
・先行順(行きがけ順):根→左の部分木→右の部分木 の順に走査
・後行順(帰りがけ順):左の部分木→右の部分木→根 の順に走査
・中間順(通りがけ順):左の部分木→→根右の部分木 の順に走査
- 2分木
- 特に、節から出る枝が2本の場合(データの関係によっては、★印のように枝が1本の場合もあります)を2分木(バイナリツリー)といいます。
- 2分探索木
- さらに、データのキー項目の大小により並べておき、探索を容易にした構造を、2分探索木といいます。この場合、
左の子 < 親 < 右の子
となるようにします(なお、データの特徴や探索の用途によっては、これとは異なる規則にする場合もあります)。
以降の説明は「深さ優先探索 先行順」を用いています。
- 2分探索木の更新
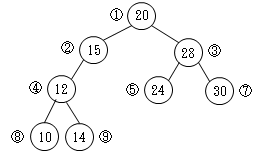
- 上図において、「左の子 < 親 < 右の子」の規則に従いながら、データの挿入や削除を行うことを考えます。
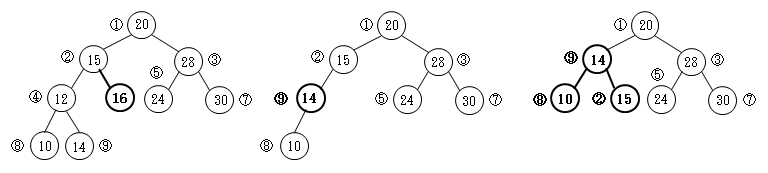
- 値が15のデータを挿入
①の20と比較すると小さいので、②と比較します。②よりも大なので「右の子」になります。下左図になります。
- ④(12)を削除
単に④を外して、②から⑧と⑨をつないだのでは、②(15)<⑨(14)になってしまい、規則に反します。下中図のようにする必要があります。
さらに、②と⑨を入れ替えて下右図にするのは、単なる更新ではなく再編成であると考えるのが妥当でしょう。
- 2分探索木による探索回数
- 更新以前の図で、X=14のデータを探索する場合は、次のようになります。
- ルート①と比較する。X<①なので、左の子②へ
- X<②なので、左の子④へ
- X>④なので、右の子⑨へ
- X=⑨なので、検索終了
X=16(存在しない)の場合
- ルート①と比較する。X<①なので、左の子②へ
- X<②なので、右の子へ行きたいのだが存在しないので、検索終了
このように、最大4回(すなわち階層の深さ)の比較で検索することができます。
(なお、ここではルートから探索していますが、最も階層の深い節からスタートしたり、最も離れた節からスタートするなど、多様な探索方法があります)
- 2分探索木とリスト構造
- 木構造を、そのままファイルに実装することはできません。図のように、左側の子、右側の子のデータが格納されているポインタを持つリスト構造にして、表のような配列にして格納します。
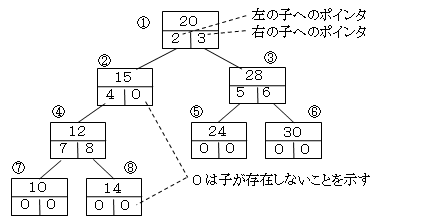 格納 左の子への 自分の 右の子への
格納 左の子への 自分の 右の子への
ポインタ ポインタ キー値 ポインタ
1 2 20 3
2 4 15 0
3 5 28 6
4 7 12 8
5 0 24 0
6 0 30 0
7 0 10 0
8 0 14 0
- 完全2分木
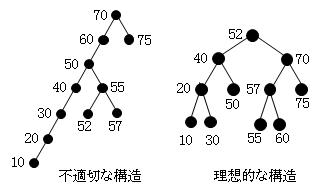 「70→60→50→40→30→20→10→55→52→57→75」の順序でデータが出現し、そのまま2分木にすると、左の「不適切な構造」のようになります。これではX=10を探すには、7回の比較が必要になります。それに対して「理想的な構造」にすれば4回の比較ですみます。探索を最適にするには、根から各葉までの高さができるだけ等しくすることが求められます。
「70→60→50→40→30→20→10→55→52→57→75」の順序でデータが出現し、そのまま2分木にすると、左の「不適切な構造」のようになります。これではX=10を探すには、7回の比較が必要になります。それに対して「理想的な構造」にすれば4回の比較ですみます。探索を最適にするには、根から各葉までの高さができるだけ等しくすることが求められます。
そのような2分木を完全2分木といいます。完全2分木の場合、節の個数Nと階層Mの間には、
N=1+2+22+ … +2M=2M+1
M=log2(N+1)-1
の関係があります。すなわち、探索に要する計算量のオーダーは、O(logN) になります。挿入や削除に要する計算量も同じです。
完全2分木にするには、木構造を作成するときに、データの全体を小さい順に並べて、
全体の中央値をルートにする
左側半分のうちの中央値を左の子にする
右側半分のうちの中央値を右の子にする
ことを繰り返すことにより作成できます。
しかし、その後、追加や削除を繰り返すうちに、次第に「理想的な」状態からずれたものになってしまいます。それで、処理効率を改善するために、必要に応じて木構造を再編成することがあります。- ヒープ
- 完全2分木を配列で表現するデータ構造をヒープといいます。ヒープを用いた探索のことをヒープ探索、ソートのことをヒープソートといいます。ヒープ探索の計算量は O(logN) 、ヒープソートの計算量は O(N logN) になります。
- 演算木
- 数式を2分木で表現することができます。それを演算木といいます。一般の数式表現を2分木で表現して、逆ポーランド記法にすることができます。
例えば、数式 A+B×(C+D)+E は、演算の優先順位を( )で明示すれば、
((A+(B×(C+D)))+E)
になります。
最も深い( )を、演算子を親の節、被演算数値を左の葉、演算数値を右の葉とする部分木にします。それを組み合わせると演算木ができます。そして、この演算木を葉のほうから後行順に表記すると、
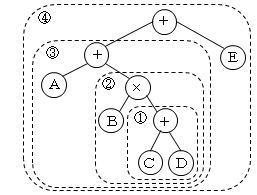 ((A+(B×(C+D)))+E)
((A+(B×(C+D)))+E)
└─①─┘
CD+
└───②───┘
BCD+×
└─────③─────┘
ABCD+×+
└─────④─────────┘
ABCD+×+E+
となり、逆ポーランド記法の
ABCD+×+E+
になります。
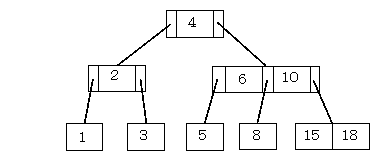
- B木(バランス木)
- 木構造を発展させたデータ構造にB木やB+木があります。これらは、データベースに広く用いられています。
B木は、多分岐の平衡木(バランス木)です。挿入・検索・削除が効率的に行えることが特徴です。
B木では、データの分岐先がすべて同一の階層に属しており、葉を除いた全ての節が一定数以下の分岐枝をもち、その先が分岐した元の枝よりも少ない分岐を持っている特徴があります。一つのノードから最大m個の枝が出るとき、これをオーダーmのB木といいます。
- B+木
- B+木は、B木を発展させたもので、B木と異なり、
・データ格納先のアドレスを末端の葉(リーフ)のみに格納する
・リーフ(葉)とリーフ(葉)を結ぶポインタを設ける
・木の深さ(たどるルートの数)が一定
の特徴があります。
B+木では次数dが木構造内のノードの容量の尺度になります。d <= m <= 2 d の関係がありmす。例えば、次数3のB+木では、根ノード以外の内部ノードは3個から6個のキーを格納し、各内部ノードは、 d+1(=4)~2d+1(=7) 個の子ノードを持ちます。
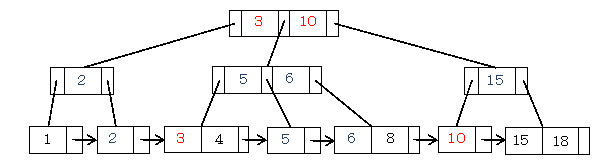
次数をd、木の高さをhとすると、葉の最大数Nは N=dh ですから、h=logd となります。すなわち、検索などでのアクセス回数(計算量、オーダ)はO(logN) になります。
なお、説明は省略しますが、B+木はデータをブロックというかたまりで操作するのに適しており、データをHDDなどの大容量記憶に保持する大規模データベースで採用されています。
 格納 左の子への 自分の 右の子への
格納 左の子への 自分の 右の子への 「70→60→50→40→30→20→10→55→52→57→75」の順序でデータが出現し、そのまま2分木にすると、左の「不適切な構造」のようになります。これではX=10を探すには、7回の比較が必要になります。それに対して「理想的な構造」にすれば4回の比較ですみます。探索を最適にするには、根から各葉までの高さができるだけ等しくすることが求められます。
「70→60→50→40→30→20→10→55→52→57→75」の順序でデータが出現し、そのまま2分木にすると、左の「不適切な構造」のようになります。これではX=10を探すには、7回の比較が必要になります。それに対して「理想的な構造」にすれば4回の比較ですみます。探索を最適にするには、根から各葉までの高さができるだけ等しくすることが求められます。 ((A+(B×(C+D)))+E)
((A+(B×(C+D)))+E)
