キューとスタック
──┐ push ──┐ ┌─→ pop
│ │ │
： │↓ │ │↓ ││
├────┤ ├────┤ ┌────┐
１１│データ５│ ０│データ５│ ０│データ１│
├────┤ ├────┤ ├────┤
１２│データ４│ １│データ４│ １│データ２│
├────┤ ├────┤ ├────┤
１３│データ３│ ２│データ３│ ２│データ３│
├────┤ ├────┤ ├────┤
１４│データ２│ ３│データ２│ ３│データ４│
├────┤ ├────┤ ├────┤
１５│データ１│ ４│データ１│ ４│データ５│
├────┤ ├────┤ ├────┤
： │ ││ ：│ │ ：│↑ ││
│ │ │
└─→ push ──┘ └─→ pop
キュー スタック スタック
ＦＩＦＯ ＬＩＦＯ （Javascriptでのイメージ）
配列の特殊な構造に、キューとスタックがあります。
キューは、ＦＩＦＯ（First In First Out：先入れ先出し）方式で、待ち行列ともいいます。プリンタへのスプールによる出力処理やデータを入力された順番通りに処理するときなどに用いられます。
それに対して、スタックは、ＬＩＦＯ（Last In First Out：後入れ先出し）方式です。新しいデータを入れる（Push）と、それまでのデータが下に押し下げられ、取り出すとき（Pop）ときは、１番上のデータが取り出され、２番目以降のデータが上に押し上げられます。
スタックの実験
Javascriptでは、データの入る配列名を「スタック」とすれば、push, popは、
スタック.push(データ); スタック.pop();
の形式で記述します。
しかし、Javascriptでは、配列の末尾にpushし、末尾要素をpopする仕様になっているので、後入れ先出しであることは同じですが、むしろ上右図のようなイメージになります。
適宜、push, popを行ってください（clearはスタックを空にする操作 stack = []; です）。
スタックの利用
コンピュータでは、スタックが広い分野で用いられています。
- ＣＰＵでは、命令を実行するためのレジスタの一つとして、スタックポインタというレジスタを用いています。
- コンパイラが数式を命令に展開する技法の一つに「逆ポーランド記法」がありますが、これにはスタックが重要な役割を持っています（これに関しては後述します）。
- 再帰呼び出しを実現するには、スタックが用いられます。
- 複雑な探索問題や最適化問題では、分枝限定法がとられますが、その中間結果を記録する手段（バックトラッキング）として、スタックが用いられます。
逆ポーランド記法との関係
- 逆ポーランド記法
- 数学の一般的な記法での数式 Ａ＋Ｂ×Ｃ を計算するには、発生順序により「(Ａ＋Ｂ)×Ｃ」とするのは誤りです。日本語では「ＡにＢにＣを×したものを＋する」ことになりますが、その順に「ＡＢＣ×＋」と記述する記法を逆ポーランド記法といいます。
もう少し複雑な例にして、数式を逆ポーランド記法にする手順を説明します。
数式 Ａ＋Ｂ×（Ｃ＋Ｄ）＋Ｅ は、演算の優先順位を（ ）で明示すれば、
（（Ａ＋（Ｂ×（Ｃ＋Ｄ）））＋Ｅ）
になります。
最も深い（ ）から、数式を逆ポーランド記法に置き換えていきます。
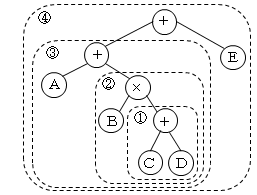（（Ａ＋（Ｂ×（Ｃ＋Ｄ）））＋Ｅ）
└─①─┘
ＣＤ＋
└───②───┘
ＢＣＤ＋×
└─────③─────┘
ＡＢＣＤ＋×＋
└─────④─────────┘
ＡＢＣＤ＋×＋Ｅ＋
となり、逆ポーランド記法の
ＡＢＣＤ＋×＋Ｅ＋
になります。
なお、これを木構造（演算木）を用いて表現することもできます。
練習問題
問題１： (Ａ＋Ｂ)×(Ｃ－Ｄ) → ＡＢ＋ＣＤ－×
問題２： Ａ／(Ｂ－Ｃ)＋Ｄ → ＡＢＣ－／Ｄ＋ - スタックによる計算方法
- 数学での記法を逆ポーランド記法に変換すれば、スタックを利用して簡単に計算することができます。
そのルールは、次の通りです。
逆ポーランド記法で記述した数式を左から順番に処理する。スタックは空である。
数値ならば、スタックに Push する
演算子ならば、
スタックの１番上の数値を Pop して、その数値をＸとする。
新しくスタックの１番上にきた数値をＹとして、ＹにＸを演算する。
その結果をＹに代入する。
数式がなくなったとき、スタックには唯一の数値が残っており、それが数式の結果である。
このように、逆ポーランド記法では、＋×や（ ）などの優先順位を考慮する必要がなく、式の解釈が簡単になり、スタック操作だけで行えるので、初期の電卓では逆ポーランド記法の順に入力するものもありました。また、コンパイラで数式を解釈するときにも利用されています。 - 例題
- 「ＡＢＣ／－」を例にして説明します。
Step1：Ａを Push する。
Step2：Ｂを Push する。
Step3：Ｃを Push する。
Step4：／になった。Ｃが Pop され、スタックの最上段がＢになる。
最上段の値を Ｂ／Ｃ の計算結果に置き換える。
Step5：－になった。Ｂ／Ｃ が Pop され、スタックの最上段がＡになる。
最上段の値を Ａ－(Ｂ／Ｃ) の計算結果に置き換える。
数式がなくなったので、計算結果は Ａ－(Ｂ／Ｃ) となる。
スタックの状況は、次のようになります。
Step1 Step2 Step3 Step4 Step5
Ａ Ｂ Ｃ ／ －
┌───┬───┬───┬───┬──────┐
０ │ Ａ │ Ｂ │ Ｃ │Ｂ／Ｃ│Ａ－(Ｂ／Ｃ)│
└───┼───┼───┼───┼───┬──┘
１ │ Ａ │ Ｂ │ Ａ │ └ 計算結果
└───┼───┼───┘
２ │ Ａ │
└───┘ - 実験
逆ポーランド記法の数式を与えて数学記法に変換します。変数は英字１文字とします。
・数学記法で（ ）が煩雑についていますが、プログラムを単純にしたからです。
・下記のｋと例題の番号が逆になっている理由は、上述「スタックの実験」を参照してください。