ご利用にあたって
多変量解析は、多くの統計技術を組み合わせた応用分野でもあり、AIのデータ処理技術の基盤技術でもあり、その活用が盛んになっています。
それだけ複雑な処理ですので、素人が JavaScript のような言語で独自開発するのは不適切です。
実務的には、統計分野の言語である Python や R での オープンソースのパッケージを利用するとか、
単純なケースでは Excel を使うのが適切です。
ここに掲げた関数は、私が手法を理解するために作成したものであり、そのような利用だけに限定してください。
参照:「多変量解析の基礎」
多変量解析のデータでは、多様な尺度の系列データを対象にします。
系列データの項目は、成績[5段階評価]、試験の点数[点]、勉強時間[時間]など単位が異なり、それにより数値の大きさも様々です。
系列間で値の大小が大きく異なると、大きな系列の影響が大きくなる(見える)ことが発生します。
それを回避するために、入力データを平均0分散1の値に標準化することがあります。
xs = (x - μ) / σ(分散は自由度ではなく標本数で割っています)
簡単な処理ですが、使う機会が多いので関数にしました。
(以下の関数の多くは、説明を容易にするために、このプロセスは省略しています。)
入力 標本→
var x = [ [ 3000, 1000, 2000, 4000, 5000], ↓系列
[ 0.01, 0.05, 0.03, 0.02, 0.04],
[ -3, 8, 5, 7, -2] ];
var [ xs, μ, σ ] = maStd(行列);
出力
xs[0][0]=0 xs[0][1]=-1.414 xs[0][2]=-0.707 xs[0][3]= 0.707 xs[0][4]= 1.414
xs[1][0]=-1.414 xs[1][1]= 1.414 xs[1][2]= 0 xs[1][3]=-0.707 xs[1][4]= 0.707
xs[2][0]=-1.303 xs[2][1]= 1.086 xs[2][2]= 0.434 xs[2][3]= 0.869 xs[2][4]=-1.086
μ[0]=3000 μ[1]=0.03 μ[2]=3
σ[0]=1414 σ[1]=0.014 σ[2]=4.604
多くの統計関係の関数は、データを [特性][標本] の形式で扱いますが、実務上ではリレーショナルデータベースやスプレッドシートのように [標本][特性] の形式でもち、行名や列名も持つのが一般的です。その形式をここではデータフレーム形式といいます。
maDfMtx(df)は、データフレーム形式のデータを [特性][標本] の形式に変換します。
簡単な処理ですが、毎度記述するのが面倒なので関数にしました。
入力 ケース2のデータを行列形式で与えます。
「*」の項は、ダミーで任意の値でかまいませんが必須です。
行名┐
var df = [ [ "*", "国語", "英語", "数学"], // 列名
[ "A", 3, 5, 3 ],
[ "B", 4, 3, 5 ],
[ "C", 3, 4, 5 ],
[ "D", 5, 3, 4 ],
[ "E", 5, 5, 3 ] ];
var rtn = maDfMtx(df);
出力
rtn["行列"] [ [ 3, 4, 3, 5. 5 ], // 国語 ┐
[ 5, 3, 4, 3, 5 ], // 英語 ├転置行列
[ 3, 5, 5, 4, 3 ] ] // 数学 ┘
rtn["行名"] ["A", "B", "C", "D", "E"]
// ★あえて「行」名、「列」名は df での「行」「列」のままにしてある
rtn["列名"] ["国語","英語","数学"] // (その後の処理で df を用いることが多いので)
rtn["共分散行列"]
rtn["相関行列"]
入力
標本 x[*][k]
var x = [[12, 20, 24, 26, 33], ┐
[ 3, 6, 7, 10, 14], ├ 系列 x[i][*]
[22, 16, 14, 19, 8]]; ┘
var rtn = maCovcor(x);
出力
rtn["共分散行列"]
[[ 60, 31.5, -34.75],
31.5, 17.5, -17.5],
-34.7, -17.5, 28.2]]
rtn["相関行列"]
[[ 1, 0.972, -0.844],
[ 0.972, 1, -0.787],
[-0.844, -0.787, 1 ]]
多変量解析では重回帰式の作成が多用されますが、それには連立方程式の解を求める必要があります。
入力
被説明変数
var y = [ 18, 12, 14, 6, 12, 8, 10, 16 ];
説明変数
var x = [ [ 8, 7, 5, 4, 6, 2, 3, 9 ],
[ 4, 7, 8, 3, 8, 5, 6, 9 ],
[ 8, 7, 9, 3, 8, 3, 6, 7 ] ];
var 係数 = maMregEq(y, x)
出力
係数[i]
[0] = 2.504
[1] = 0.816
[2] = -0.275
[3] = 1.055
y = 2.504 + 0.816 x[0] - 0.275 x[1] + 1.055 x[2]
主成分分析や因子分析など多変量解析の解法では、相関行列や共分散行列から固有値・固有ベクトルを求める局面が多くあります。
直接に固有値を求めるには、変量の個数をnとすると、n次方程式の実根を求めることになるので複雑です。
しかし、多変量解析では次の特徴があります。
・行列が対称行列であること
・実務的には、すべての固有値ではなく、大きい固有値を2、3個得ればよい
この特徴を用いた解法のうち、ここではべき乗法(Power Method)による近似解を得る方法を用います。
入力 対称行列
var a = [ [ 1, 0.376, -0.097 ],
[ 0.376, 1, -0.359 ],
[ -0.097, -0.359, 1 ] ];
var rtn = maEigenPower(a);
出力
固有値(λ[i] ) 固有ベクトル(V[i][j])
[0] = 1.570 [0][0] = 0.541 [0][1] = 0.674 [0][2] =-0.504
[1] = 0.902 [1][0] = 0.675 [1][1] =-0.006 [1][2] = 0.738
[2] = 0.526 [2][0] =-0.495 [2][1] = 0.739 [2][2] = 0.457
対称行列なので右上半分だけでよい。
上述の maRegEq は。回帰式の係数を求めるだけでしたが、ここでは重回帰分析全体をカバーします。
算出データ量が大量、複雑になるので、Return では予測変数を無視し、戻り値は回帰式の係数と分散分析表の主要項目に限定します。
処理手順
1 一般統計処理:共分散行列、相関行列、2への各要素の算出
2 重回帰式の算出;連立方程式の定式化と解(重回帰式の係数)、実測値との比較
予測変数がある場合の予測値の計算
3 重回帰式の信頼性の検定
4 各係数の信頼性の検定
入力
被説明変数
var y = [ 18, 12, 14, 6, 12, 8, 10, 16 ];
説明変数
var x = [ [ 8, 7, 5, 4, 6, 2, 3, 9 ],
[ 4, 7, 8, 3, 8, 5, 6, 9 ],
[ 8, 7, 9, 3, 8, 3, 6, 7 ] ];
予測変数 説明変数と同じ構成、省略可 // Return のときは与えない
var xp = [[ 5, 6],
[ 3, 4],
[ 6, 5] ];
呼出
var [係数, 分散分析表] = maReg(被説明変数, 説明変数)
出力
係数
[0] = 2.504, [1] = 0.816, [2] = -0.275, [3] = 1.055
y = 2.504 + 0.816 x[0] - 0.275 x[1] + 1.055 x[2]
分散分析表
自由度 変動 分散 分散比 有意水準0.01 有意水準0.05
回帰 [0] dfr=3 [3] Sr=93.413 [6] Vr=31.13 [8] F=6.701 [9] f1=16.69 [10] f5=6.591
残差 [1] dfe=4 [4] Se=18.587 [7] Ve=4.647
合計 [2] dft=7 [5] St=112.00
rtn['係数'] 判別関数の係数
rtn['判別値'] 入力データの判別関数による判別値
rtn['評価表'] 教師による判別値と判別関数による判別値の一致度
ここでの判別分析は、いくつかの特性を持つ標本がA群(1)とB群(-1)のいずれに属するかのデータを与えて、その判別をする関数を見つけることとします。
判別分析には、
線形判別関数による判別分析
マハラノビス距離による判別分析
が主流ですが、ここでは前者を扱います。
しかも、ごく単純に重回帰式を求めて、それを判別関数として、与えた群区分値と判別関数から求めた評価値を比較して
一致・不一致の件数を表示するだけにします。
入力 1標本を1行とする形式にするのが通常です。
群 特性
var Df = [ [ 1, 3, 8, 4 ], // ↓標本
[ -1, 6, 2, 6 ],
[ 1, 6, 7, 6 ],
[ -1, 8, 6, 4 ],
[ -1, 7, 3, 5 ],
[ 1, 4, 7, 3 ],
[ 1, 6, 3, 6 ],
[ -1, 7, 5, 8 ],
[ , 3, 8, 4 ], // ↓予測 群を与えない
[ , 6, 2, 6 ] ];
var rtn = maLda(df);
出力
rtn["係数"] :判別関数の係数
rtn["判別値"]:標本、予測の判別関数の値
rtn["評価表"]:一致度の表
上述の maLda(線形判別関数による判別分析)は、単に2点間の距離を対象にしていましたが、マハラノビス距離は、データの相関関係を考慮した上で距離を算出します。
そして、対象の標本がA群・B群に属しているとしたときの距離DA、DBを算出します。そして、DA<DBならばA群、DA<DBならばB群と判定します。
戻り値 rtn[i][j] は、iは標本番号でjは次の意味です。
rtn[i][0]:DAの値
rtn[i][1]:DBの値
rtn[i][2]:判別結果 DA<DB→ 1、DA>DB→ -1
rtn[i][2]:不一致 判別結果が入力での群と異なれば "*"にする。一致の場合は ""
入力 1標本を1行とする形式にするのが通常です。
標本名 群 特性
var Df = [ ["A", 1, 3, 8, 4 ], // ↓標本
["B", -1, 6, 2, 6 ],
["C", 1, 6, 7, 6 ],
["D", -1, 8, 6, 4 ],
["E", -1, 7, 3, 5 ],
["F", 1, 4, 7, 3 ],
["G", 1, 6, 3, 6 ],
["H", -1, 7, 5, 8 ],
["I", , 3, 8, 4 ], // ↓予測
["J", , 6, 2, 6 ] ];
var rtn = maMts(df);
出力
rtn[i][0] rtn[i][1] rtn[i][1] rtn[i][1]
2.25 992.08 1
4.12 2.25 -1
2.25 129.75 1
28.13 2.25 -1
7.13 2.25 -1
2.25 629.08 1
2.25 9.75 1
5.51 2.25 -1
2.25 992.08 1
4.12 2.25 -1
手順
1 入力データをデータフレーム形式で与え、転置行列 mtx[系列][標本] を生成する。maDfMtx(df) 利用
以降 x[i][j] の i は系列番号、j は標本番号となる。
系列別平均 μx[i] を算出
2 mtx から、相関行列 cor [系列][系列] を生成する。maCovcor(x) 利用
3 相関行列の大きい3つの固有値と固有ベクトル λv[k][j] を求める。maEigenPower(cor) 利用
以降が本関数での主処理
4 主成分の式 Fx[k] を生成する λv[k][j] とμx[i]が関係
Fx[k] = Σ(λv[k][i]*(x[i][j]-μx[i])) i = 0~系列、k=0~2(因子)
5 各標本の特性値 x[i][j] を Fx[k] に代入。各標本の主成分得点[j][k] を求める。
この際、主成分の得点のばらつきを解消するため、平均0、分散1の標準化を行う。
主成分の2つを選びX軸Y軸とし、各標本の主成分得点をプロットすれば主成分分析図ができる。
参照:「主成分分析」(Python)
rtn の内容
rtn['系列別平均'] μx[i]
rtn['固有ベクトル'] λv[k][i]
// 上の2つから 主成分への変換式 Fx[k] の定式化ができる。
rtn['主成分得点']
入力
↓標本 系列→
var df = [ [ "*", "P", "Q", "R" ],
[ "A", 8, 9, 4 ],
[ "B", 2, 5, 7 ],
[ "C", 8, 5, 6 ],
[ "D", 3, 5, 4 ],
[ "E", 7, 4, 9 ],
[ "F", 4, 3, 4 ],
[ "G", 3, 6, 8 ],
[ "H", 6, 8, 2 ],
[ "I", 5, 4, 5 ],
[ "J", 6, 7, 6 ] ];
var rtn = maPca(df);
出力
rtn['系列別平均'] μx[i]
5. 2, 5. 6, 5. 5
rtn['固有ベクトル'] [k][i]
0.540, 0.673, -0.503
0.674, -0.005, 0.737
-0.495, 0.739, 0.456
rtn['主成分得点'] [j][k]
0.783, 0.206, 0.229
-0.496, -0.283, 0.947
… … …
-0.160, -0.133, -0.680
0.193, 0.243, 0.449
クラスタリングには、階層型と非階層型に分類されますが、ここでは非階層型の代表的なk-meansを用います。
標本A~Jを、特性の似ているグループ分けします。そのグループ(群)数を指定する必要があります。
単に各群の中心点から近い標本をその群に属するとするだけで、各特性の影響を分析するプロセスは省略しています。
入力
var Df = [ [ "*", "c0","c1","c2","c3","c4"],
[ "A", 6, 6, 6, 4, 4 ],
[ "B", 5, 6, 4, 5, 6 ],
[ "C", 6, 6, 7, 4, 5 ],
[ "D", 5, 5, 6, 5, 4 ],
[ "E", 6, 6, 7, 6, 4 ],
[ "F", 6, 6, 5, 5, 6 ],
[ "G", 4, 4, 3, 6, 5 ],
[ "H", 5, 5, 4, 4, 5 ],
[ "I", 4, 5, 5, 5, 6 ],
[ "J", 3, 4, 4, 5, 4 ] ];
var 群数 = 2;
var 群 = maClusterKM(df, 群数);
出力
A B C D E F G H I J
0, 1, 0, 0, 0, 0, 1, 1, 1, 1
「行iと行kの距離が最小のとき、iとjを同一のグループとする」ことを、全体が1つのグループにまるまで繰り返します。
初期値設定
次の処理を群数>1の間繰り返す。
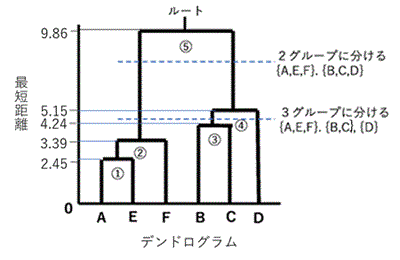
次の結果が得られたとします。これを図示すると右図(デンドログラム)になります。
最短距離[1]=9.86 グループ[1]={A,E,F,B,C,D},
最短距離[2]=5.15 グループ[2]={A,E,F},{B,C,D},
最短距離[3]=4.24 グループ[3]={A,E,F},{B,C},{D},
最短距離[4]=3.39 グループ[4]={A,E,F},{B},{C},{D},
最短距離[5]=2.45 グループ[5]={A,E},{B},{C},{D},{F},
入力
var Df = [ [ "", "c0", "c1", "c2", "c3", "c4"], // 計算には用いない
[ "A", 2, 9, 8, 3, 8 ],
[ "B", 6, 3, 3, 7, 9 ],
[ "C", 9, 5, 4, 9, 9 ],
[ "D", 8, 4, 1, 6, 5 ],
[ "E", 1, 9, 9, 3, 6 ],
[ "F", 4, 7, 8, 2, 7 ] ];