スタートページ> JavaScript> 他言語> Python 目次> ←散布図 →主成分分析
keyword:基本統計量、共分散、回帰直線、相関係数、信頼区間、t分布、重相関
np.cov()、df.corr()
ライブラリ;scikit-learn(sklearn)、linear_model、linear_model.LinearRegression()
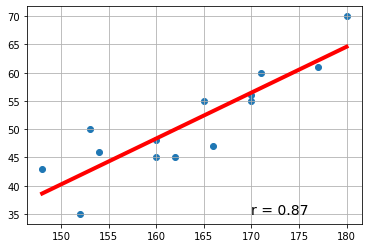
下記の青線の部分をGoogle Colaboratryの「コード」部分にコピーアンドペースト(ペーストは Cntl+V)して実行すれば、右図の画像が表示されます。
例1:回帰直線 y=a+bx や相関係数を計算するプロセスを示します。

import numpy as np
import matplotlib.pyplot as plt
# 入力データ
x = np.array([180,170,162,171,160,165,148,153,170,154,160,166,177,152])
y = np.array([ 70, 55, 45, 60, 45, 55, 43, 50, 56, 46, 48, 47, 61, 35])
# ====================================== 基本統計量の計算
n = len(x) # 組数:n= 14
mx = x.mean() # 平均:mx=163.4
my = y.mean() # my=51.14
sxx = np.sum((x-mx)**2) # 偏差平方和:sxx=sum((x-mx)**2)=1203.43
syy = np.sum((y-my)**2) # syy=sum((y-my)**2)=1041.71
vx = sxx/n # 標本分散:vx=sxx/n=85.96
vy = syy/n # vy=syy/n=74.41
# ======================== 共分散 sxy
sxy = np.sum((x-mx)*(y-my)) / n
# 共分散A(標本分散による):sxy = np.sum((x-mx)*(y-my))/n=69.795
# ========= 注 np.cov による共分散
npcov = np.cov(x, y) # 共分散行列B(np.covによる):cov = np.cov(x, y)=
# [[92.57142857 75.16483516]
# [75.16483516 80.13186813]]
cov = npcov[0,1] # 共分散Bのxy要素 cov = npcov[0,1]=75.16
# 共分散Bは不偏推定量 自由度(n-1)を用いているため共分散Aと異なる
# cov*(n-1)/n cov=69.795 と修正すると共分散Aと一致する
# ======================== 回帰直線 y = a + bx の計算
b = sxy / vx # b = sxy/vx= 0.812
a = my - b*mx # a = my-a*mx= -81.56
print('回帰直線:y =', a, ' + ', b, '*x') # y = -81.56 + 0.812*x
# ======================= 相関係数 r
r2 = (sxy/vx)*(sxy/vy) # 決定係数:r2=(sxy/vx)*(sxy/vy)=0.76
r = np.sqrt(r2) # 相関係数:r = ±sqrt(r2) =0.87
if b < 0:
r = -r # 回帰直線が右上がりなら+、右下がりなら-
# ====================================== 散布図の表示
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x, y)
ax.grid()
# ===================================== 散布図に回帰直線を上書き
xmin = x.min()
xmax = x.max()
ax.plot([xmin,xmax],[a+b*xmin,a+b*xmax], color='r', linewidth=4)
# ================= 散布図に相関係数を上書き
text = 'r = ' + str(round(r,2))
ax.text(170,35, text, size=14)
fig.show()
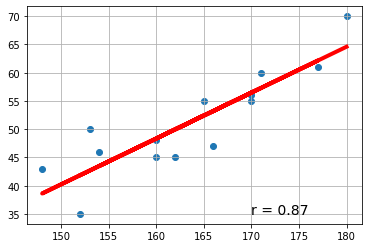
線形回帰の分野では、scikit-learn (sklearn)拡張ライブラリを用いると、簡潔に多様な情報が得られます。
これを用いるには、次の宣言をします。
from sklearn import linear_model
slr = linear_model.LinearRegression()
sklearnでは、y = a0 + a1.x1 + a2.x2 + … のような多変数回帰を対象にしています。それで、入力データは、説明関数(y)は1次元ベクトル(行ベクトルでも列ベクトルでもよい)、説明変数(x)は二次元の列ベクトルになります。
x の入力記述を簡素化するために、右の xt のようにしたいときがあります。そのときは x = xt.T として転置します。
x1 x2
y = [100, 200, 300] x = [ [10, 11] xt = [ [10, 20, 30] x1
[20, 21] [11, 21, 31] ] x2
[30, 31] ]
import numpy as np
import matplotlib.pyplot as plt
# scikit-learnの利用宣言
from sklearn import linear_model
slr = linear_model.LinearRegression()
# ========================入力データ
y = np.array([ 70, 55, 45, 60, 45, 55, 43, 50, 56, 46, 48, 47, 61, 35])
xt = np.array([[180,170,162,171,160,165,148,153,170,154,160,166,177,152]])
# sklearnでは、
x = xt.T # 転置行列
# array([[180],
# [170],
# ;
# [152]])
# ======================== 回帰の計算
slr.fit(x, y) # これだけで回帰式や相関係数などが計算できます。
# 得られる諸元 説明は冗長になるので、この通りで取り出せると理解する
b = slr.coef_[0] # 切片 slr.coef_ が [0.812] なのでスカラーにする
a = slr.intercept_ # x の係数
r2 = slr.score(x, y) # 決定係数 相関係数の2乗
r = np.sqrt(r2) # 相関係数
print('a (切片, slr.intercept_) = ',a, ' + b (回帰係数. slr.coef_) = ', b, '*x')
# a (切片, slr.intercept_) = -81.56 + b (回帰係数. slr.coef_) = 0.81*x
print('r2 (決定係数, slr.score(x, y) ) = ', r2, ', r (信頼係数 r = sqrt(r2) ) = ', r)
# r2 (決定係数, slr.score(x, y) ) = 0.76, r (信頼係数 r = sqrt(r2) ) = 0.87
# ======================== 散布図の作成
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x, y) # xはxiでもよい
ax.grid()
# ============= 回帰直線の追加
ax.plot(x, slr.predict(x), color='r', linewidth=4)
# slr.predict(x):x における回帰直線のyの値を戻す
# x の各点での y = a + bx を計算し、各点 (x0,y0),(x1,y1),(x2,y2), をつないだ線になる
# ================= 散布図に相関係数を上書き
text = 'r = ' + str(round(r,2))
ax.text(170,35, text, size=14)
fig.show()
a (切片, slr.intercept_) = -81.555 + b (回帰係数. slr.coef_) = 0.8119 *x
r2 (決定係数, slr.score(x, y) ) = 0.7616, r (信頼係数 r = sqrt(r2) ) = 0.8727
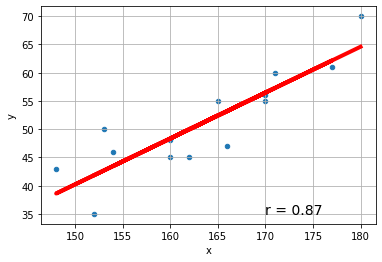
sklearnでの関数が列ベクトル形の行列を想定していることは、入力データを DataFrame(df) で与えることを前提としているように思われます。
しかし、内部処理ではほとんどが数値計算になるので、ndarray に変換することになります。
import numpy as np
import pandas as pd # Pandasの利用宣言
import matplotlib.pyplot as plt
from sklearn import linear_model
slr = linear_model.LinearRegression()
# ========================入力データ
df = pd.DataFrame([[180, 70], [170, 55], [162, 45], [171, 60], [160, 45],
[165, 55], [148, 43], [153, 50], [170, 56], [154, 46],
[160, 48], [166, 47], [177, 61], [152, 35]],
columns = ['x', 'y'])
x = df[['x']].values # 列ベクトルにする
y = df['y'].values # 行ベクトルでよい
# ======================== 回帰の計算
slr.fit(x, y)
# ============= 得られた諸元
b = slr.coef_[0] # slr.coef_ が [0.812] なのでスカラーにする
a = slr.intercept_
r2 = slr.score(x, y)
r = np.sqrt(r2)
print('a (切片, slr.intercept_) = ',a, ' + b (回帰係数. slr.coef_) = ', b, '*x')
# a (切片, slr.intercept_) = -81.56 + b (回帰係数. slr.coef_) = 0.81*x
print('r2 (決定係数, slr.score(x, y) ) = ', r2, ', r (信頼係数 r = sqrt(r2) ) = ', r)
# r2 (決定係数, slr.score(x, y) ) = 0.76, r (信頼係数 r = sqrt(r2) ) = 0.87
# ======================== 散布図の作成 df.plotによる記述もできます
fig = plt.figure()
ax = df.plot(x='x', y='y', kind = 'scatter', grid=True)
# ============= 回帰直線の追加
ax.plot(x, slr.predict(x), color='r', linewidth=4)
# ================= 散布図に相関係数を上書き
text = 'r = ' + str(round(r,2))
ax.text(170,35, text, size=14)
fig.show()
a (切片, slr.intercept_) = -81.555 + b (回帰係数. slr.coef_) = 0.8119 *x
r2 (決定係数, slr.score(x, y) ) = 0.7616, r (信頼係数 r = sqrt(r2) ) = 0.8727
import numpy as np
import matplotlib.pyplot as plt
# scikit-learnの利用宣言
from sklearn import linear_model
slr = linear_model.LinearRegression()
# ========================入力データ
y = np.array([ 70, 55, 45, 60, 45, 55, 43, 50, 56, 46, 48, 47, 61, 35])
xt = np.array([[180,170,162,171,160,165,148,153,170,154,160,166,177,152]])
x = xt.T
# ======================== 回帰の計算
slr.fit(x, y)
# ============= 得られた諸元
b = slr.coef_[0]
a = slr.intercept_
r2 = slr.score(x, y)
r = np.sqrt(r2)
if b < 0:
r = -r
print('a (切片, slr.intercept_) = ',a, ' + b (回帰係数. slr.coef_) = ', b, '*x')
# a (切片, slr.intercept_) = -81.56 + b (回帰係数. slr.coef_) = 0.81*x
print('r2 (決定係数, slr.score(x, y) ) = ', r2, ', r (信頼係数 r = sqrt(r2) ) = ', r)
# r2 (決定係数, slr.score(x, y) ) = 0.76, r (信頼係数 r = sqrt(r2) ) = 0.87
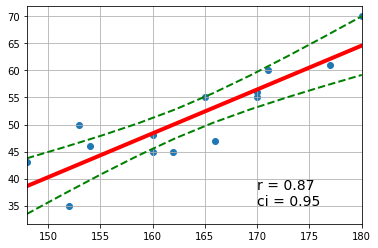
# ====================================== ここからが追加部分
p2 = 0.95 # 信頼確率 95% (信頼区間の計算に用いる)
# ======================== 基本統計量の計算
n = len(x) # 組数:n= 14
xmin = x.min() # x の最小値
xmax = x.max() # x の最大値
mx = x.mean() # 平均:mx=163.4
sdx = x.std() # x の標準偏差
# ======================== t分布の値とscipyライブラリ
from scipy import stats # t.ppt(α,自由度) を使うために必要
p = (1+p2)/2 # p2=0.95は「入力データ」で指定、片側確率 (1+0.95)/2=0.975
t = stats.t.ppf(p, n-2) # t(0.975,12)=2.179
print('t(',p, ', ', n-2, ') = ',t)
# ================= 誤差の統計量
yr = a + b*x # 各xに対応する回帰直線のyの値(xが列ベクトルなので)
yr = yr[:,0] # 列ベクトルを行ベクトルに変換
ye = y - yr # 誤差
see = np.sum(ye**2) # 誤差平方和 248.308
sde = np.sqrt(see/(n-2)) # 誤差標準偏差 4.548
# ================= x,y の付けなおし
u = np.linspace(xmin, xmax, 10) # 新規に等間隔のxの値
v = a + b*u # uに対応する回帰直線の値
# ================= 信頼区間の計算
ci = t*sde/np.sqrt(n)*np.sqrt(1+((u-mx)/sdx)**2) # 信頼区間幅
upper = v + np.abs(ci)
lower = v - np.abs(ci)
# ======================== 散布図等の作成
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.set_xlim(xmin, xmax) # グラフの表示範囲
ax.scatter(x, y) # 散布図
ax.plot(u, v, 'r-', linewidth=4) # 回帰直線
ax.plot(u, upper, 'g--', linewidth=2) # 上側信頼範囲
ax.plot(u, lower, 'g--', linewidth=2) # 下側信頼範囲
ax.grid()
text = ('r = ' + str(round(r,2)) + '\nci = ' + str(p2))
ax.text(170, 35, text, size=14)
a (切片, slr.intercept_) = -81.555 + b (回帰係数. slr.coef_) = 0.8119 *x
r2 (決定係数, slr.score(x, y) ) = 0.7616, r (信頼係数 r = sqrt(r2) ) = 0.8727
t( 0.975,12 ) = 2.17 ci = 0.95
複数の説明変数がある場合です。回帰直線は、
y = a + b[0]x0 + b[1]x1 + …
になります。
説明変数間の値が大きく違うと、正確な処理ができので、各変数を、平均0、標準偏差1に変換、0~1の範囲に変換などの正規化をすべきです。
しかし煩雑になりますので、ここでは正規化の操作はしていません。
X軸が複数の変数になるため、散布図は作れません。ここでは、a, b の値を求めるだけにします。 その数学的な説明は、「重相関と重回帰」を参照
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
slr = linear_model.LinearRegression()
# ========================入力データ
xi = np.array([[180,170,162,171,160,165,148,153,170,154,160,166,177,152],
[ 86, 84, 85, 84, 83, 82, 74, 81, 82, 82, 76, 75, 83, 77]])
y = np.array( [ 70, 55, 45, 60, 45, 55, 43, 50, 56, 46, 48, 47, 61, 35])
x = xi.T
# ======================== 基本統計量
m = len(x[0]) # xの系列数 2
n = len(y) # 要素数 14
ymean = y.mean() # y の平均 51.14
# ======================== 回帰の計算
slr.fit(x, y)
# ============= 回帰直線の式
b = slr.coef_ # 偏回帰係数(回帰直線の係数) [0.7291 0.341]
print('b = ',b)
a = slr.intercept_ # _回帰直線の定数項 -95.541
print('y = ',a,' + ',b[0],'*x[0] + ',b[1],'*x[1] + ...')
# y = -95.541 + 0.7291*x[0] + 0.341*x[1]
# ============= 決定係数
yr = slr.predict(x)
ye = y - yr
sall = ((y - ymean)**2).sum() # 全変動 1041.71
sreg = ((yr - ymean)**2).sum() # 回帰変動 807.80
sres = sall - sreg # 残差変動 233.91
r2 = 1-(sres/(n-1-m))/(sall/(n-1)) # 決定係数 0.7346
r = np.sqrt(r2) # 相関係数 0.857
# ============= 相関行列
corr = np.corrcoef(x.T) # T は転置行列 ┌ x[0]とx[1]の相関
print('corr\n',corr) # array([[1. , 0.605],
# [0.605, 1.])
b = [0.7287 0.3405]
y = -95.5414 + 0.7287*x[0] + 0.3405*x[1]
corr
[[1 0.6053]
[0.6053 1. ]]
単純な統計量を得るだけなら、Pandas の DataFrame(df)を対象にした関数を使うのが簡便です。
import numpy as np
import pandas as pd
df = pd.DataFrame([
[3, 4, 4, 5, 4, 4],
[6, 6, 7, 8, 7, 7],
[6, 5, 7, 5, 5, 6],
[6, 7, 5, 4, 6, 5],
[5, 7, 6, 5, 5, 5],
[4, 5, 5, 5, 6, 6],
[6, 6, 7, 6, 4, 4],
[5, 5, 4, 5, 5, 6],
[6, 6, 6, 7, 7, 6],
[6, 5, 6, 6, 5, 5],
[5, 4, 4, 5, 5, 5],
[5, 5, 6, 5, 4, 5],
[6, 6, 5, 5, 6, 5],
[5, 5, 4, 4, 5, 3],
[5, 6, 4, 5, 6, 6],
[6, 6, 6, 4, 4, 5],
[4, 4, 3, 6, 5, 6],
[6, 6, 7, 4, 5, 5],
[5, 3, 4, 3, 5, 4],
[4, 6, 6, 3, 5, 4]],
columns = ['c0','c1','c2','c3','c4','c5'])
# ============= 基本統計量
print('df.describe()\n',df.describe())
df.describe()
# c0 c1 c2 c3 c4 c5
# count 20. 20. 20. 20. 20. 20.
# mean 5.2 5.35 5.3 5. 5.2 5.1
# std 0.89 1.04 1.26 1.21 0.894 0.97
# min 3. 3. 3. 3. 4. 3.
# 25% 5. 5. 4. 4. 5. 4.75
# 50% 5. 5.5 5.5 5. 5. 5.
# 75% 6. 6. 6 5.25 6 6.
# max 6. 7. 7. 8. 7. 7.
# ============= 相関係数
df.corr()
# c0 c1 c2 c3 c4 c5
# c0 1. 0.486 0.597 0.242 0.276 0.218
# c1 0.486 1. 0.557 0.125 0.316 0.172
# c2 0.597 0.557 1. 0.240 0.037 0.146
# c3 0.242 0.125 0.240 1. 0.436 0.627
# c4 0.276 0.316 0.037 0.436 1. 0.583
# c5 0.218 0.172 0.146 0.627 0.583 1.