分布に従う乱数の発生

一様分布

●連続
function xRandomUni(xmin, xmax) {
　　return xmin + (xmax - xmin)*Math.random();　　　・・・Ａ
}

一様分布は、左図のようにxmin～xmaxの区間での発生確率が等しい（一様）な分布です。Math.random()は０～１の一様分布に従う乱数ですから、０→xmin、１→xmaxに広げる操作をします。右図のようになりますので、Ａの式になります。

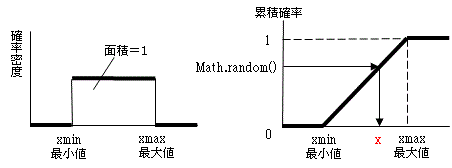
　ここでは、表作成の都合から、7.5～8.5なら８とする（四捨五入する）ことにして表示しています。１０等分したので、通常の区間では確率は1/10=0.1になり、両端（５と１５）はその半分になっています。

（ここでは10,000回も行ったので、キレイな形になりましたが、回数が少ないと偶然により、乱れた形になります。回数を100, 200, 500, 1000と変えて確認してください。このように、シミュレーションで信頼性を高めるには、多数回にする必要があります。）

●整数
function iRandomUni(imin, imax) {
　　return imin + Math.floor( (imax - imin + 1)*Math.random() );　・・・Ｂ
}

求める値が人数だというような場合、整数であることが重要な場合もあります。
　整数にするには、Ｂの式を用います。上述のように四捨五入するのでは、両端の値が半分になってしまいます。両端の左右に０.５広げて（１を加える）必要があります。連続のときは１０等分したのに、整数のときは５と１５を含む１１等分するので、各点の確率は0.1よりも少なくなります。

三角分布

三角分布とは、左図のように３点を与えた三角形の確率密度になる分布です。

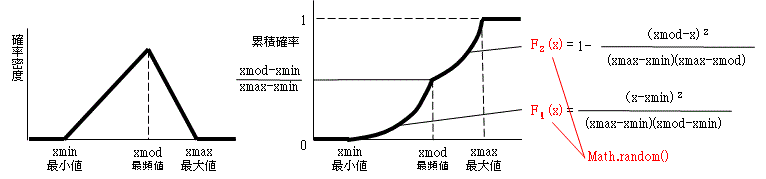
　費用や期間などを想定するとき、楽観値（xmin）と悲観値（xmin）以外に、最もありそうな値として最頻値（xmod）を想定することがよくあります。そのため、シミュレーションモデルでは、三角分布に従う乱数が使われる機会が多いのです。

三角分布の累積確率は右図のように、最頻値の左側と右側で異なる式になります。ここでＦ(x)がMath.randam()で与えられるので、 その値により、用いる式を決定し、式を変形してｘを求めればよいのです。

しかし、これは煩雑です。ここで「２つの０～１の一様乱数ｕとvの差は、最小値０、最大値１、最頻値１／２の三角分布に従う」という理論があります。
　それに最頻値０≦ｃ≦１を加味することにより、０～１の三角分布の乱数x01は、
　　　x01 = (1-c)*(ｕ，ｖの小さいほう) + c*(ｕ，ｖの小さいほう)　・・・Ａ
となります。それをxmin～xmaxに広げれば（Ｂ）よいのです。
　実際に、多数の組で実験すると、三角分布になっていることがわかります。

function xRandomTri(xmin, xmax, xmod) {
　　var c = (xmod-xmin)/(xmax-xmin);
　　var u = Math.random();
　　var v = Math.random();
　　if (u > v) var x01 = (1-c)*v + c*u;　　　┬─　Ａ
　　else　　　　　x01 = (1-c)*u + c*v; 　　　┘
　　return xmin + (xmax - xmin)*x01;　　　・・・　Ｂ
}

正規分布

function xRandomNormal(average, deviation) {
　　var z01 = 0;
　　for (var i=1; i<=12; i++) { 　　　┐
　　　　z01 = z01 + Math.random();　　├─　Ａ
　　} 　　　　　　　　　　　　　　　　│
　　z01 = z01 - 6;　　　　　　　　　　┘
　　return (average + z01) + (deviation * z01);　・・・Ｂ
}

一様分布に従う０～１の乱数は，平均 μ ＝ 1／2 ，分散 σ² ＝ 1／12 です。中心極限定理より、この一様乱数１２個の合計値の分布は、μ ＝ 6 ，σ²＝ 1 の正規分布に近似できます。σ²＝ 1 より、標準偏差σ＝１になります。すなわち、
　　「１２個のMath.random()の合計－６」は「平均０、標準偏差１」の分布になる　→Ａのz01
になります。
　これに与件の平均（average）と標準偏差（deviation）を加味する（Ｂ）と、平均＝average、標準偏差＝deviationの正規分布乱数になります。→参照：「正規分布」

整数化するとき、両端の確率は非常に小さい値になるので、連続で得たＢの値を単純に四捨五入すればよいのです。
function iRandomNormal(average, deviation) {
　　var z01 = 0;
　　for (var i=1; i<=12; i++) {
　　　　z01 =z01 + Math.random();
　　}
　　z01 = z01 - 6;
　　return Math.round(average + z01 + deviation*z01)　　　・・・Ｃ;
}

正規分布（上下限）

シミュレーションなどを行うとき、あまりにも小さい（大きい）値があると、極端な結果になることがあります。また、例えば男性成人の身長が正規分布になるといっても、１ｍ未満や２.５ｍ以上の人がいるとは考えにくいでしょう。それで実務的には、最小値～最大値を設けるのが一般的です。
　求める方法は単純で、範囲内の値になる（Ｄ）まで、繰り返し通常の正規分布の計算をさせるだけです。

function xRandomNormalMinmax(xmin, xmax, average, deviation) {
　　var ok = 0;　　　 // 範囲内なら１、範囲外なら０
　　while (ok==0) {
　　　　var z01 = 0;　　　　　　　　　　　　　　　　　　┐
　　　　for (var i=1; i<=12; i++) {　　 　　　　　　　　│
　　　　　　z01 =z01 + Math.random(); 　　　　　　　　　├─（通常の）
　　　　} 　　　　　　　　　　　　　　　　　　　　　　　│　　正規分布
　　　　z01 = z01 - 6;　　　　　　　　　　　　　　　　　│
　　　　var x =　(average + z01) + (deviation * z01); 　┘
　　　　if ( (x >= xmin) && (x <= xmax) ) ok = 1;　・・・Ｄ
　　}
　　return x;　　　　　　　　　　　　　　　　　　　・・・Ｅ
}

整数の場合も同様ですが、「範囲内」の指定が両端を0.5広げ（Ｄ'）て、結果のｘを四捨五入します（Ｅ'）
function iRandomNormalMinmax(imin, imax, average, deviation) {
　　var ok = 0;
　　while (ok==0) {
　　　　var z01 = 0;
　　　　for (var i=1; i<=12; i++) {
　　　　　　z01 =z01 + Math.random();
　　　　}
　　　　z01 = z01 - 6;
　　　　var x =　(average + z01) + (deviation * z01);
　　　　if ( (x >= imin-0.499) && (x <= imax+0.499) ) ok = 1;　・・・Ｄ'
　　}
　　return Math.round(x);　　　　　　　　　　　　　　　　　　　・・・Ｅ'
}

指数分布

単位時間中にある事象が発生するのは、他の事象に関係なく独立だとすれば、単位時間中に事象が発生する平均回数をλとするとき、その事象の発生間隔がｔ単位時間である確率密度Ｐ(ｔ)は、
　　　Ｐ(t)＝λｅ^－λｔ
の指数分布に従います。
　そして、０～ｔの累積確率は、
　　　Ｐ(≦ｔ)＝１－ｅ^－λｔ
になります。→参照：「ポアソン分布と指数分布」
　ここでＰ(≦ｔ)＝Math.random()として変形すると
　　　ｔ = (－１／λ)log_e(1- Math.random())
となります。
　このｔが、平均λの指数分布に従う乱数になります。
function xRandomExp(lambda) {
　　return -1/lambda*Math.log(1- Math.random());
}

指数乱数は、「待ち行列」のシミュレーションによく用いられます。
　事象発生の平均回数がλ[回/時間]とは、ある事象が発生してから次の事象が発生するまでの平均間隔時間が１／λ[時間]だということです。例えば、客が来てから次の客が来るまでの間隔が平均５分だとすれば、λ＝１／５になります。ここで得られた値ｘが、ある客が到着してから、次の客が到着するまでの間隔時間になります。

整数化するための定式化は私には理論的な説明ができません。それでやや強引な方法を採りました。
　平均到着間隔（１／λ）を０.５だけ大きくして計算し（Ａ）、結果を四捨五入する（Ｂ）ことにしました。
　　　１／λ'＝１／λ＋0.5　　　　∴λ'=λ/(１＋0.5λ
function iRandomExp(lambda) {
　　var lambda1 = lambda/(1+0.5*lambda);　　　　　　　　　　　　　・・・Ａ
　　return Math.round( -1/lambda1*Math.log(1- Math.random()) ); 　・・・Ｂ
}

指数分布（上下限）

指数分布の結果は（名称のように）０近辺（同時に客がくる）が多くなり、裾野が長い（次の客がなかなか来ない）のが特徴です。そのため、現実とは異なるシミュレーション結果になるので、範囲を与えることがあります。
　その調整方法として、範囲内の値になるまで、通常の（範囲指定のない）指数分布の計算を繰り返すことにしました。

連続
function xRandomExpMinmax(xmin, xmax, lambda) {
　　var ok = 0;
　　while　(ok==0) {　　　　　　　　　　　　　　　　　　　┐
　　　　var x = -1/lambda*Math.log(1- Math.random());　　├─（通常の）
　　　　if ( (x>=xmin) && (x<=xmax) ) ok = 1; 　　　　　　│　　指数分布
　　}　　　　　　　　　　　　　　　　　　　　　　　　　　　┘
　　return x;
}

整数のときも同様に、指数分布（整数）を繰り返します。

function iRandomExpMinmax(imin, imax, lambda) {
　　var lambda1 = lambda/(1+0.5*lambda);
　　var ok = 0;
　　while　(ok==0) { 　　　　　　　　　　　　　　　　　　　┐
　　　　var x = -1/lambda1*Math.log(1- Math.random());　　├─（通常の）
　　　　if ( (x>=imin-0.499) && (x<=imax+0.499) ) ok = 1; │　　指数分布
　　} 　　　　　　　　　　　　　　　　　　　　　　　　　　　┘
　　return Math.round(x);
}