スタートページ＞ JavaScript＞ ライブラリ目次

乱数発生関連 JavaScript関数ライブラリ rand.js の利用解説書

ご利用にあたって

一般事項

分布に従う乱数の生成の一般的方法（左図）

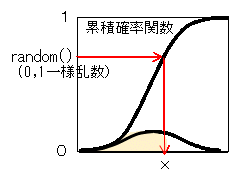
JavaScriptでの乱数発生関数には、０～１の一様分布を対象にした random() があるだけです。
random() を用いて正規分布や指数分布などに従う乱数を発生する関数を作成します。
その基本的な方法は、累積確率関数の逆関数（参照：確率統計分布）を用いる方法です。
累積確率関数は左図のように０～１の値をとるので、random() の値からｘを求める逆関数により、分布に従う乱数が生成できます。
分布によっては、この逆関数が複雑な構造になる場合もあり、いろいろな代替手段が開発されています。

範囲指定の乱数（右図）

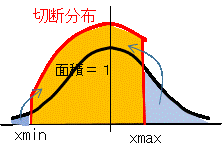
実務では、例えば成績の分布など正規分布に従うが、その範囲は０～１００に限定されるときがあります。
また、シミュレーションを行うとき、あまりにも極端な値の乱数が出現すると、現実的ではない状況になります。
それを防ぐには右図のような切断分布に変形する必要があります。
ところが、元の平均や分散などの特性値を保持しながら切断分布に変形するには非常に複雑な計算になります。
そのため、ここでは例外を除き取り扱いません。

［実行］について

ここでは、プログラムの説明のトレースではなく、ｎ個の乱数を発生させたときの理論値との差異を出力しています。
そのとき、表作成の都合により連続量を整数値で代表させているので、不正確（特に両端で）な場合があります。

一様分布乱数
　　連続： x = randUni(xmin, xmax); 　
　　整数： i = randUniInt(imin, imax); 　

下の表では、連続のときは、得たｘを四捨五入して表示しているので、最小値と最大値の割合は他の半分になっています。
整数のときは、区間を xmin～xmin+1として、乱数を発生させ、得たｘを切り捨てているので、同じ値になっています。

最小値= 最大値= n=

　　

正規分布乱数
　　x = randNormal([μ, σ]) 　
　　x = randNormal12([μ, σ]) 　
　　x = randNormal2([μ, σ]) 　

μ, σを省略（一方だけの省略は不可）したとき、μ＝０, σ＝１になります。
randNormal
　正規分布の累積確率の逆関数を用います。
randNormal12
　中心極限定理により、多数の一様分布に従う標本の和は正規分布になります。
　Math.random()を１２個を合計した値は、μ＝６、σ＝１の正規分布に近づきます。
randNormal2
  二つのMath.random() を r1, r2 とすると、
 　　z1 = √(-2*log(r1)) * sin(2π*r2)
 　　z2 = √(-2*log(r2)) * cos(2π*r1)　
  はμ＝０, σ＝１の正規分布乱数になります。ここでは z1 を用いました。　
μ= σ= n=

三角分布
　　x = randTri(xmin, xmax, xmod); 　

xmodは最頻値、平均は (xmin+xmax+xmod)/3 になる。
三角分布の累積確率の逆関数を利用してもよいが、二つの一様分布乱数、u, v (u>vとする）として、
　　　(1-c)*v + c*u　　　　c = (xmod-xmin)/(xmax-xmin)
とすることにより、xmin=0, xmax=1, xmod=c の三角分布乱数が得られる。
xmin＝ xmax＝ xmod＝ n＝

指数分布
　　　x = randExp(λ); 　
　　　x = randExpMax(λ, xmax); 　

単位時間中にある事象が発生する平均回数をλとするとき、その事象の発生間隔がx単位時間である確率は指数分布に従う。
  累積確率 F(x) = 1-e-λx
　累積確率の逆関数は、x = -(1/λ)*log(1-random())
  参照：「ポアソン分布と指数分布」

randExpMax(λ, xmax) は切断指数分布
  指数分布は裾が長いので、極端な値にならないよう上限を与えることがある。乱数は０～xmaxになる。
  F(xmax) = (1-e-λx)/(1-e-λxmax)
  この逆関数は　x =  -(1/λ)*log(1-(1-e-λxmax)*random()) となる
　　　
「理論値」とは、点ｘにおける確率密度の値。
連続量を整数値で代表させるため、結果を単純に四捨五入している。
  x=0 では0～0.5で幅が狭いので、小さめになる傾向がある。そのため最頻値が０のときに１となることが多い。
λ＝ xmax= n＝

ポアソン分布
　　　x = randPoisson(λ); 　

平均発生確率がλであるとき、ｘ回発生する確率を求めます。ｘは１以上の整数になります。
指数関数と対数関数の関係（詳細省略）から
　　ｅ-λ ≧ Π(rondom())　　k=0,1,…,x
が成立する最小の x がポアソン分布乱数になります。乱数は整数値です。
λ＝ n＝