問題の理解
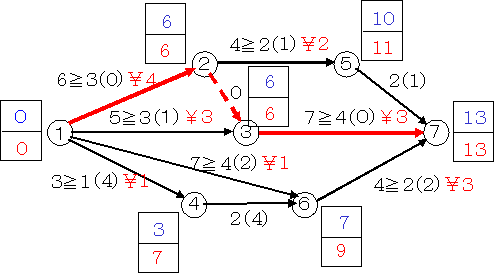
下のアローダイヤグラムで赤線がクリティカル・パスを示しており,このプロジェクトの最短完了時刻は27日です。
ここで,人員増強や機械の利用などにより追加費用をかければ所用時間を短縮できるとします。例えば作業1-2は所要時間は6日ですが,1日あたり5円/日(これを費用勾配といいます)の費用を追加することにより,特急時間4日にまで短縮できるとします。これを下のアローダイヤグラムでは
所要時間≧(余裕時間)¥費用勾配
の形式で表示しました。なお,費用をかけても短縮できない作業は,特急時間と費用勾配を省略しています。
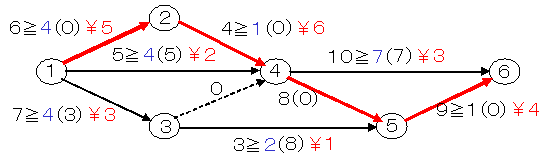
全体所要日数=27日
クリティカルパス=1→2→4→5→6
開始 終了 日数 特急日数 費用勾配 (余裕)
1 2 6 4 5 0
1 3 7 4 3 3
1 4 5 4 2 5
2 4 4 1 6 0
3 4 0 0 ∞ 0
3 5 3 2 1 8
4 5 8 0 ∞ 0
5 6 9 1 4 0
この最短完了時刻27日を26日,25日,・・・というように短縮したいのですが,追加費用を最小限にして短縮するには,どの作業を短縮すればよいかというのが問題です。このような問題の解法にはCPM(クリティカル・パス・メソッド)という手法があります。
短縮の手順
短縮1
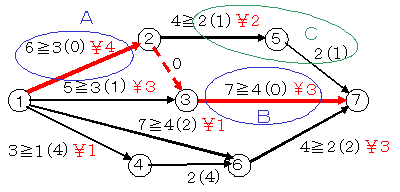
クリティカル・パスの作業のうちから費用勾配の小さい作業を短縮することになります。全作業での費用勾配が最小のものは作業3-5の1円ですが,これはクリティカル・パスの作業ではないので,この作業を短縮してもプロジェクトの短縮にはなりません。クリティカル・パスのなかでは作業5-6の4円が最小ですから,それを短縮することを考えます。特急時間は1日ですが,この作業が2日になると作業4-5の余裕がなくなりますので,とりあえず2日までに短縮することにします。
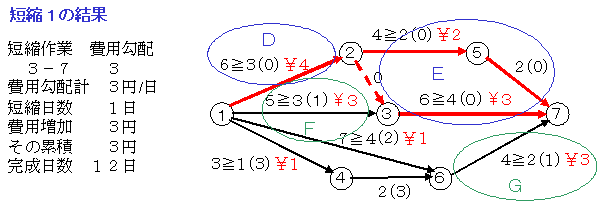
これにより,4円×7日=28円の追加費用がかかりますがプロジェクトは7日短縮されました。なお,作業4-6の余裕時間がなくなりクリティカルな作業になりました。その結果は次のようになります。
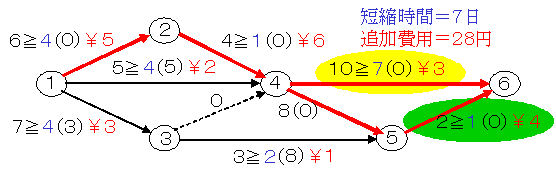
短縮2
作業5-6と作業4-6でさらに1日短縮しようとすると,この2つの作業の費用勾配が3+4=7円になります。それよりもクリティカル・パスでの作業1-2の費用勾配5のほうが安いので,それを特急時間4日まで短縮します。2日短縮され,追加費用は10円です。この短縮をしてもクリティカル・パスには変化がありません。
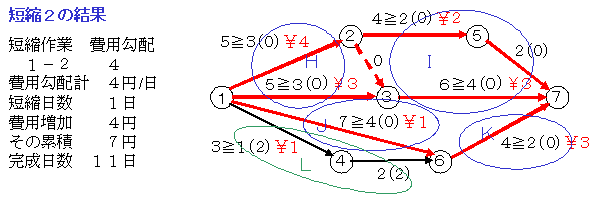
次にクリティカル・パスで費用勾配が小さいのは作業2-4の6円です。ここで1日短縮すると作業1-3がクリティカルになりますので,作業2-4を3日で行うことにします。ここまででアローダイヤグラムは次のようになります。
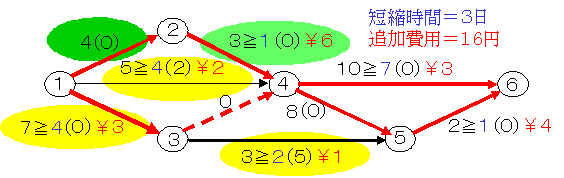
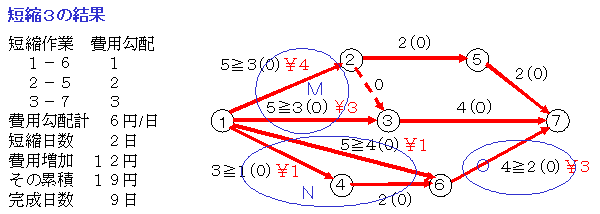
短縮3
イベント4の左右について考えます。イベント4よりも左側で短縮するには,作業1-3と作業2-4を同時に短縮するので,費用勾配は3+6=9円になります。それに対して右側では,作業4-6と作業5-6を同時に短縮するので,費用勾配は3+4=7円ですから,こちらのほうで作業5-6の特急時間限度1日まで短縮します。
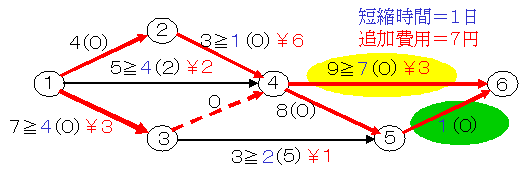
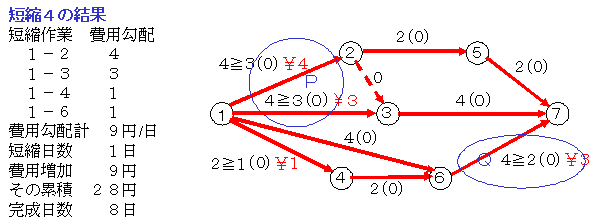
短縮4
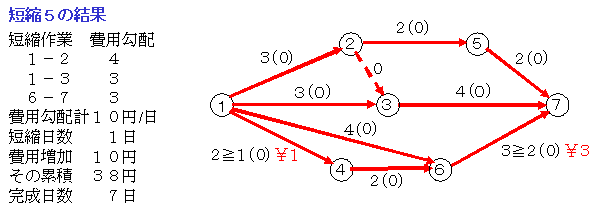
イベント4の右側では,もはや短縮することはできませんので,作業1-3と作業2-4を短縮します。その限界は作業2-4の2日です。その結果,作業1-4もクリティカルになりました。この段階で,作業1-2,2-4,4-5,5-6のクリティカル・パスが短縮不可能になりましたので,これ以上は短縮できないことになります。
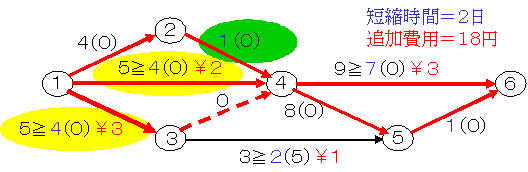
以上の短縮経過を表にすると次のようになります。
短縮作業 費用勾配 短縮時間 追加費用 その累計 完了時刻
5-6 4円/日 7日 28円 28円 20日
1-2 5 2 10 38 18
2-4 6 1 6 44 17
4-6,5-6 7 1 7 51 16
1-3,2-4 9 2 18 69 14