問題の理解
| Aのペイオフ ・マトリクス |
Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | 1 | -3 |
| A2 | -2 | 4 | |
右のペイオフ・マトリクスは,AにはA1とA2の戦略があり,BにはB1とB2の戦略があり,AがA1を選択してBがB1を選択したとき,Aには1の利益がありBには1の損失があることを示しています。すなわち,これはAから見た利失を表しています。
Aは,このペイオフ・マトリクスにより利益が最大になるようにA1・A2の戦略を選択し,BはAの利益が最小になるようにB1・B2の戦略を選択します。このような敵対関係にあるときの戦略選択の方法を考える手法がゲームの理論です。
ゲームの理論では,互いに相手が論理的な戦略を採ることを前提にしています。もし,Bがペイオフ・マトリクスを知っているのに,最善の戦略(すなわちAの利益を最小にする手)を採らないこともあるとすると,以下の論理は存在しないことになります。
ゲームの理論のうち,最も単純なのが,この例のように関係者がAとBの2人だけで,Aの利益はBの損失であり2人の利失の合計は0である場合です。それを2人零和ゲームといいます。
優越戦略と劣等戦略
| ケース1 | Bの戦略 | B1 | B2 | B3 | B4 |
|---|---|---|---|---|---|
| Aの戦略 | A1 | 1 | -2 | -1 | 2 |
| A2 | -2 | 4 | 5 | 0 | |
| A3 | -3 | 2 | 2 | -1 | |
| ケース2 | Bの戦略 | B1 | B2 | B3 | B4 |
|---|---|---|---|---|---|
| Aの戦略 | A1 | 1 | -2 | -1 | 2 |
| A2 | -2 | 4 | 5 | 0 | |
| ケース3 | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | 1 | -3 |
| A2 | -2 | 4 | |
ケース1のペイオフ・マトリクスがあるとします。A3の各要素はA2の各要素よりも劣っています。このような関係があるとき,A2はA3に対して優越戦略であり,A3はA2に対して劣等戦略であるといいます。Aは絶対にA3を選択することはありませんから,A3の行は削除しますと,ケース2になります。
すると,Bから見たときには,B3はB2に対して劣等戦略でありB4はB1に対して劣等戦略です。BがB3やB4を選択するはずがありません。それでこれらを削除します。その結果,ケース3になりますが,これらには優越・劣等の関係はないので,これ以上削除する行や列はありません。
鞍点がある場合-純粋戦略
| 鞍点あり | Bの戦略 | 最小値 | B1 | B2 | B3 |
|---|---|---|---|---|---|
| Aの戦略 | A1 | 3 | -1 | -2 | -2 |
| A2 | -1 | 0 | 4 | -1 | |
| A3 | 2 | 1 | 2 | 1 | |
| 最大値 | 3 | 1 | 2 | ||
右のペイオフ・マトリクスのケースを考えます。たまたまAがA3を選択すると,BはA3の行のうちの最小の1にさせようとしてB2を選択します。するとAはB2の列での最大の1を得るためにA3を選択します。結局はAはA3,BはB2を選択することで落ち着きます。(A3,B2)の値1は,AとBが適切な行動をしたとき,Aが少なくとも確保できる利益であるともいえます。その値のゲームの解といいます。
「少なくとも確保できる利益」とは,ミニマックス原理の概念でもあります。Aがミニマックス原理で行動すれば,各行の最小値のうち最大のものを選ぶので3を選択します。Bもミニマックス原理で行動すれば,ペイオフ・マトリックスの値の符号が逆転するのですから,各列の最大値のうち最小のものを選ぶのでB2を選択します。
(A3,B2)のような点を鞍点(あんてん)といいます。鞍点は「その行の最小値であり,かつ,列の最大値である点」です。そのような点があるとき,「鞍点を持つ」といいます(鞍点という名称は馬具の鞍の形が横からみれば凹型の曲線,前から見れば凸型の曲線ですが,凹型曲線の最小値であり凸型曲線の最大値である点があることからつけられたものです)。また,鞍点が存在するときには,両者が唯一の戦略を選択しますが,それを純粋戦略といいます。
以上のことを整理すると,「行の最小値であり,かつ,列の最大値である点が存在するとき,その点を鞍点という。両者はその鞍点を持つ戦略を選択するが,それを純粋戦略という。ゲームの値は鞍点の値になる。」といえます。
鞍点がない場合-混合戦略
| 鞍点なし | Bの戦略 | 最小値 | B1 | B2 |
|---|---|---|---|---|
| Aの戦略 | A1 | 1 | -3 | -3 |
| A2 | -2 | 4 | -2 | |
| 最大値 | 1 | 4 | ||
右のペイオフ・マトリクスでは鞍点がありませんので,純粋戦略にはなりません。
AがA1を選択する確率をp,BがB1を選択する確率をqとすると,
(A1,B1)での期待値: 1pq
(A1,B2)での期待値: -3p(1-q)
(A1,B1)での期待値: -2(1-p)q
(A1,B1)での期待値: 4(1-p)(1-q)
ですから,全体でのゲームの値Vは,
V=1pq-3p(1-q)-2(1-p)q+4(1-p)(1-q)
=10pq-7p-6q+4
=10(p-0.6)(q-0.7)-0.2
となります。
ここで,もしAがp=0.8(>0.6)の戦略をとれば,BはVを小さくしたいのですからq=0とするでしょう。またAがp=0.4(<0.6)の戦略をとればBはq=1とするでしょう。そのようなことをさせないために,Aがp=0.6とすれば,Bがqをどのような値にしても,-0.2の値を確保することができます。
逆にBとしては,q-0.7>0とすればAはp=1,q-0.7<0とすればAはp=0にするので,Vは-0.2よりも大になってしまいます。それを防ぐためには,q=0.6とすればよいことになります。
結論として,AはA1を0.6,A2を0.4の確率で選択し,BはB1を0.7,B2を0.3の確率で選択することにより,ゲームの値を-0.2にすることができます。このように,戦略が確率になる場合を混合戦略といいます。
2人零和ゲームと線形計画法
2人零和ゲームは線形計画法(LP:リニア・プログラミング)により解くことができます。線形計画法に関しては別章で取り扱いますので,ここでは説明を省略します。「鞍点なし」のケースを例にします。
BがB1を選択する確率をqとして,ゲームの値をVとすると,AがA1を選択したとき,その期待値は1q-3(1-q)=4p-3ですが,Bはその期待値よりもVの 4p-3≧V 同様にA2を選択したときには,-2q+4(1-q)=-6q+4≧Vとなります。そしてBはVの値を最小にしたいのです。
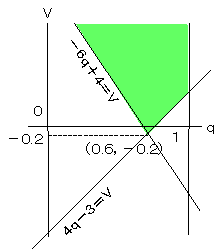 これをまとめると,
これをまとめると,
制約条件
0≦q≦1
4p-3≧V
-6q+4≧V
目的関数
V → 最小
と定式化されます。
これを図式解法により解くと右図から,q=0.7のときVは最小値-0.2となり,前述の結果と同じになります。