データの内部表現（数値・上級）

整数

正整数の１０進、２進、１６進表示と基数変換と関しては、「データの内部表現（数値）」で扱いました。

２数の加算

２進数も１６進数もいったん１０進数に変換して計算し、その結果を元の進数に基数変換すればよいのですが、あえて直接計算することにします。

２進数の加算
　　　　　④③②①
　　　　　　１１０　　　　　　　４×１＋２×１＋１×０　　　　６
　　　＋）　　１１　　　　　　　　　　　２×１＋１×１　　＋）３
　　　　─────　　　　　　　　　　　　　　　　　　　　　──
　　　　　１００１　　　８×１＋４×０＋２×０＋１×１　　　　９

①：０＋１→１
②：１＋１→２になるが２進法では１０→１繰り上がって０→０
③：１と繰り上がりの１→１＋１→１繰り上がって０→０
④：繰り上がりの１→１

１６進数の加算
　　　　　③②①
　　　　　　ＡＢ　　　　　　　　　　１６×１０＋１×１１　　　１７１
　　　＋）　Ｆ２　　　　　　　　　　１６×１５＋１×２　　＋）２４２
　　　　────　　　　　　　　　　　　　　　　　　　　　　────
　　　　　１９Ｄ　　　　２５６×１＋１６×９＋１３　　　　　　４１３

①：Ｂ＋２→１１＋２＝１３→Ｄ
②：Ａ＋Ｆ→１０＋１５＝２５→１６×１＋９→１９→１繰り上がって９→９
③：繰り上がりの１→１

オーバーフロー

「８ビットの２進数」のように、１語のビット数が固定しているときは、次のような計算の結果は９ビットになり、先頭の１は無視されて、結果は００００００００になってします。このような現象をオーバーフローといいます。

　　　　　　　　　　　⑧⑦⑥⑤④③②①
　　　　　　　　　　　１１１１１１１１
　　　　　　　　　＋）０００００００１
　　　　　　　　　　─────────
　　　　　　　　　　１００００００００
　　 オーバーフロー ┘　　　↓
　　　　　　　　　　　００００００００

補数

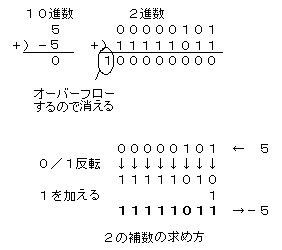
コンピュータでは，演算回路を簡素化するために，加算回路はあるのですが減算回路は持たず，Ａ－Ｂの減算をＡ＋（－Ｂ）として加算にするのです。では，（－Ｂ）をどのように表現するのでしょうか？
　話を簡単にするために，１語を８ビットとします。１０進法の５は２進法では０００００１０１になります。唐突ですがそれに１１１１１０１１を加えると右上図のように結果は０になります。これから，２進数の１１１１１０１１を１０進数の－５であるとすればよいことになります。そのために，８ビット（１語）の先頭ビットが０ならば正数，１ならば負数であるというように決めるのです。このように決めた体系を２の補数表現といいます。０００００１０１の補数は１１１１１０１１であり，１１１１０１１の補数は０００００１０１です。
　補数の求め方は簡単で右下図のように「０／１反転，＋１」の操作を行えばよいのです。
　以下，［１語８ビットで２の補数体系の２進数］の例をいくつか示します。これから，この体系で表現できる値の範囲は，－１２８～０～１２７であることがわかります。
　　　００００００００　　　　　０
　　　０００００００１　　　　　１
　　　０１１１１１１１　　　１２７
　　　１０００００００　　－１２８
　　　１００００００１　　－１２７
　　　１１１１１１１１　　　　－１
練習問題：１バイト２の補数での２進数１１１１０１１１→１０進数？

整数

ここでは説明のため８ビット（１バイト）を１語としていますが、これでは－１２８～１２７の範囲で非現実的です。通常の処理系では３２ビット（４バイト）で２の補数形式の（符号のある）データを整数（int）の１語としています。
　１０進数で１０桁程度になるので、オーバーフローが発生することは稀ですが、巨大な値を扱うときは、long として６４ビットにします。逆に小さなデータしか使わずデータ容量を減らしたいときは short として１６ビットにします。

シフト演算

シフト演算とは、２進数の乗除算を高速にする演算方法です。シフト演算とは、２進数の計算を高速にする演算方法です。
シフト演算には、符号なしデータを対象とする論理シフトと、符号ありデータを対象にする算術シフトがあります。

論理シフト

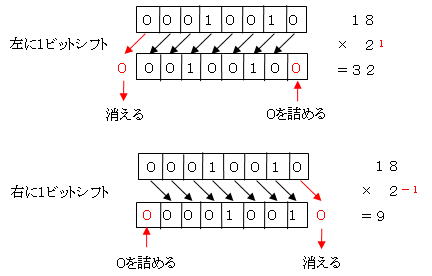
先頭ビットは符号ビットではなく、他のビットと同じ扱いになります。
　例えば、８ビットの２進数
　　　　０００１　００１０　（＝１６＋２＝１８）
を左に１ビットシフトすると（右端には０を詰める）、
　　　　００１０　０１００　（＝３２＋４＝３６）
になります。これは２^１倍したことになります。
　同様に、左に２ビットシフトすれば、２^２＝４倍になります。

右に１ビットシフトすると（左端には０を詰める）、
　　　　００００　１００１　（８＋１＝９）
となり、２^－１＝１／２倍したことになります。

これを組み合わせることにより、
　　「元の数Ａを左に１ビットした数に、Ａを左に２ビットシフトした数を加える」
と、２Ａ＋４Ａ＝６Ａ の計算をしたことになります。

上の２進数を右に４ビットシフトすると、
　　　　０００１　００１０
　　　→００１０　００００
　また、右に２ビットシフトすると
　　　　０００１　００１０
　　　→００００　１０００
となり、赤のビットが消えてしまい、正確な値になりません。
　これをオーバーフロー、アンダーフローといいます。

算術シフト

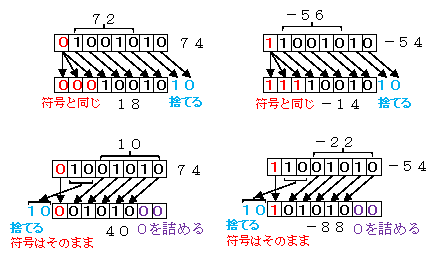
先頭のビットが符号ビットであるデータでのシフト計算です。

●右への２ビット算術シフト（４で割る）上段図
　　符号ビットはそのまま。
　　次の２ビットは符号ビットと同じ。
　　残りのビットは元のビット列から埋めていく。
　　元ビット列であふれたビットは捨てる。
符号ビットが正のとき（左上図）
　　元データ ０１００１０１０ は１０進で７４
　　捨てられるビット１０（＝２）を除外すれば、７４－２＝７２
　　シフト後の０００１００１０は１０進で１８
　　７４／４＝１８の関係になっている。
符号ビットが負のとき（右上図）
　　元データ １１００１０１０ の補数は００１１０１１０＝５４
　　捨てられるビット１０を除外すると５４＋２＝５６
　　シフト後の１１１１００１０の補数は００００１１１０は１０進で１４
　　－５６／４＝－１４
●左への２ビット算術シフト（４倍にする）下段図
左シフトによりオーバーフローが生じるのは論理シフトと同様ですが、算術シフトでは先頭ビットが符号ビットになっているので、実質は７ビットになり、元データの符号ビット直後のシフト分のビット列がオーバーフローすることになります。
　 符号ビットはそのまま。
　　元ビット列の符号ビット直後のシフト分のビット列を捨てる。
　　その後のビット列を結果のビット列に詰める。
　　シフト後の右端の空いた部分を０で詰める。
符号ビットが正のとき（左下図）
　　元ビット列の残った部分は０１０１０＝１０
　　シフト後のビット列は００１０１０００＝４０
　　１０×４＝４０
符号ビットが負のとき（右下図）
　　オーバーフローした部分を１に置き換えると１１１０１０１０となる
　　その補数は０００１０１１０＝２２
　　シフト後の１０１０　１０００の補数は０１０１１０００＝８８
　　－２２×４＝－８８

固定小数点数

固定小数点数とは、１０進数での 12.3 のように小数点をもつデータのことです。２進法では 101.01 のような表記になります。

２進数→１０進数：０.１１０１_２→０.８１２５_１０

右のような表を作成すれば，簡単に計算できます。
練習問題：２進数０.００１１→１０進数？

１０進数→２進数：０.８１２５_１０→０.１１０１_２

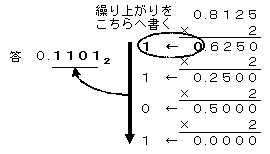１０進数から，０.５（＝１／２），０.２５（＝１／４），０.１２５（＝１／８），・・・，を負にならないように引いていき，０にすることができれば変換できます。

　たとえば０.８１２５は，
　　　０.８１２５＝０.５　　　　（＝１／２　→　０.１_２）
　　　　 　　　　＋０.２５　　　（＝１／４　→　０.０１_２）
　　　　 　　　　＋０.０６３５　（＝１／１６→　０.０００１_２）
ですから，０.１＋０.０１＋０.０００１＝０.１１０１_２となります。

しかし，これよりも次の手順（右図）のほうが簡単でしょう。

1. １０進数を２倍する。整数部分を繰り上がり欄に書き，計算結果の整数部分を０にする。
2. 整数部分を０にした計算結果を新しい１０進数として計算結果が０になるまで，「１」を繰り返す。
3. 計算結果が０になったら，右図のように上から下へ書き下したものが求める２進数である。

練習問題：１０進数０.１８７５→２進数？

〇注意：２進数にできない１０進小数がある！

一般的には，上のように２進数に変換できる１０進小数はむしろ稀なのです。たとえば１０進数の０.１を２進数にしようとすると，
　　　　０.１_１０＝０.０００１１００１１００１１００１１・・・_２
のように循環小数になってしまいます。
　コンピュータでの１語のビット数は有限ですから，どこかで打ち切られてしまいます。これを丸め誤差といいますが，１０進小数をコンピュータで取扱うときには，あくまでも近似値であり正確な値にはならないのです。

１６進数→１０進数：０.０８_１６→１／３２_１０

１６進数の小数点数を１０進数に変換するには、
　　０.１_１６＝１／１６_１０
　　０.０１_１６＝１／１６^２_１０＝１／２５６_１０
　　０.００１_１６＝１／１６^３_１０＝１／４０９６_１０
　　　　：
のように考えます。
　　０.０８_１６＝８×０.０１_１６＝８／２５６_１０＝１／３２_１０

１０進数→１６進数：５／３２_１０→０.２８_１６

分母を１６の累乗とする分数の和に分解します。
５／３２＝　４／３２→２／１６　→２×０.１_１６　→０.２_１６
　　　　　＋１／３２→８／２５６→８×０.０１_１６→０.０８_１６
　　　　＝０.２８_１６

１６進数と２進数の変換

１６進数と２進数の変換は，１０進数をなかがちにして変換することもできますが，２ ^４＝１６であることを利用すると，たとえば
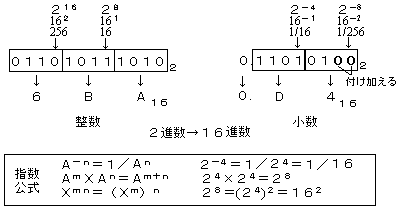　　　１１０１０１１１０１０_２
　　＝１１０_２×２^８＋１０１１_２×２^４＋１０１０_２
　　＝６_１６×１６^２＋Ｂ_１６×１６^１＋Ａ_１６
　　＝６ＢＡ_１６
とすることができます。
　また，小数点以下の数では，
　　　０.１１０１０１_２
　　＝０.１１０１０１００_２
　　＝１１０１_２×２^－４＋０１００_２×２^－８
　　＝Ｄ_１６×１６^－１＋４_１６×１６^－２
　　＝０.Ｄ４_１６
となります。

　すなわち，２進数を１６進数に変換するには，小数点を基準に４個ずつに区切り（右側で４個にならないときは０を入れる），その区切りごとに２進数を１６進数にすればよいことがわかります。逆に，１６進数を２進数に変換するには，１６進数の各数を４桁の２進数にすればよいことになります。
練習問題：１６進数６ＢＡ→８進数？

ＢＣＤコード

ＢＣＤ（Binary Coded Decimal、２進化１０進）コードとは、１バイトを上下の４ビットに区切り、０～９を２進数の４ビットで表すことにより、１バイトで２つの１０進数を表すコードです。

パック１０進数

ＢＣＤコードを用いて任意の桁数の１０進数を表したものです。奇数桁の場合は先頭に０を加え、符号付きの場合は末尾に符号を付けます。
　数値の桁数の大小により、バイト数を指定することができます。１語のバイト数を任意に設定できることを可変長数といいます。整数（２進数）や実数（浮動小数点数）のように１語のバイト数が固定な数を固定長数といいます。
　プログラムで変数を定義するときに、小数点位置を指定することができます。

パック１０進数の特徴は、大きな数を表現できること、除算以外の四則演算で誤差を生じないことです。そのため、取扱金額が大きな会計処理などに向いています。

ゾーン１０進数（アンパックＢＣＤ）

１バイトで１桁の数字を表す数です。文字列でのコード体系とほぼ一致しています。大きな容量になりますが、人による入出力での表現と内部表現が一致していること、コードなど文字列データに計算処理をするときなどに便利です。

これらのデータ型は、汎用コンピュータ上でＣＯＢＯＬ言語やＰＬ／Ｉ言語で記述した事務処理システムでは必須のものでした。ところがほとんどのオープン系言語では通常では対応していません。６４ビット２進数などにしています。また、これらの型への対応も進んでいるようです。

浮動小数点数（実数）

整数型では，取扱える数値が限定されますし，非常に大きな数や小さい数を取扱うことができませんので，科学技術計算などでは困ります。また、通常の科学技術計算では、12.3 というとき、厳密に 12.3000000000 である必要はなく、12.3 に近い数値だということが多いのです。そのような数値を実数といい、実数を表現するには，浮動小数点型を用います。

　　　　　　　　　　整数　　　　　　浮動小数点数
　　　　小数点　　　一般には整数値　小数点あり（実数）
　　　　値の精度　　正確な値　　　　近似値
　　　　大小範囲　　比較的狭い　　　非常に広い
　　　　計算処理　　簡単（高速）　　複雑（低速）　　＊注

例えば、－６４０を－１.２５×２^９ のように、s・f×r^eという形式で表現します。ここで、s（－）を符号、f（１.２５）を仮数，r（２）を基数、ｅ（９）を指数といいます。すなわち、「±仮数×基数^指数」で表現します。基数は、コンピュータ内部では通常は２です（float) が１０を用いる (decimal) こともあります。出力表示の際はdecimal形式に変換されます。

＊注
整数演算では、二つの数を２進数に変換して計算し、その結果を１０進数に変換するだけでよいのですが、実数計算では、後述のように、指数や仮数など複雑な処理が必要になるので、処理時間が非常に遅くなります。科学技術計算を主とするコンピュータでは、実数計算に特化した演算回路をハードウェアで組み込み高速化を図っています。

浮動小数点数型の表示

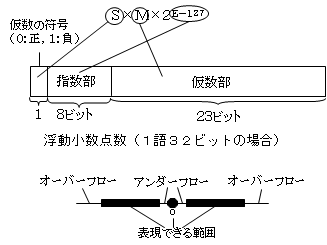
ＩＥＥＥ７５４（１語３２ビット）では、浮動小数点数の表現方法を次のように規定しています。
　符号は、正のとき０負のとき１とします。
　－６４０は、－１.２５×２^９ は－２.５×２^８ や－０.６２５×^１０ など、多様に表現できますが、仮数を１.Ｍのように整数部分を１になるように調整することを正規化といいます。そして、Ｍ（０.２５）の部分を２進数にしたものを仮数部に入れます。正規化を行うのは、仮数部（２３ビット）での有効桁数を大きくするためです。
　また、０.００１＝１.０２４×２^－１０ のように、絶対値が小さい数では指数が負になります。それで、２^０のときＥ＝１２７、２^１のときＥ＝１２８、２^－２のときＥ＝１２５などとなるように、元の指数に１２７を加えたＥを２進数にしたものを指数部（８ビット）に入れます。この操作をバイアスといいます。
　すなわち、－１.２５×２^９ を浮動小数点表示すると、次のようになります。
　　　Ｓ　Ｅ（指数部、８ビット）　Ｍ（仮数部、２３ビット）
　　　1 　　　　010001000　　　　　　0100 … 0000
　　（－）　（9＋127＝136）　　　　（1.25－1＝0.25）

例題

次のＩＥＥＥ７５４の３２ビットの浮動小数点型数は、１０進数ではいくつになるか。
　　　符号　指数部（８ビット）　仮数部（２３ビット）
　　　　0 　　　1000 0110　　　　0010 0000 … 0000

解答
符号が０→正数
指数部＝1000 0110₂＝１３４₁₀＝１２７＋７→２^７
仮数部＝0010 0000 … 0000₂＝２^－３＝０.１２５
これに整数部の１を加えて、１.１２５
答　１.１２５×２^７＝１４０.６２５

浮動小数点数の有効桁数

１０進数の小数点数は、２進数では循環小数になる場合があります。仮数部のビット数は有限ですから、切られてしまいます。それによる誤差を丸め誤差といいます。
　仮数部が２３ビットであり、整数部の１ビットを加えると２４ビットになります。２^２４≒１０^７ なので、１０進数での有効桁数は７桁になります（２進表示の桁数Ｂと１０進表示の桁数Ｄの間には、
　　　２^Ｂ＝１０^Ｄ　→　Ｄ＝Ｂ×log₁₀２ となります。log₁₀２≒０.３ですから、２４桁の２進数は１０進数では２４×０.３≒７桁になります）。
　また、浮動小数点数の計算では、多様な誤差が発生し、有効桁数は小さくなります。高精度が求められる場合には、１語を６４ビットとする倍精度浮動小数点型を用います。
　浮動小数点数による誤差については、誤差の種類で扱います。
　指数部での最大値は1111 1111₂＝２５５₁₀、最小値は0000 0000₂＝０₁₀です。バイアスを戻すと１２９、－１２８です。すなわち、絶対値が２^１２９ より大きいときはオーバーフロー、絶対値が２^－１２８ より小さい（０を除く）ときはアンダーフローとなり表現できないのです。倍精度浮動小数点型では指数部のビット数が大きいので、さらに大きい数や小さい数が表現できます。

オーバーフローとアンダーフロー

これまでに、いりいろなところでこの用語を使ってきました。整理すると、次のようになります。
　実数系では、上のように指数部が範囲を超えること、絶対値が非常に大か、非常に０に近いときに発生します。
　整数系では、１語のバイト数よりも大になってはみ出してしまうオーバーフロー、左側へのシフト（割り算）で末尾のビットがはみ出してしまうアンダーフローがあります。

単精度・倍精度

１語のバイト数を多くすることで、深刻なオーバーフローやアンダーフローの発生を抑えることができます。整数でも実数でも処理系により標準的なバイト数が決まっており、それを単精度といい、単精度の２倍のサイズを倍精度といいます。さらには特殊な用途では４倍精度をもつ処理系もあります。
　倍精度の計算は、内部で単精度の計算を複雑に組み合わせて実現しているので、計算時間は長くなります。