基数変換
人間は０～９の１０個の数字を用いた１０進法を用いていますが，「コンピュータは２進法だ」といわれます。入出力のときは１０進法になっていますが，コンピュータ内部では数値は２進法で取扱われているのです。
１０進法での１２３は（これを１２３１０のように表記する），
１×１００＋２×１０＋３
の意味です。もっと数学的な表現をすれば，
１×１０２＋２×１０１＋３×１００
となります。
それと同様に２進法では，たとえば１１０１２は
１×２３＋１×２２＋０×２１＋１×２０
＝１×８＋１×４＋０×２＋１×１
＝１３１０
となります。
それで，１０進法と２進法の変換を理解する必要があります。以下，その方法を学習しますが，次の表を覚えておくと便利です。
１０進数 ２進数 １６進数 １０進数 ２進数 １６進数
０ ０ ０ ８ １０００ ８
１ １ １ ９ １００１ ９
２ １０ ２ １０ １０１０ Ａ
３ １１ ３ １１ １０１１ Ｂ
４ １００ ４ １２ １１００ Ｃ
５ １０１ ５ １３ １１０１ Ｄ
６ １１０ ６ １４ １１１０ Ｅ
７ １１１ ７ １５ １１１１ Ｆ
１０進法、２進法などを一般化して、ｎ進法を定義することができます。そして、このｎを基数、異なる進数に変換することを基数変換といいます。
２進数と１０進数の基数変換
- ２進数の１１０１は，２を基数とする基数記数法ですから，その値は１×２３＋１×２２＋０×２１＋１×２０＝１×８＋１×４＋０×２＋１×１＝８＋４＋１＝１３となります。右のような表を作れば簡単に計算できます。
練習問題：２進数１０１１１→１０進数？ - １０進数→２進数：１３１０→１１０１２
-
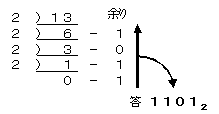１３＝８＋４＋１と分解すれば１１０１となることがわかりますが，そのような分解を容易にするためには，次のような手順を覚えておくと便利です。
- １０進数を２で割り，商と余りを求める。
- その商について，商が０になるまで「１」を繰り返す。
- 求めた余りを下から上に記述する。
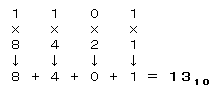２進数→１０進数（整数）：１１０１２→１３１０
１６進数と２進数、１０進数の基数変換
コンピュータ内部では２進数なのですが，２進数では桁数が非常に長くなるので，人間が取扱うのには不便です。それで２進数を１６進数に変換して表記することが多いのです。上表のように、４ビットは１桁の１６進数、１バイト（８ビット）は２桁の１６進数で表されます。
１０進数は０～９の１０個の数字があるから１０進法なのですし，２進数は０と１の２個の数字しかないので２進法なのだともいえます。すると１６進数では１６個の数字が必要になります。０～９までは１０進数と共通にし，１０をＡ，１１をＢ，・・・，１５をＦとしています。
- ２進数→１６進数
- ２進数の右端を基準して４個ずつに区切り，それぞれを上の表により１６進数にすればよいのです。たとえば，１１１１０１１２は，次のような操作により，７Ｂ１６となります。
１１１ １０１１
練習問題：２進数１１０１００１１→１６進数？
↓ ↓
７ Ｂ１１０１ ００１１
↓ ↓
Ｄ ３ ・・・答 Ｄ３１６ - １６進数→２進数
- １６進数の各桁の数字を４桁の２進数にすればよいのです。たとえばＤ３１６は，次の操作により１１０１００１１２となります。
Ｄ ３
↓ ↓
１１０１ ００１１ - １６進数→１０進数
- ２進数→１０進数と同じように考えます。７Ｂ１６を１０進数にするには，
７×１６＋１１＝１２３
とすればよいのです。Ｆ×１６＋Ｆ＝１５×１６＋１５＝２５５ - １０進数→１６進数
- これも１０進数→２進数と同じようにします。１２３１０を１６進数にするには，
１６ ）１２３ 余り
より，７Ｂ１６になります。
１６ ） ７ １１→Ｂ
０ ７