統計計算や数値解析など科学技術計算の分野では、誤差論という分野があるほど、誤差が大きな問題になります。
絶対誤差と相対誤差
誤差とは、本当の値(理論値)と近似値(計算値、測定値)との違いのことですが、誤差が大きいか小さいかを評価する尺度は2つあります。例えば理論値が10mの棒の計算値が11mだとしたとき、
絶対誤差=測定値-理論値=11-10=1m
相対誤差=(測定値-理論値)/理論値=(11-10)/10=0.1
で定義されます。
絶対誤差は計算が単純で誤差がmになるので物理的評価が容易です。ところが棒の長さが20mならば、1mの絶対誤差は相対誤差では0.05になります。そのため、棒の長さがまちまちなときは相対誤差のほうが適切な評価尺度になることがあります。
誤差の種類
自然界のデータは連続的な数値が多くあります。それをコンピュータで扱うときは、浮動小数点数で表現しますが、浮動小数点数は有限のビット数ですので、本当の数値ではなく近似値ですから、誤差を含んでいます。さらに、浮動小数点数同士の計算での誤差が生じます。
代表的な誤差には、丸め誤差、情報落ち誤差、桁落ち誤差、打切り誤差などがあります。
- 丸め誤差
- 丸め誤差とは、10進数の場合での四捨五入のような理由により、厳密には真の値をとることができない誤差のことです。
- コンピュータでは、一つの数値を2バイトや4バイトなど有限の長さをもつ「語」に保存されるため、πや√2などの無理数を正しく表現できません。
- 科学技術計算では、浮動小数点型(説明)のデータを用いますが、これは2進法により数値を表現します。そのため、10進数の0.1や1/3などは2進数では循環小数になるので、真の値にはなりません。
- 浮動小数点の演算では、有効数字が限定されます。そのため、3.1415926535などを正確に表現することができません。
|a-b|<ε (ε=0.0001のような小さな数)
のようにする必要があるのです。
浮動小数点数
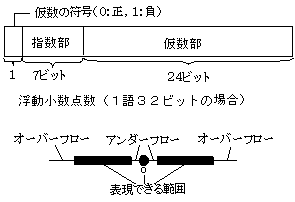
固定小数点型では,取扱える数値が限定されますし,非常に大きな数や小さい数を取扱うことができませんので,科学技術計算などでは困ります。このような数値を表現するには,浮動小数点型を用います。
浮動小数点型では,0.6022×1024のように,数値をR=M×BEという形式で表現します。ここでMを仮数,Bを底,Eを指数といいます。内部表現では,Mは0~1の16進数,Mは16,Eは16進数にした値に64を加えるなど,面倒な変換が必要になりますが,それを右図のような形式で表現します。
この場合は,0000000のときは-64ですので10-77,1111111のときは63で1076となるので,浮動小数点型で取扱える数は,
-1076~-10-77,0,10-77~1076
の範囲になります。絶対値が1076を超えるとオーバーフロー,絶対値が10-77より小さいとアンダーフローとなり,取扱うことができません。
また(後述のように),10進小数点数を2進数に変換すると丸め誤差を生じます。2進数の24桁は10進数の7桁程度ですので,有効数字は7桁程度になります。たとえば,3.1415926535などの値を入力しても,コンピュータ内部ではそれを正確に受け取ることはできないのです。 - 情報落ち誤差
- 絶対値の非常に大きな数と小さな数の加算を行ったとき,小さい数が計算結果に反映されないために発生する誤差のことです。
浮動小数点の仮数部の有効桁数を3桁としたとき、1230000も0.0123も有効桁数が3ですが、
1230000+0.0123=1230000.0123
の結果は正しく計算できません。
絶対値が大きく異なる多数の数値を加減算するときには、絶対値の小さい順に行うのが適切です。 - 桁落ち誤差
- 桁落ち誤差とは、近い値をもつ浮動小数点数の減算などにより、有効桁数が小さくなることによる誤差です。
例えば、a=12.34567には、εa=0.000005の絶対誤差があります。それで、aの相対誤差は、
|εa/a|=0.000005/12.34567=0.0000004
になります。同様に、b=12.34556の絶対誤差は、εb=0.000005になります。 それに対して、a-b=0.00011になり、有効桁数は2桁になるので、その相対誤差は、
(|εa|+|εa|)/(a-b)=0.00001/0.00011=0.09
となってしまいます。 - 打切り誤差
- 浮動小数点数の計算処理の打ち切りを、指定した規則で行うことによって発生する誤差のことです。
例えば、方程式 f(x)=0 を解くには、x0→x1→x2→・・・→xnのように逐次的に真の根に近づくアルゴリズムを用います。
このとき、浮動小数点演算ですので、f(xn)=0 になることは期待できませんし、無限ループになってしまうこともあります。それを回避するために、小さい数εを与えて、
|f(xn)|<ε
|xn-xn-1|<ε
|(xn-xn-1)/xn|<ε
などのようにします。このような理由により容認した誤差を打切り誤差といいます。
数値解析のような浮動小数点演算を行うアルゴリズムでは、前述した計算量を小さくするとともに、このような誤差の累積が演算過程により増大しないように工夫することが重要です。また、その利用にあたっては、実用の観点から打切りの基準を考えること、εの値を考慮することが必要です。