Ｗｅｂ教材一覧＞アルゴリズム
（ＢＯＫ大区分：１　基礎理論、中区分：２　アルゴリズムとプログラミング、中区分：２　アルゴリズム）

アルゴリズム

キーワード

アルゴリズム、疑似言語、流れ図、決定表（デシジョンテーブル）、プログラム、バイナリサーチ、再帰、階乗

アルゴリズムとは

アルゴリズム（algorithm）とは、問題を解くための手順を明確に述べたものです。解法のロジックといってもよいでしょう。アルゴリズムをコンピュータに行わせるために、コンピュータ言語で記述したのがプログラムです。
　広義には、給与計算や会計計算などもアルゴリズムだといえますが、一般的には、データを小さい順に並べ替えるとか、方程式の根を求めるなど、よく用いられる処理手順のことを指します。
　アルゴリズムを示すには、
　　　文章による表現
　　　決定表（デシジョンテーブル）
　　　流れ図（フローチャート）
　　　ソースプログラム
などがあります。

疑似言語

文章による表現は汎用的ではありますが、複雑なアルゴリズムを記述するのには不向きです。
　それで、自然言語ではなく、プログラミング言語に似た形式で記述すれば、厳密ではなくても大体のロジックを示すことができます。しかも、留意すべき事項を自然言語で記述することもできます。そのような表現を疑似言語といいます。
　疑似言語の仕様は、作成者が勝手に決めてよいのですが、関係者が共通に理解できるような仕様にするのが適切です。

下は、事前に中計キー、小計キーでソートされているファイルを読んで、明細行、小計、中計、総計の表を出力するプログラムのロジックを疑似言語で記述したものです。

メインプログラム
　　総計累計項目 = 0　　　　　
　　call ファイル読込
　　while (データがある間) {
　　　　前中計キー = 中計キー
　　　　中計累計項目 = 0
　　　　while (中計キー == 前中計キー) {
　　　　　　前小計キー = 小計キー
　　　　　　小計累計項目 = 0
　　　　　　while ((中計キー == 前中計キー) and (小計キー == 前小計キー)) {
　　　　　　　　call 明細行処理
　　　　　　　　小計累計項目 = 小計累計項目 + 明細累計項目
　　　　　　　　call ファイル読込
　　　　　　}
　　　　　　call 小計処理
　　　　　　中計累計項目 = 中計累計項目 + 小計累計項目
　　　　}
　　　　call 中計処理
　　　　総計累計項目 = 総計累計項目 + 中計累計項目
　　}　　
　　call 総計処理
サブルーチン
　　ファイル読込
　　　　中・小計キー、明細累計項目の定義
　　　　ファイルのデータがなくなったときのフラグ設定
　　明細行処理
　　　　明細行累計項目間の計算と出力
　　小計処理
　　　　小計累計項目間の計算と出力
　　中計処理
　　　　中計累計項目間の計算と出力
　　総計処理
　　　　総計累計項目間の計算と出力

流れ図（フローチャート）

アルゴリズムとは処理の順序を示したものだといえます。流れ図とは、処理の流れを図化したものです。その表記法はＪＩＳ規格になっています。処理は長方形、分岐はひし形にように決められた図形があり、それらの間の流れを線や矢印で表します。
　その例は、下の「バイナリサーチ」の図を見てください。
　なお、すべてのアルゴリズムは、「順次」「選択（条件分岐）」「反復（繰り返し）」の３つのパターンを組み合わせることで表現できることが証明されています（参照：「プログラムの制御構造」）。

決定表（デシジョンテーブル）

ある事象について条件の組合せとそれに対する処理を表形式で整理したものです。複雑な条件を図表化することにより、理解をしやすくするとともに、プログラムを体系的にし簡素化できる利点があります。

　　　　　　　　　　　　　　　Ａ　Ｂ　Ｃ　Ｄ
　　　　　　┌─┬─────┰─┬─┬─┬─‪┐
　　　　　　│　│面接≧良？┃Ｙ│Ｙ│Ｙ│Ｎ│
　　　　　　│条├─────╂─┼─┼─┼─┤
　　　　　　│　│体力≧良？┃Ｙ│Ｙ│Ｎ│－│
　　　　　　│件├─────╂─┼─┼─┼─┤
　　　　　　│　│学力≧良？┃Ｙ│－│－│－│
　　　　　　┝━┿━━━━━╋━┿━┿━┿━┥
　　　　　　│　│採用　　　┃Ｘ│－│－│－│
　　　　　　│処├─────╂─┼─┼─┼─┤
　　　　　　│　│補欠　　　┃－│Ｘ│－│－│
　　　　　　│理├─────╂─┼─┼─┼─┤
　　　　　　│　│不採用　　┃－│－│Ｘ│Ｘ│
　　　　　　└─┴─────┸─┴─┴─┴─┘

　　Ａ：面接、体力、学力のすべてが良以上ならば採用
　　Ｂ：面接と体力が良以上なら学力に関係なく補欠
　　Ｃ：面接が良以上だが体力が良未満なら学力に関係なく不採用
　　Ｄ：面接が良未満なら体力・学力に無関係に不採用

ソースプログラム

ソースプログラムでの表示では、それで実際に動作し確認できるので最適な方法ではありますが、これを作成することが目的なのですから、順序が逆だともいえます。ソースプログラムが使われるのは、大きく二つの局面です。

解読性の向上
作成したプログラムをウォークスルーでチェックしたり、プログラムの改訂をしたりする場合、関係者が容易に解読できることが重要です。そのために「コーディング規約」に準拠した記述をすること、適切なコメント文を挿入するなどが求められます。
特定個所の説明
部分的に難解あるいは特殊なプログラム技術を要する部分は、技術力の高いプログラマが記述し、サブプログラムのような形式にして、通常のプログラマは内容のロジックを理解できなくても、パラメタの指定など使い方さえ理解しておけばよいとすることができます。

アルゴリズムの例

バイナリサーチ

アルゴリズムを、バイナリサーチという探索方法を例にして説明します。
（バイナリサーチの厳密なアルゴリズムに関しては、「サーチ」（al-search）を参照のこと）

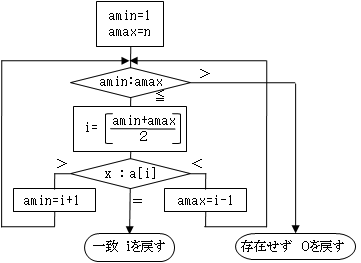
　サーチとは、学籍番号が配列ａに入っているとして、ある学籍番号ｘを与えて、それに一致する要素ａ[ｉ]の要素番号ｉを探すような処理です。ここでは、配列の大きさ（学生の人数）をｎとし、学籍番号の小さい順に並んでいるとします。バイナリサーチとは、次のようなアルゴリズムです（文章による表現）。

最小値の要素はａ[1]なので、amin＝１、最大値の要素はａ[n]なので、amax＝ｎとする。
求めるｉは、amin≦ｉ≦amax の間に存在する。
i＝(amin＋amin）とし、ａ[i]（すなわち配列の探索範囲の中央要素）とｘを比較する。
ｘ＝ａ[i] ならば完了する。
２の比較で、ｘ＜ａ[i] ならば、求める要素は、これよりも前にあるのだから、amax＝i-1 として２へ行く。
ｘ＞ａ[i] ならば、求める要素は、これよりも後にあるのだから、amin＝i+1 として２へ行く。

これを流れ図で表現すると、右図のようになります。このほうがわかりやすいでしょう。
　さらに、プログラム（JavaScript）にすると、次のようになります。

　　　amin = 1; amax = n;
　　　while (amin <= amax) {
　　　　　i = Math.floor((amin + amax)/2);
　　　　　if (x == a[i]) return i; /* 一致した。ｉを戻す */
　　　　　else if (x < a[i]) amax = i - 1;
　　　　　else amin = i + 1;
　　　｝
　　　return 0; /* 一致する要素なし */

再帰を用いたアルゴリズム

アルゴリズムでの基本的手法の一つに再帰（recursive）があります。「ｎ－１までが正しいと仮定したら、ｎの場合も正しいことを証明すれば、すべてのときに正しいといえる」という数学的帰納法と似た考え方です。ｎでの問題をｎ－１での結果を用いて解くアルゴリズムを考えればよいのです。
　プログラムでは、再帰とは、Ａというものを定義するとき、Ａの定義のなかでＡ自体を含むことをいいます。プログラムでいえば、ある関数Ａのなかで、関数Ａを呼び出しているとき、再帰プログラム（再帰関数）といいます。

　再帰関数の典型的な例が階乗関数です。階乗とは、
　　　Ｆ(ｎ)＝ｎ！＝１×２×３×…×ｎ　　　　・・・ア
のことですが、
　　　ｎ！＝（１×２×３×…×(ｎ－１))×ｎ
　　　　　＝ｎ×(ｎ－１)！
ですから、
　　　　　　　┌１　　　　　　　　（ｎ＝０のとき）
　　　Ｆ(ｎ)＝│　　　　　　　　　　　　　　　・・・イ
　　　　　　　└ｎ×Ｆ(ｎ－１)　　（ｎ≧１のとき）
と再帰的に定義することができます。

再帰を用いた階乗のプログラムは次のようになります。
　　function f(n);
　　　　if (n==0) return 1;
　　　　else return n * f(n-1);
　　}

再帰アルゴリズムを用いることには、次のような利点があります。
　　・アルゴリズムを発見しやすくなる。
　　　　→プログラムが作りやすい。
　　・一般に、アルゴリズムが簡素になる。
　　　　→プログラムの誤りが少なくなる。
　しかし、プログラムが簡潔であることは、必ずしも実行効率がよいことではありません。上のプログラムでｆ(５) をを実行するには、ｆ(４)，ｆ(３)，…，ｆ(３) を実行しなければないません。関数を呼び出す回数が増加しますし、それらの結果を保存しておく必要があります。処理のための時間やメモリ容量は、むしろ増大してしまいます。

参照：「再帰アルゴリズム」

計算量（オーダー）

典型的なアルゴリズム

このシリーズでは、典型的なアルゴリズムを紹介し、それを通してアルゴリズムの考え方を学習することを目的としています。いくつかのアルゴリズムには、簡単なプログラムを用意しましたので実験もできます。

ソート

ソートとは、データを小さい順（昇順）、大きい順（降順）に並べ替えることです。まず、「ソートの基礎」で、選択ソートを例にして、アルゴリズムの理解を高めることを目的にします。

ソートの方法には、多様な方法があります（→参照：「ソートの種類」）。選択ソートに類似した有名な方法にバブルソートや挿入ソート（→参照：「基本的なソート方法」）、高速なソート方法では、クイックソートやシェルソートなど（→参照：「高速ソート」）があります。

マージ

マージとは、既にソートされている二つの配列を、一つの配列にすることです。例えば、学生番号の昇順でソートされている男子生徒の表と女子生徒の表をマージして、男女全体で学生番号の昇順にソートされた一つの表にまとめる操作です。
　先のソートは、配列を対象にしていましたが、このマージの考え方を用いることにより、ファイルを対象にしたソートもできます（→参照：「マージと外部ソート」）。

順位づけ

通常のソートは、元の配列要素を変更する処理ですが、配列自体はそのままにしておき、小さい順の番号や、自分の次になる要素の位置を示す情報を与えると便利なことがあります。後者はポインタという概念であり、データ構造の一つであるリスト構造に発展します（→参照：「順位づけ」）。

サーチ

サーチとは、探索のことで、配列ａのなかで、与えた値ｘと同じ値をもつ要素ａ[ｉ]を探し、その要素番号を求める操作です。代表的なアルゴリズムであるリニアサーチ（順次探索法）とバイナリサーチ（二分探索法）を取り扱います（→参照：「サーチ」）。

素数、文字列探索の基礎

その他のポピュラーなアルゴリズムとして、ユークリッドの互除法、エラトステネスのふるい、文字列の検索を紹介します。（→参照：「素数、文字列探索の基礎」）。

　これらは古典的なアルゴリズムですが、この応用分野は広く、その拡張化や高速化が行われています。情報処理技術者試験よりもやや高度ですが、参考までに紹介しておきます。
　　ユークリッドの互除法：（→発展：「ユークリッドの互除法」）
　　エラトステネスのふるい：（→発展：「素数アルゴリズム」）
　　文字列探索：（→発展：「文字列探索」）

数値解析

連立方程式の解法や定積分の求値法など、数学の分野では多くのアルゴリズムがありますが、別シリーズ「数値解析」で扱うことになして、ここでは割愛します。

過去問題：「アルゴリズムとプログラミング」

（このシリーズからみると、やや初歩的ですが、ＩＴパスポート試験の問題も掲げておきました）

アルゴリズムへ