再帰アルゴリズム

アルゴリズムでの基本的手法の一つに再帰（recursive）があります。再帰とは、Ａというものを定義するとき、Ａの定義のなかでＡ自体を含むことをいいます。プログラムでいえば、ある関数Ａのなかで、関数Ａを呼び出しているとき、再帰プログラム（再帰関数）といいます。

再帰プログラムの説明－階乗を例にして

再帰の説明

　再帰関数の典型的な例が階乗関数です。階乗とは、
　　　Ｆ(ｎ)＝ｎ！＝１×２×３×…×ｎ　　　　・・・ア
のことですが、
　　　ｎ！＝（１×２×３×…×(ｎ－１))×ｎ
　　　　　＝ｎ×(ｎ－１)！
ですから、
　　　　　　　┌１　　　　　　　　（ｎ＝０のとき）
　　　Ｆ(ｎ)＝│　　　　　　　　　　　　　　　・・・イ
　　　　　　　└ｎ×Ｆ(ｎ－１)　　（ｎ≧１のとき）
と再帰的に定義することができます。

プログラム

アによるプログラムは
　　function f(n);
　　　　if (n==0) return 1;
　　　　fact = 1;
　　　　for (i=1; i<=n; i++) {
　　　　　　fact = fact * i;
　　　　}
　　　　return fact;
　　}
となりますが、イのように再帰を用いると
　　function f(n);
　　　　if (n==0) return 1;
　　　　else return n * f(n-1);
　　}
となります。

再帰とスタック

再帰を配列に入れながら処理をする場合、スタックあるいはＬＩＦＯ（後入先出）配列を用いるのが適切です。階乗関数 f(3) の計算では次のようになります。
　　│f(3)││f(2)││f(1)││F(0)=1│　│1x1=1 ││1x2=2 ││2x3=6 │
　　└──┘├──┤├──┤├───┤　├───┤├───┤└───┘
　　　　　　│　3 ││　2 ││　1 　│　│　2 　││　3 　│
　　　　　　└──┘├──┤├───┤　├───┤└───┘
　　　　　　　　　　│　3 ││　2 　│　│　3 　│
　　　　　　　　　　└──┘├───┤　└───┘
　　　　　　　　　　　　　　│　3 　│
　　　　　　　　　　　　　　└───┘
　　────── push ───────→　────── pop ─────→

再帰の利点と欠点

再帰は、「ｎ－１までが正しいと仮定したら、ｎの場合も正しいことを証明すれば、すべてのときに正しいといえる」という数学的帰納法と似た考え方です。ｎでの問題をｎ－１での結果を用いて解くアルゴリズムを考えればよいのです。
　そのため、再帰アルゴリズムを用いることには、次のような利点があります。
　　・アルゴリズムを発見しやすくなる。
　　　　→プログラムが作りやすい。
　　・一般に、アルゴリズムが簡素になる。
　　　　→プログラムの誤りが少なくなる。
　　　　　他人が読んでわかりやすいプログラムになる。
　このような利点を実感するために、代表例として、「ソート」と「ハノイの塔」を後述します。

しかし、プログラムが簡潔であることは、必ずしも実行効率がよいことではありません。イのプログラムで ｆ(５) をを実行するには、ｆ(４)，ｆ(３)，…，ｆ(３) を実行しなければないません。関数を呼び出す回数が増加しますし、それらの結果を保存しておく必要があります。処理のための時間やメモリ容量は、むしろ増大してしまいます。その代表的な例として「フィボナッチ数列」を後述します。

ソート

ソート（整列）とは、データを小さい順あるいは大きい順に並べ替えることです。多様な方法があります（「ソートの種類」参照）が、ここでは、それらを知らなくても、再帰の考え方を用いると、比較的容易にプログラムを作ることができることを説明します。

アルゴリズム

配列ａを小さい順にソートすることを考えます。これまでに、ｎ－１個までは既にソートされているとき、要素ａ[ｎ] について考えます。
　　　　１　　２　　３　　　　　n-1 　　ｎ
　　　┌──┬──┬──┬──┬──┐┌──┐
　　　│１０│２０│４０│５０│６０││a[i]│
　　　└──┴──┴──┴──┴──┘└──┘

次のようにすればよいことは、容易に気づくでしょう。
　ａ[ｎ]＝８０のように、ａ[ｎ－１] ≧ ａ[ｎ] の場合は、ｎも含めてソートされているので、何もしなくてよいことになります。
　ａ[ｎ]＝３０のように、ａ[ｎ－１] ＜ ａ[ｎ] の場合は、下図の操作を行ないます。
　　　　　　　１　　２　　３　　　　　n-1 　　ｎ
　　　　　　┌──┬──┬──┬──┬──┐┌──┐
　　　　　　│１０│２０│４０│５０│６０││３０├┐
　　　　　　└──┴──┴─┬┴─┬┴─┬┘└──┘│①
　　　　　　　　　　　　②　└┐　└┐　└┐　　　　│
　　　　１　　２　　ｉ＝３　　│　③│　　│ｎ　　┌┴┐
　　　┌──┬──┐┌──┐┌┴─┬┴─┬┴─┐　│ｗ│
　　　│１０│２０││３０││４０│５０│６０│　└┬┘
　　　└──┴──┘└─┬┘└──┴──┴──┘　　│
　　　　　　　　　　　④└─────────────┘

1. ａ[ｎ] の値３０を一時的にｗに保管しておきます。
2. 配列の先頭から順にａ[ｉ] ≧ａ[ｎ] の間ｉをずらしていき、ａ[ｉ] ＜ａ[ｎ] となる個所ｉを見つけます。（図ではｉ＝３）
3. 要素ｉ～ｎ－１を右に１つずらして、ｉ＋１～ｎに入れます。このとき右のほうからずらさないと、データが消えてしまいます。
4. ａ[ｎ] の値を保管していたｗの値を ａ[ｉ] に入れます。

プログラム

上のアルゴリズムをプログラムにするのは容易です。

　　function sort(n) {
　　　　if (n==1) return;
　　　　sort(n-1);　　　　　　　──再帰：ｎ－１までがソートされていると仮定
　　　　w = a[n]; 　　　　　　　　　　　　　　　　　　　①
　　　　if (w <= a[n-1]) { 　　──ａ[ｎ－１] ＜ ａ[ｎ] の場合だけを考えればよい
　　　　　　i = 1;
　　　　　　while((i < n) && (a[i] <= w)) i++;　　　　　②
　　　　　　for (j=n-1; j>=i; j--) a[j+1] = a[j]; 　　　③
　　　　　　a[i] = w; 　　　　　　　　　　　　　　　　　④
　　　　}
　　}

ハノイの塔

かなり難解な問題が再帰を用いることにより、非常に簡単になる例として、「ハノイの塔」があります。
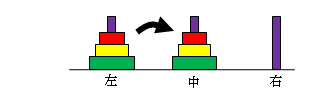
　図のように、右の棒にｎ枚の円盤が積んであります。
　　・１回に１枚の円盤しか動かせない。
　　・小さい円板の上に大きい方の円盤を置いてはならない。
の規則に従って，円盤をＡからＢに移動せよという問題です。

プログラム

再帰を用いたプログラムは非常に簡単です。
　ここでは円盤の小さい順に円盤番号ｎをつけています。

　　function hanoi(n, a, b, c) {
　　　　if (n==0) return;
　　　　hanoi(n-1, a, c, b);
　　　　document.write("円盤" + n + "：　" + a + "　→　" + b + "<br />");
　　　　hanoi(n-1, c, b, a);
　　}

トレース

「hanoi(4, "左", "中", "右")」を実行した結果を示します。
　ア　円板1：　左　→　右
　イ　円板2：　左　→　中
　ウ　円板1：　右　→　中
　エ　円板3：　左　→　右
　オ　円板1：　中　→　左
　カ　円板2：　中　→　右
　キ　円板1：　左　→　右
　ク　円板4：　左　→　中
　ケ　円板1：　右　→　中　　　　　　─┐
　コ　円板2：　右　→　左　　　　　　　│
　サ　円板1：　中　→　左　　　　　　　│
　シ　円板3：　右　→　中　　　　　　　│ｎ＝３
　ス　円板1：　左　→　右　─┐　　　　│
　セ　円板2：　左　→　中　　│ｎ＝２　│
　ソ　円板1：　右　→　中　─┘　　　─┘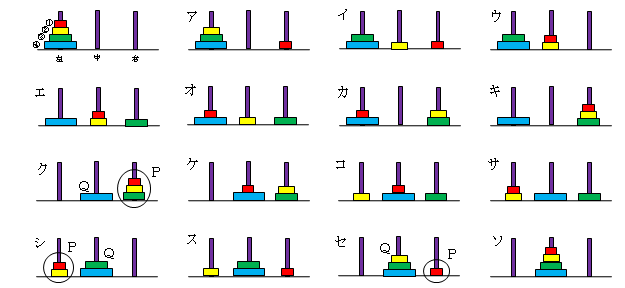

アルゴリズム

円盤がｎ個あるとき、１～ｎ－１の円盤を一つの円盤であるとして、１～ｎ－１の円盤をＰ、ｎ番目の円盤をＱとすれば、２個の円盤を移動することだと考えることができます。
　２つの円盤ＰとＱがａの棒にあるとして、それをｂの棒に正しく移動するには、次の３つの操作を行えばよいことは明白です（左中右などの物理的意味を排除するために、あえてａ，ｂ，ｃとします）。
　　操作１：ＰをＡからＣへ移動
　　操作２：ＱをＡからＢへ移動
　　操作３：ＰをＣからＢへ移動

hanoi(ｍ, ａ, ｂ, ｃ) とは、ａからｂへ移動することだと定義すれば、document.write（～）がそれにあたります。
　そして、Ｐの移動とはｎ－１のときの移動のことですから、
　　操作１：hanoi(n-1, a, c, b);
　　操作３：hanoi(n-1, c, b, a);
となります。

トレースでのクでは、円盤４（Ｑ）が既に中に置かれているとすれば、３つの円盤（Ｐ）を移動させることであり、ク以降の操作は、円盤数ｎが３のときの問題を解くことだといえます。同様にシ以降はｎ＝２、セ以降はｎ＝１を解くための操作になっています。

ハノイの塔の問題を、再帰の概念を使わずにアルゴリズムを考えるのは、かなりの難問でしょう。それが、再帰の概念により、ｎ個の円盤の問題を、ｎ－１個の問題にすることができ、結局は２個の円盤での問題にすることができ、上掲のようなきわめて簡単なアルゴリズムにすることができるのです。

フィボナッチ数列

再帰による処理効率の低下の例（再帰を使うべきではない例）として有名なのがフィボナッチ数列です。フィボナッチ数列とは、
　　　１，１，２，３，５，８，１３，２１，…
の数列で、１＋１＝２，１＋２＝３，２＋３＝５のように、直近の２つの数を加えたものです。それで、
　　　　　　　┌１　　　　　　　　　　　　　（ｎ＝１のとき）
　　　Ｆ(ｎ)＝│１　　　　　　　　　　　　　（ｎ＝２のとき）
　　　　　　　└Ｆ(ｎ－１) ＋ Ｆ(ｎ－２)　　（ｎ≧３のとき）
と定義できます。

プログラム

再帰を用いないならば、１つ前の数をｘ１，２つ前の数をｘ２として、プログラムｆ１にすることができます。
　　function f1(n);
　　　　if (n<=2) return 1;
　　　　x1 = 1; x2 = 1;
　　　　for (i=3; i<=n; i++) {
　　　　　　x = x1 + x2;
　　　　　　x2 = x1;
　　　　　　x1 = x;
　　　　}
　　　　return x;
　　}
となります。

再帰を用いたプログラムｆ２は、
　　function f2(n);
　　　　if (n<=2) return 1;
　　　　else return f2(n-1) + f2(n-2);
　　}
となります。

計算量の比較

計算量を forループ のなかの３つで代表させるならば、ｆ１での計算回数は、３ｎ回です。
　それに対してｆ２の計算回数は、ほぼフィボナッチ数列での値と同じ程度の回数になります。
　ｎが大きい場合、例えばｎ＝３０のときでは、ｆ２ならば９０回なのに、ｆ１では（ｎ＝３０のフィボナッチ数は）８３２,０４０回になってしまいます。