スタートページ＞ JavaScript＞ ライブラリ目次

確率統計分布関連 JavaScript関数ライブラリ stat.js の利用解説書

ご利用にあたって

一般分布

正規分布
　　確率密度　p = distNormalDen(x [,μ, σ]);
　　累積確率　s = distNormalCum(x [,μ, σ]);
　　累積確率の逆関数　x = distNormalInv(p [,μ, σ]);

μ、σを省略すると、μ＝０、σ＝１の標準正規分布になります。
確率密度
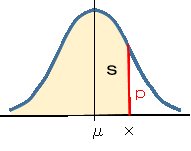
　平均μ、分散σ2の正規分布において、値ｘの確率密度関数の値ｐは次式で計算できます。
　　p = 1/√(２πσ2) * e(-(x-μ)2/2σ2)
累積確率
　－∞～ｘの累積確率の値ｓを戻します。
　確率密度 を数値積分 sFx() で計算するより、近似式が知られています。
　ここではHastingsの式を使いました。（引用先：http://qiita.com/gigamori/items/e17e6f9faffb78822c56　by Yanai Takamichi）
累積確率の逆関数
　累積確率 s を与えたときの x を戻します。
　次の近似式を参考にさせていただきました
　「https://potatodigger.wordpress.com/2013/06/30/正規分布の確率密度関数pdf、累積分布関数cdf、逆累/　by potatodigger」

μ= σ=指定しないとμ＝０、σ＝１
x= p= s=
(x→p)　 (x→s)　 (p→x)　

中心極限定理による必要標本数と許容確率誤差
　　必要標本数：　[n5, n1] = distCltNmin(p, pe)　
　　許容確率誤差：[pe5, pe1] = distCltPerr(p, n)　

　　n ：必要な標本数　n1:有意水準５％, n1：有意水準１％
　　p ：母集団での想定発生確率
　　pe：許容確率誤差 = 標本での発生確率と母集団での想定発生確率の差　pe1:有意水準５％, n1：有意水準１％
　　pt：有意水準(= 0.05, 0.01）(Ｚ；正規分布の変位。 両側有意水準 pt = 0.05 のとき Ｚ = 1.96、 pt = 0.01 のとき Ｚ = 2.58）

中心極限定理：母集団の分布に関係なく、標本数 n が非常に大きくなると，標本平均の分布は平均μ，分散 σ2／ｎ の正規分布に近づく。
　標本の大きさ n が大であれば標本比率 p0 は近似的に正規分布 (p, p(1-p)/n) に従う。
　必要な標本数　n = (Ｚ/pe)2 * p(1-p)
　ｎを与えたときの確率誤差　pe = Ｚ*√(p(1-p)/n)
(Ｚ；正規分布の変位。 両側有意水準 pt = 0.05 のとき Ｚ = 1.96、 pt = 0.01 のとき Ｚ = 2.58）

母確率が p ± pe と想定されるときに必要な標本数
p= pe= n0.05= n0.01=
母確率が p と想定されるときに、標本数を n としたときの、信頼区間 p ± Perr の Perr
p= n= Perr0.05= Perr0.01=

三角分布
　　平均分散： [平均, 分散] = distTriMV(xmin, xmax, xmod);
　　確率密度： p = distTriDen(x, xmin, xmax, xmod);
　　累積確率： s = distTriCum(x, xmin, xmax, xmod);
　　累積確率の逆関数： x = distTriInv(s, xmin, xmax, xmod);

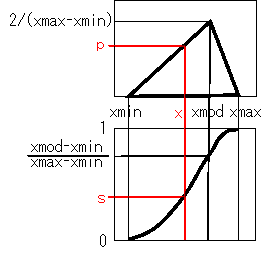
右図のように、３点 ａ(xmin,0), ｂ(xmax,0), ｃ(xmod, h) を結ぶ三角形となる分布。
　　平均：(a+b+c)/3、　分散：(a2+b2+c2-ab-bc-ca)/18
参照：「三角分布」

最小値：xmin= 最大値：xmax= 最頻値：xmod=
ｘ＝ ｐ＝ ｓ＝ 平均＝ 分散＝
(→平均,分散)　 (x→p)　 (x→s)　 (s→x)　

作表

上の xmin, xmax, xmod を与えたとき、x=xmin～xmax における p と s のリストを表示します。

二項分布
　　平均分散： [平均, 分散] = distBinMV(n, p);
　　確率密度：Px = distBinDen(x, n, p);
　　累積密度：s = distBinCum(x, n, p);

平均：ｎｐ　　分散：ｎｐ(１－ｐ)
発生確率がｐの事象が、ｎ回の試行でｘ回発生する確率
　　確率密度： ｘ回発生する確率　　　Ｐ(x) = nＣx・px(1-p)n-x
　　累積密度： ０～ｘ回発生する確率　Ｓ(≦x) = ΣＰ(x)
　　　　nＣx = n!/x!(n-x)! = nCx(n, x)　　二項係数（ｎ個からｘ個を取り出す場合の数（場合の数））
　　参照：「離散型統計分布」
二項分布の計算は計算量が大きく、大きい数と小さい数の計算が必要になるので誤差が生じます。計算を容易にするために、
　　・np > 5 かつ n(1-p) > 5 ならば、平均μ=np、標準偏差σ=√np(1-p) の正規分布で近似できる。
　　　確率密度：区間 x-0.5～x+0.5 の正規分布累積確率　distNormalCumMinmax(x-0.5, x+0.5, μ, σ)
　　　累積密度：≦x+0.5 の累積確率 distNormalCum(x+0.5, μ, σ)
　　・n>50, np≦5 ならば、平均λ=np のポアソン分布で近似できる。
などの方法がありますが、ここでは用いていません。

n= p=
x= Px= s= 平均＝ 分散＝
(→平均,分散)　 (x→Px)　 (x→s)

作表

上の n,p を与えたとき、x=0～n における Px と s のリストを表示します。

負の二項分布
　　平均分散： [平均, 分散] = distBinNegMV(x, p);
　　確率密度： Pn = distBinNegDen(x,n,p);
　　累積密度： s = distBinNegCum(x,n,p);

平均：ｘ(１－ｐ)／ｐ　　分散：ｘ(１－ｐ)／ｐ2
ある事象が起こる確率がｐのとき、ｎ回試行したときに、その事象がはじめてｘ回になる確率Ｐ(n)の確率分布。
　　　Ｐ(n) = n-1Ｃx-1・ｐx(1-p)n-x
参照：「離散型統計分布」
x=1 のときは、幾何分布 distGeoDen と一致します。

n= p=
x= Pn= s= 平均= 分散=
(→平均,分散)　 (x→Pn)　 (x→s)

作表

上の n,p を与えたとき、x=1～n における Pn と s のリストを表示します。

幾何分布
　　平均分散：[平均, 分散] = distGeoMV(n, p);
　　確率密度 Pn = distGeoDen(n, p);
　　累積確率 s = distGeoCum(n, p);
　　累積確率の逆関数　n = distGeoInv(s, p);

平均：(１－ｐ)／ｐ　　分散：２*平均2
発生確率ｐの事象がはじめて発生したときの試行回数ｎの確率分布（負の二項分布で、x＝１とおくと、幾何分布に一致）
　　確率密度： Pn = (1-p)n-1*ｐ
　　累積確率： s = 1-(1-p)n
逆関数：　 n = log(1-s) / log(1-p)
参照：「離散型統計分布」

n= p=
Pn= s= 平均= 分散=
(n.p→平均,分散)　 (n.p→Pn)　 (n.p→s)　 (s→n)

超幾何分布
　　平均分散：[平均, 分散] = distHyperGeoMV(a, b, α);
　　確率密度： p = distHyperGeoDen(a, b, α, β);
　　累積確率： s = distHyperGeoCum(a, b, α, β);

平均・分散
　a+b 個から α個取り出すとき、白玉(a)　がαである確率 P(α) の平均・分散
　　平均 = x*a/n;　　分散 = (a*(a-1) * x*(x-1)) / (n*(n-1));
確率密度
　袋の中にＡがａ個、Ｂがｂ個入っている。α＋β個を取り出したとき、Ａがα個、Ｂがβ個である確率
　　　p = aＣα・bＣβ／a+bＣα+β
　で計算できる（参照：「離散型統計分布」）。
確率密度：αが０～α個である確率。
「α以上である確率」は distHyperGeoCum(a, b, α-1, β+1) になる。
超幾何分布では、ＣやＤなど多数の系列も対象にするが、複雑になるので、ここでは２系列に限定する。

　　Ａ　　Ｂ
袋の中の個数： a = b =
取り出した個数： α= β=
ｐ＝ ｓ＝ 平均＝ 分散＝

指数分布
　　平均分散：[平均, 分散] = distExpMV(λ);
　　確率密度：　p = distExpDen(t, λ)　
　　累積確率：　s = distExpCum(t, λ)　
　　累積確率の逆関数：　t = distExpInv(p, λ)　

平均 = 1/λ;　　分散 = 1/λ2;

関数一般形式　機能　計算式
distExpDen(t, λ)　t=t における確率密度　p = λ*e(-λ*t)
distExpCum(t, λ)　区間 t=0～t の累積確率　s = 1-e(-λ*t)
distExpInv(p, λ)　累積確率が p となる t の値　t = -(1/λ)log(1-p)
参照：「ポアソン分布と指数分布」

λ= t= p= s= 平均= 分散=
(λ→平均,分散)　 (t,λ→p)　 (t,λ→s)　 (p,λ→t)

作表

上の λ を与えたとき、ｔ を変化させたときの p と s のリストを表示します。

アーラン分布
　　平均分散：[平均, 分散] = distErlangMV(λ, k);
　　確率密度：　p = distErlangDen(t, λ, k)　
　　累積確率：　s = distErlangCum(t, λ, k)　

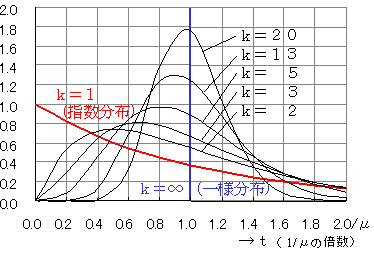
平均 = k/λ;　　分散 = k/λ2;
アーラン分布は、指数分布と一様分布の中間的な分布。
ｋ＝１なら指数分布、ｋ＝大なら正規分布、ｋ＝∞なら一様分布
　　p = (λ*t)k-1/(k-1)! * λe(-λ*t)
　　s = 区間 t=0～t の累積確率

t= λ= k=
p= s= 平均= 分散=
(→平均,分散)　 (t→p)　 (t→s)

ポアソン分布
　　平均分散：[平均, 分散] = distPoissonMV(λ);
　　確率密度： p = distPoissonDen(x,λ);
　　累積確率： s = distPoissonCum(x,λ);
　　累積確率の逆関数 x = distPoissonInv(s,λ);

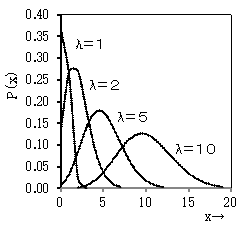
平均 = λ;　　分散 = λ2;
一定（微小）時間内にある事象が発生する回数が平均λであるとき、発生回数がｘとなる確率ｐは、
　　　　p(x) = (λx/x!)*e-λ　← distPoissonDen(x,λ)
　のポアソン分布に従う。
　（参照：「ポアソン分布と指数分布」、「離散型統計分布」
累積確率は、単純に s(x) = s(x-1) + p(x) で求めた。
逆関数は、x=0, 1, 2, ... として累積確率 s(x) を計算し、s(x) ≦ p である最大のｘを戻している。
　すなわち「確率ｐでｘ回以下だといえる」こととした。

λ=
x= p= s= 平均= 分散=
(→平均,分散)　 (x→p)　 (x→s)　 (s→p)

作表

作表１：λを固定し、ｘを0, 1, 2, ... と変化させたときの p と s を求める
作表２：λを固定し、ｐを変化させたときの ｘ を求める


 　　　

成長曲線

シグモイド関数
　　微分方程式　d = distSigmoidDen(x, c);
　　シグモイド関数　y = distSigmoidCum(x, c);
　　シグモイド関数の逆関数　x = distSigmoidInv(y, c);

　　c は正のスカラーです。
　　x, y, d は、右辺をスカラーに与えればスカラー、ベクトルならベクトルを戻します。

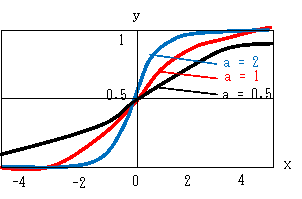
シグモイド関数とは、時刻 x における普及率 y の関係は、微分方程式
　　dy/dx = c * y * (1-y)　　　cは定数
で表される関数であり。その解は
　　y = 1/(1+e-cx)
になります。
シグモイド関数は右図のようになります。次の特徴があります。
・原点(0,0.5) に対して対称
・ｘ→-∞のとき ｙ→0. ｘ→∞のとき ｙ→1.　　いつかは全体に普及する。
・定数 c が大になると傾きが大になる。　短時間で y≒1 に達する
参照：「シグモイド関数」

d = distSigmoidDen(x, c)

定数 c が与えられたとき、時刻 x における微分係数 d を、次式により求めます。
　　d = c*y*(1-y) = c*(1-1/(1+e-cx))*(1/(1+e-cx))

入力
　var x = 1;　　// スカラー
　var c = 0.5;
　var d = distSigmoidDen(x, c);
出力
d = 0.118

y = distSigmoidCum(x, c)

定数 c が与えられたとき、時刻 x におけるシグモイド関数の値を求めます。
　　y = 1/(1+e-cx)

入力
　var x = [-1, 0. 1]; // ベクトル
　var c = 0.5;
　var y = distSigmoidCum(x, c);
出力
　y[0] = 0.378, y[1] = 0.5 y[2] = 0.622　// ベクトル

x = distSigmoidInv(y, c)

定数 c が与えられたとき、シグモイド関数の値 y に相当する x の値を、
distSigmoidCum　の逆関数
　　x = (1/c)log(y/(1-y))
で求めます。

入力
　var y = 0.9; // スカラー
　var c = 0.5;
　var x = distSigmoidInv(y, c);
出力
　x = 4.394

ケース２

c=
x= （y→x）
y= （x→y）
d= （x→d）

ロジスティック曲線（Logistic curve）
　　微分方程式　d = distLogisticDen(x, k, b, c)　
　　ロジスティック関数　y = distLogisticCum(x, k, b, c);
　　ロジスティック関数の逆関数　x = distLogisticInv(y, k, b, c);

　　k, b, c は正のスカラーです。
　　x, y, d は、右辺をスカラーに与えればスカラー、ベクトルならベクトルを戻します。


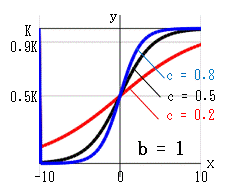
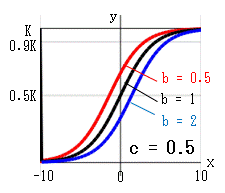
ロジスティック関数は、シグモイド関数を汎用化した関数です。
時刻 x における普及率 y の関係は、微分方程式
　　dy/dx = (c/k)*y*(k-y)　　　c,kは定数
で表される関数です。k=1 とするとシグモイド関数の微分方程式と一致します。
その解は
　　y = k/(1+b*e-cx)
になります。
シグモイド関数での y の存在範囲は 0～1 ですが、ロジスティック関数では 0～k になります。
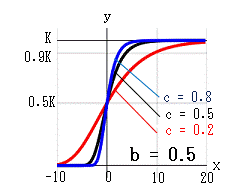
c の影響（右上図）
　K=1,b=1 とすると、シグモイド関数と一致します。
　c は傾き、c が大だと早く上限に達します。
ｂの影響（右下図）
　x=0 のときの状態を変化させます。
　ｂ=0 では y=k、b=∞ では y=0 になります。
参照：「ロジスティック曲線」

d = distLogisticDen(x, k, b, c)

定数 k,b,c が与えられたとき、時刻 x における微分係数 d を、次式により求めます。
　　d = (c/k)*y*(k-y)

入力
var x = [-1, 0, 1]; // ベクトル]
var k = 2;
　　var b = 0.5: // y を計算するために必要
var c = 0.5;
var d = distLogisticDen(x, k, b, c);
出力
d[0] = 0.248, d[1] = 0.222, d[1] = 0.179

y = distLogisticCum(x, k, b, c)

定数 k,b,c が与えられたとき、時刻 x におけるロジスティック関数 y を、次式により求めます。
　　y = k/(1+b*e-cx)

入力
var x = [-2, 0, 2, 5, 10];
var k = 2;
var b = 0.5;
var c = 0.5;
var y = distLogisticCum(x, k, b, c);
出力
y[0] = 0.848, y[1] = 1.333, y[2] = 1.689, y[3] = 1.921, y[4] = 1.993

x = distLogisticInv(y, k, b, c);

定数 k,b,c が与えられたとき、ロジスティック関数 y となる時刻 x を次式により求めます。
　　x = -(1/c)log((k-y)/(b*y))

実務対応
ロジスティック関数では、折返点が x=0 になっています。しかし実務では最初に観測した点を t=0 とするのが通常であり、そのときの y0 の値は既知のはずです。
　　x0 = -(1/c)log((k-y0)/(b*y0))
を計算して、t = x + x0 とすることで解決します。

入力
var y = [0.5, 1, 1.9, 1.99];
var k = 2;
var b = 0.5;
var c = 0.5;
var x = distLogisticInv(y, k, b, c);
出力
x[0] = -3.583, x[1] = -1.386, x[2] = 4.503, x[3] = 9.200,


ケース２

k= b= c=
x=
y=
d=

ゴンペルツ曲線（Gompertz curve）
　　微分方程式　d = distGompertzDen(x, k, b, c]);
　　ゴンペルツ関数　y = distGompertzCum(x, k, b, c);
　　ゴンペルツ関数の逆関数　x = distGompertzInv(y, k, b, c);


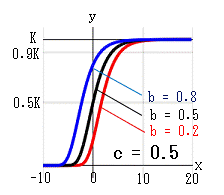
ゴンペルツ曲線は、成長の変化 dy/dx を
　　・現在の個数に比例して増大する
　　・時間が経過するのに伴い指数的に減少する
の積として捉えます。
　　　dy/dx = A*y*e-cx　　A。ｃは定数
これを　－∞ ～ x まで累積した曲線がゴンペルツ曲線です。（A = -c*log(b)と変形）
　　y = Kbｅ-cx　　k.b,c は定数
ゴンペルツ曲線は、次の特徴があります。
　　ｘ→∞ のとき：ｅ－ｃｘ→０、ｂ0＝１、ｙ→Ｋ
　　ｘ→－∞のとき：ｅ－ｃｘ→∞、ｙ→ｂ∞→０
　　ｘ＝０ のとき：ｅ－ｃｘ＝１、ｙ＝Ｋｂ
　b, c を変化させたときの曲線の変化を示します。
　　 b：x=0 のときの y を y0 とすれば、y0 = Kb になります。
　　　　c：曲線の傾きを示します。 ｃ→大 になると傾きが大になります。
　　　　x = 0 は曲線の変曲点でもあります。
　ｂ→小、ｃ→小 になると、Ｋ値に近ずくまでの時間 ｘ が長くなります。
参照：「ゴンペルツ曲線」

d = distGompertzDen(x, k, b, c])

時刻 x におけるゴンペルツ曲線の微分係数（個体数の増減）を求めます。
　　　dy/dx = d = -c*log(b)*y*e-cx

入力
　　var x = [-2, 0, 2, 10]; // ベクトル]
　　var k = 2;
　　var b = 0.5;
　　var c = 0.5;
　　var d = distGompertzDen(x, k, b, c);
出力
　　d[0] = 0.286, d[1] = 0.347,,d[2] = 0.198, d[3]=0.005

y = distGompertzCum(x, k, b, c);

時刻 x におけるゴンペルツツ関数 y の値
　　y = Kbｅ-cx

入力
　　var x = [-2, 0, 2, 5, 10];
　　var k = 2;
　　var b = 0.5;
　　var c = 0.5;
　　var y = distGompertzCum(x, k, b, c);
　出力
　　y[0] = 0.3034 y[1] = 1.000, y[2] = 1.550. y[4] = 1.889, y[4] = 1.991/p>

x = distGompertzInv(y, k, b, c);

ゴンペルツツ関数の値が y となる時刻 x
　　x = -(1/c)log(log(k/y)/|log(b)|)

実務対応
ゴンペルツツ関数では、折返点が x=0 になっています。しかし実務では最初に観測した点を t=0 とするのが通常であり、そのときの y0 の値は既知のはずです。
　　x0 = -(1/c)log(log(k/y0)/|log(b)|)
を計算して、t = x + x0 とすることで解決します。

入力 　　var y = [0.5, 1, 1.9, 1.99];
　　var k = 2;
　　var b = 0.5;
　　var c = 0.5;
　　var x = distGompertzInv(y, k, b, c);
出力
　　x[0] = -1.386, x[1] = 0, x[2] = 5.207, x[3] = 9.858


ケース２

k= b= c=
x=
y=
d=

オッズ、ロジット（シグモイド曲線関連）
　　オッズ　　Odss = distOdss(p)　
　　ロジット　Logit = distLogit(p)　

　　p は 0～1 で、スカラーでもベクトルでも構いません。それに応じて、
　　x, y, d は、右辺をスカラーに与えればスカラー、ベクトルならベクトルを戻します。

オッズ（odds）
オッズとは、ある事象 x が起こる可能性を示すもので、発生確率を p (0≦p≦1）とすると
　　オッズ = 発生しない確率／発生する確率 = p/(1-p)
で定義されます。
　　０≦オッズ＜１　　発生する確率 ＜ 発生しない確率
　　　　オッズ＝１　　発生する確率 ＝ 発生しない確率
　　１＜オッズ＜∞　　発生する確率 ＞ 発生しない確率
ロジット（Log Odds = Logit）
ロジットとは、オッズの対数をとったものです。
　　ロジット = log(p/(1-p))
で定義されます。
　 －∞＜ロジット＜０　　０ ＜ p ＜ ０.５
　 　　　ロジット＝０　　　　　 p ＝ ０.５
　　　０≦ロジット＜∞　　０.５＜ p ＜ １

ロジットとシグモイド関数の関係

シグモイド関数 y = 1/(1+e-cx で c=1 とした y = 1/(1+e-x) を標準シグモイド関数といいます。その逆関数は x = log(y/(1-y)) になります。
ここで、y は、時刻 x における発生確率だといえmす。それで x→t、y→p と書き直すと、
　　 t = log(p/(1-p)) = ロジット
になります。
参照：「ロジスティック回帰分析の前提概念」

ケース１

　　var Odss = distOdss(0.6); // スカラー
　　　　// Odss = 1.5
　　var Logit = distLogit([0.6, 0.8]); // ベクトル
　　　　// Logit[0] = 0.405, Logiit[1] = 1.386

ケース2

p　　=
Odss =
Logit=

オッズ比　OR = distOdssRatio(n00, n01, n10, n11)　

下表の n00, n01, n10, n11 を与えて、OdssRatio を計算します。
　　　　　事象あり　事象なし　 合計 p オッズ
　　群Ａ　　 n00 n01　　 s0=n00+n01 p0=n00/s0　　Odss0=p0/(1-p0)
　　群Ｂ n10 n11　　 s1=n10+n11 p1=n10/s1 Odss1=p1/(1-p1)
　　　オッズ比　OddsRatio = Odss0/Odds1 　　var OdssRatio = distOdssRatio(n00, n01, n10, n11);

具体例
　喫煙と肺がんの関係で、次のデータがあるとします。
　　　　　　　　　喫煙者　非喫煙者　　合計　 肺がん確率
　　肺がんの人　　　４０　　１０　　　５０　p0 = 40/50 = 0.8
　　健康な人　　　　２０　　８０　　１００ p1 = 20/100 = 0.2
　オッズ比 = (p0/(1-p0)) / (p1/(1-p1)) = (0.8/0.2)/(0.2/0.8) = 16
　→健康な人と比べて、肺がんの人では喫煙者が肺がんである可能性が非喫煙者の１６倍になる。

n00= n01= 　　s0= p0= Odss0=
n10= n11= 　　s1= p1= Odss1=
OdssRatio =