多変量解析とは、互いに関連した複数個の観測項目のデータ(多変量データ)から,項目間の関係を検討するための統計的手法です。ここでは、数学的な分野は一切割愛して、代表的な多変量解析手法を列挙して、その特徴を示すだけにします。
| 目的 | 被説明変数 目的変数 | 説明変数=量的 | 説明変数=質的 |
| 予測 | 量的 | 重回帰分析 | 数量化1類 |
| 予測 | 質的 | 判別分析 | 数量化2類 ロジスティック回帰 |
| 分類 | なし | 主成分分析 因子分析 | 数量化3類 |
AIとの関係
多変量解析は統計的手法の一分野ですが、AIではこれらの手法を「ルールベースAI」(全てのルールを人間が与える)として、AIの一分野に位置づけています。
●機械学習での区分
- 教師あり学習(被説明変数あり)
AIでは、被説明変数のことをラベルといい。教師が与える正解だとしています。ラベル付きデータを大量にAIに与えて、それからAIがルールを作る(例えば判別式を作成する)ことになります。
・回帰()≒重回帰分析、分散分析
・分類(classficication)≒判別分析、ロジスティック回帰分析 - 教師なし学習(被説明変数なし)
・クラスタリング(clustering)≒主成分分析、階層型クラスタリング
・次元削減(dimensionality reduction)≒因子分析
回帰分析
重回帰分析

たとえば、店舗の売上高yを店舗面積x1、地価x2、店員数x3などから、
y=a0+a1x1+a2x2+a3x3
として、最小自乗法などによりa0、a1、a2、a3を算出して、新規店舗の売上高を予測したり、既存店舗の実績売上高との比較をしたりします。
●数値例
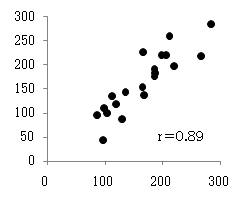
例えば、右図のように、y、x1、x2、x3のデータが与えられたとき、単にそれぞれのxとyがどのように関係しているかを調べたのでは、次の散布図になり、その関係はあいまいです。相関もあまり大きくありません(x3はかなり大きいですが)。

最小自乗法により、次の式が得られます。
y=-153.3+2.408x1+0.401x2+9.336x3 ・・・A
これに個々のデータを代入すると、右図の計算値になります。これとyとの相関係数は0.89になり、かなりの説明力があることがわかります。
●留意点
以降の事項は、多変量解析に共通する留意点です。
- どうして、x3単独のときとくらべて、相関が大きくなったのでしょうか?
単純にいえば(x1、x2、x3)が組になっているという情報が加わったからです。このように、個別の要因をばらばらに分析するよりも、全体で考えることが重要なのです。これが、多変量解析を行うことのメリットなのです。 - しかし、説明変数の個数を増やせばよいとはいえません。
たしかに、説明変数の個数を増やせば、実際の値と計算値は近くなり、相関係数は大になります。しかしそれは見掛け上の改善にすぎません。説明は省略しますが、説明変数が多くなると、データが少し変化するだけで、計算式が大きく変化してしまうのです。すなわち、計算式が不安定なので、予測の信頼性が低くなるのです。むしろ、相関係数はある程度小さくても、説明変数が少ないほうが、適切なことが多いのです。 - 説明変数の採用・不採用には、実務的な知識が重要です。
例えば、x1を削除すると、計算式は、
y=8.68+0.577x2+6.484x3 ・・・B
となり、相関係数は0.73になります。
数学的には、Aのほうが相関係数が大なので適切だといえるかもしれませんが、実務の面でとらえると、定数項や係数の値はむしろBのほうが適切だということがあるかもしれません。多変量解析はあくまでも実務の道具です。これらを総合的に判断することが重要なのです。
分散分析
分布。検定、信頼区間など、多変量解析の代表的手法ですが、分量が多いので、別章「分散分析」にしました。
分類
ロジスティック回帰
ロジスティック回帰は、説明変数が量的でも質的でもよく、被説明変数は0/1の2値データです。数量化2類の判別分析に似ていますが、判別分析では判別式により、0/1のどちらに属するかを求めるのに対して、ロジスティック回帰は、被説明変数が事象発生確率になります。
例えば、喫煙本数(量的データ)、辛いもの好き(質的データ)、胃潰瘍病歴の有無(質的データ)などの説明変数とガンの発生確率の関係を調べようとする分析技法です。

質的データを0/1にすれば、重回帰分析や判別分析と同様な処理により回帰式を求めることができます。判別分析では回帰式の値によりどちらのグループに属するかを判別しますが、それを実現確率とするには、値が0~1の範囲になるように変換する必要があります。その変換に「 ロジスティック曲線」(その一種であるシグモイド曲線など)を用います。
実際に適切な分析をするには、回帰式作成での工夫、ロジスティック曲線の選択の工夫などが必要ですが、高度な知識を必要とするので、ここでは省略します。また、実際の計算例や機械学習の例は「 ロジスティック回帰」にあります。
ロジスティック回帰では発生確率 y のことをオッズ(odds)といいます。1-y は発生しない確率になりますが、その比 y/(1-y) をオッズ比といいます。
この確率発生計算式があれば、新しい説明変数のデータが発生したとき発生確率を計算できます。これをロジスティック予測といいます。
判別分析
判別関数とは、重回帰分析での目的関数が「合格/不合格」などの質的な値になるものです。
合格、不合格になる判定基準は不明です。主な要因がx1、x2であろうと推察されますが、それ以外にあるかもしれません。そのような場合に、x1、x2から計算した値yが
y≧α なら合格
y<α なら不合格
としているのではないかと考えて、その計算式
y=a0+a1x1+a2x2
を探そうとする方法です。それによって得られた式を判別関数といいます。
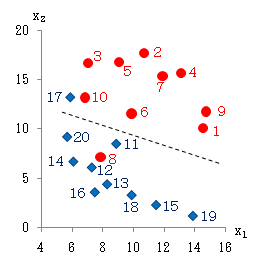
例えば、右図のように、合格になった(y=1)事例と、不合格になった(y=-1)事例のデータ(x1,x2)があるとします。その散布図は下図のようになります(赤:y=1、青:y=-1)。このとき、赤と青を分離する点線のような判別関数をみつけようとするものです。
●重回帰分析による判別式の算出
上のように、合格をy=1、不合格をy=-1として重回帰分析を行えば、合格ならyは1に近くなるし、不合格なら-1に近くなるはずです。重回帰の式は
y=-2.455+0.1058x1+0.1468x2
となりました。
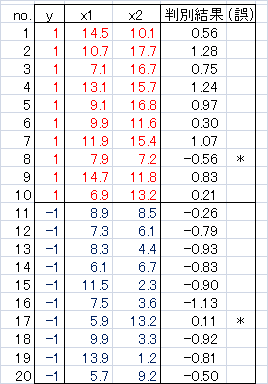
これに、各データのx1とx2を代入したのが「判別結果」です。
そしてここでは、合格・不合格の判定値αを0としました。すなわち、y≧0になれば合格、y<0ならば不合格としているのだろうと考えました。
その結果、No.8とNo.17で判定誤りがありましたが、全体としてはかなりよい判別関数であるといえます。
●マハラノビスの距離
もっと高度な理論(その内容は省略。用語だけの紹介)では、合格・不合格の2つのグループを曲線で分割する方法があります。変数がひとつの場合に、どれだけ散らばっているかを示す尺度が分散σ2ですが、変数が複数の場合には、相関を考慮した距離であるマハラノビスの距離D2という尺度があり、それを用いて判別しようとする方法です。
クラスタ分析(クラスタリング)
クラスタリングとは、「似たものあつめ」です。例えば、右図のように、x1~x4の因子から、いくつかのグループに分類するようなときに用います。
クラスタリングは、二つの方法があります。
非階層型クラスタリング=主成分分析、K-means法
階層型クラスタリング=ウオード法
主成分分析
重回帰分析や判別分析では、目的変数がありますが、主成分分析では目的変数はありません。主成分分析は、いくつかの要因を合成(圧縮)して、少ない成分を探しだし、いくつかのグループに分類することを目的にしています。
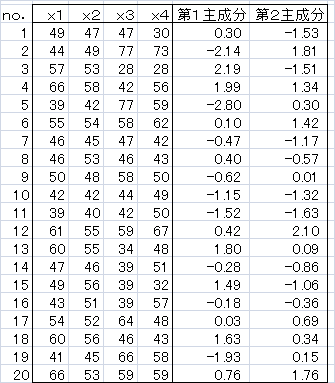
例えば、右図のような数学・理科・国語・英語などの成績データから、一つあるいは二つの成分を取り出すことにより、生徒をいくつかのグループに分類するようなときに用います。
この理論は、分散共分散行列や固有値など高度な数学を用いますので、ここではイメージ的な説明にとどめます(したがって、厳密な説明ではありません)。
データの重心を通り、各点からの距離が最小になるような直線(最小自乗法をイメージ)を考えます。それを第1主成分とします。次に、第1主成分の要素を取り除いたデータを用いて同様なことを行い、第2主成分とします。
ここでのデータを用いると、
第1主成分:z1=0.56x1+0.58x2-0.48x3-0.35x4
第2主成分:z2=0.43x1+0.39x2+0.50x3+0.62x4
が得られます。
各データについて、z1とz2を計算すると、下の散布図が得られます。
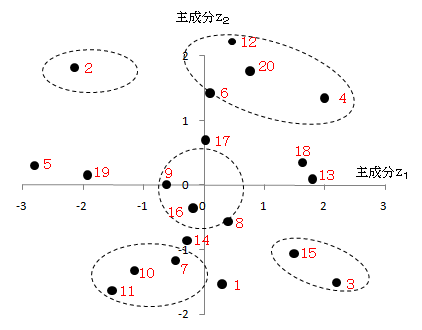
x1が数学、x2が理科、x3が国語、x4が英語の成績であり、第2主成分z2の係数がすべて正であることから、これは総合能力を示していると考えられます。また、第1主成分z1は、数学と理科の係数が正、国語と英語の係数が負であることから、理系・文系、あるいは分析力・語学力の能力であると考えられます。
そして、生徒4や20などは、理系で総合的によくできる生徒群、生徒11や10は、文系であまり成績がよくない生徒群というように分類できます。
また、原点(0,0)に近い生徒16や9は、生徒全体で一般的なグループに属するといえます。
ここで重要なのは、これら主成分の実務的な意味は、これらの計算過程で示されるのではなく、主成分の式(係数)や散布図から分析者が主観により意味づけをすることです。ですから、本当に総合能力や理系・文系であるかどうかではなく、分析者がそのように分析したということなのです。
K-means法
代表的な非階層クラスタリングのライブラリです。PythonやRのアドオンとして、AIの分野では「主成分分析」よりも「K-means法」の用語のほうが広く使われています。
階層型クラスタリング
例題
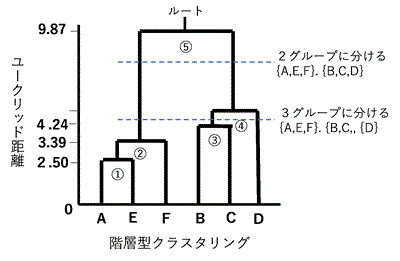
下表のように、生徒の科目別成績表があります。これから「似た者集め」をして、右図(デンドログラムという)を作成します。
生徒 国語 数学 理科 社会 英語
A 3 10 9 4 9
B 7 4 4 8 10
C 10 6 5 10 10
D 9 5 2 7 6
E 2 10 10 4 7
F 5 8 9 3 8
計算方法
AとBの間のユークリッド距離√{(3-7)2+(3-7)2+…+(9-10)2} = 9.70
同様にAとC~E 間の距離を計算する。
A B C D E
B 9.70
C 10.86 4.24
D 11.31 5.10 6.00
E 2.45 11.05 12.24 12.17
F 3.16 8.60 9.90 9.70 4.00
① この中で最小(最も似ている)なのは A-E →A,Eを一つにまとめる。
結合した後の値は平均値とする。
AE 2.5 10 9,5 4 8
B 7 4 4 8 10
C 10 6 5 10 10
D 9 5 2 7 6
F 5 8 9 3 8
AEと他間の距離
AE B C D
B 10.32 灰色部分は前と同じ
C 11.51 4.24
D 11.66 5.10 6.00
F 3.39 8.60 9.90 9.70 ② 最小値はAE-F なので、AEF を結合する。
AEF B C
B 9.35
C 10.60 4.24
D 10.60 5.10 6.00
③ BとCを結合する。
AEF BC
BC 9.77
D 10.60 5.14
④ BCとDを結合する。
AEF
BCD 9.86
⑤ ここで全ての生徒が、いづれかのグループに入り、ルートノードに接続したので終了する。

●計算結果
結合 距離 未帰属
① AE 2.50 B,C,D.F
② AEF 3.39 B,C,D
③ BC 4.24 D
④ BCD 5.14
⑤ AFE,BCD 9.87
これを図示すると右のデンドログラムになります。
「距離」と郡内代表値
階層型クラスタリングでは、「距離」が需要な尺度です。そのため、いろいろな「距離」があります、
距離一般
・ユークリッド距離:分散の平方。本章で示した距離で、最も一般的
・マンハッタン距離:差の絶対値。単純で大量計算での効率はよいが、信頼性が低い
・マハラノビス距離:分散共分散行列の逆行列を使う。異常値の検知に有効
群内代表値(クラスタ間距離に用いるクラスタ位置)
・重心法。サンプルの平均を使う。本章はこれを使った。
・最短距離法、最長距離法:最も距離が短い(長い)ものをクラスター間の距離とする。
計算量が少ないが、外れ値に弱い
・群平均法。
●ウォード法 結合後の位置と結合前の位置の差の二乗和を用いる、
分類感度が高くAIでは代表的方法になっている。
因子分析
例えば、多数の生徒の英語・数学・国語・理科・社会の成績から、それらの教科間の相関を計算すると、次の結果が得られたとします。
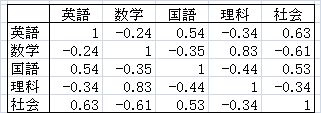
数学と理科との相関係数は0.83なので、数学と理科は似たような能力を示しているといえます。数学と社会の相関係数は-0.61なので、数学と社会では、相反する能力であるといえます。また、数学と英語の相関係数は絶対値が小さいので、両科目の間の関係は小さいといえます。
すなわち、これら5つの教科の示す能力は、もっと少ない説明要因(これを因子という)で説明できると考えられます。因子分析とは、その因子を探すための方法です。5教科を分類すること、それにより、生徒を分類する方法だともいえます。
因子分析も主成分分析と同様に、目的変数をもたず分類を行う方法ですが、両者の間には大きな違いがあります。主成分分析では主成分が結果として得られたのですが、因子分析では因子を説明変数としているのです。
英語や数学などの教科を変数x、因子をf、誤差(独立因子という)をeとして、
x1=a11f1+a12f2+・・・+e1
x2=a21f1+a22f2+・・・+e2
:
xn=an1f1+an2f2+・・・+en
において、誤差の2乗和が最小になるようなaijを求めます。このaijを因子負荷量といいます。
主成分分析では、誤差を無視しているのに対して、因子分析では誤差を独立因子として分析の対象にしていることも特徴の一つです。
計算プロセスは省略して、次の結果が得られたとします。
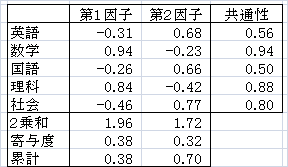
- 因子負荷量
- 上のaijですが、独自因子(誤差)の分を除いた各変数と各因子の相関を表わしています。
第1因子では、数学や理科が正で大きく社会や国語は負になっていることから理系能力、第2因子では、社会や英語が正で大きく、数学や理科が負になっていることから文系能力というように、実務的な主観により名前をつけます(これは主成分分析と同じです)。 - 共通性
- 因子負荷量の2乗を横に合計したものです。各変数が因子群によってどれだけ説明できるかの尺度になります。この例では、この2つの因子により、数学や理科については非常によく説明できるが、英語についてはあまり説明できていません。
- 寄与率
- 因子負荷量の2乗を縦に合計したものを用いて、その因子で全体のどれだけを説明できたかを示します。この値が1に近ければ説明力が高いことになります。ここでは、第1因子だけで0.38、第1因子と第2因子で0.70を説明していることになります。
因子分析では、主成分分析と同様に固有値の計算が必要になるだけでなく、少ない因子で寄与率が高くなる因子負荷量を求めるために、軸の回転という複雑な計算が行われます。
数量化理論
ここまでは、説明変数として売場面積や数学の成績など「量」的な変数を対象にしてきました。ところが、実務での分析では、立地条件(商業地域か、住宅地域か)とか官能判断(甘い、辛い、酸っぱい)など「質」的な変数を取り扱う必要があります。質的変数では大小関係がないものや、大小関係があっても、1と2の差が2と3の差と異なるものがあります。このような変数も取り扱えるように拡張したのが数量化理論です。
数量化1類: 重回帰分析
数量化2類: 判別分析
数量化3類: 主成分分析、因子分析
などが広く用いられています。