一様分布
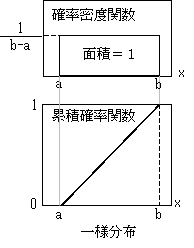
| x<a | a≦x≦b | b<x | |
| 確率密度関数 | 0 | 1 b-a |
0 |
| 累積確率関数 | 0 | x-a b-a |
1 |
平均:(a+b)/2
分散:(b-a)2/12
一様分布の価値
一見、一様分布はつまらない分布のようですが、0~1の一様分布に従う乱数発生関数 random() は、多くのプログラミング言語で標準装備されており、これから多様な分布に従う乱数が生成できるのです。
- 正規乱数の生成
標本数を多くすると、多様な分布が正規分布に近ずくという中心極限定理があります。random() で発生させた12個の乱数の和は、平均6、分散1の正規乱数になります。 - 三角乱数の生成
二つの random() の和は、0~2、最頻値1の三角乱数になります。また、二つのrandom() の小さいほうを選んだものは、0~1、最頻値0の三角乱数になります。
三角分布

| x<a | a≦x<c | x=c | c<x≦b | b<x | |
| 確率密度関数 | 0 | 2(x-a) (b-a)(c-a) |
2 b-a |
2(b-x) (b-a)(b-c) |
0 |
| 累積確率関数 | 0 | (x-a)2 (b-a)(c-a) |
c-a b-a |
1- 2(b-x)2 (b-a)(b-c) |
1 |
平均:(a+b+c)/3
分散:(a2+b2+c2-ab-bc-ca)/18
 型(c=b)
型(c=b)
| x<a | a≦x<b | x=b | b<x | |
| 確率密度関数 | 0 | 2(x-a) (b-a)2 |
2 b-a |
0 |
| 累積確率関数 | 0 | (x-a)2 (b-a)2 |
1 | 1 |
平均:(a+2b)/3
分散:(a2+b2-3ab)/18
 型(c=a)
型(c=a)
| x<a | x=a | a<x<b | b≦x | |
| 確率密度関数 | 0 | 2 (b-a) |
2(b-x) (b-a)2 |
0 |
| 累積確率関数 | 0 | 0 | 1- (b-x)2 (b-a)2 |
1 |
平均:(2a+b)/3
分散:(b-a)2/18
三角分布は、直観的にパラメタを設定できますし、その形状から、多様な分布を近似できます。そのため、精度を重視しない用途では計算量を減らすために代用することが多くあります。