論理回路
論理回路とは、論理演算を行う電子回路です。真理値の「真/偽」、2進法の「0/1」、電気の「ON/OFF」のように2つの状態をもちます。コンピュータは、多数の記憶素子と多数の論理回路を複雑に組み合わせたものだといえます。
論理回路は、次の2つに大別されます。
- 組み合わせ回路
現在の入力のみで出力が決まる回路。ゲートともいう。AND、OR、XORなど - 順序回路
過去の内部状態と取得時の入力信号とで出力が決まる回路。フリップフロップ、レジスタなど。
組み合わせ回路一覧
| 名称 | ベン図 | 真理値表 | 論理回路 | 名称 | ベン図 | 真理値表 | 論理回路 | |
|---|---|---|---|---|---|---|---|---|
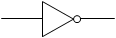
| 否定 NOT |
 |
A X |
 | |||||
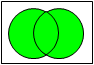
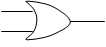
| 論理和 OR + |
 |
A B X |
 |
否定論理和 NOR |
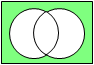 |
A B X |
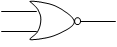 |
|
| 論理積 AND × |
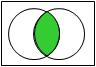 |
A B X |
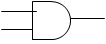 |
否定論理積 NAND |
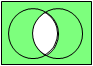 |
A B X |
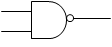 |
|
| 排他的論理和 XOR EOR 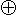 |
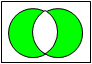 |
A B X |
 |
等価演算 一致演算 IFF |
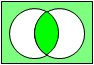 |
A B X |
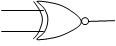 |
AとB AND XOR OR NOR IFF NAND
共に0 0 0 0 1 1 1
一方1 0 1 1 0 0 1
共に1 1 0 1 0 1 0
ビット演算
二つの2進数(ここでは8ビットとします)に、各ビットで論理和や論理積をすることをビット演算といいます。任意の2進数Xに、00001111=0F16(Y)をビット演算します。このとき規則的なビット列Yをマスクといいます。
ここでは、X=01010101とします。
論理和(OR):1を与えたビットをすべて1にする
0101 0101
OR) 0000 1111
0101 1111
└──┘ └──┘
元のまま すべて1
論理積(AND):0を与えたビットをすべて1にする
0101 0101
AND) 0000 1111
0000 0101
└──┘ └──┘
すべて0 元のまま
排他的論理和(XOR):1を与えたビットを反転
0101 0101
XOR) 0000 1111
0101 1010
└──┘ └──┘
元のまま 反転
否定論理積(NAND):0を与えたビットをすべて1、1を与えたビットを反転
0101 0101
NAND)0000 1111
1111 1010
└──┘ └──┘
すべて1 反転
多数ビットの排他的論理和:
Pn=b1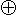 b2
b2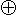 …
…  bn
bn
=1 (1のビットの個数が奇数のとき)
=0 (1のビットの個数が偶数のとき)
→パリティチェックに利用される
(証明)。
数学的帰納法で考える。
n=1のとき、
P1=b1 であるから、
1のビットの個数が奇数(1個)ならば1
1のビットの個数が偶数(0個)ならば0
で正しい。
n>1のとき、n-1まで正しいとすれば、
Pn=Pn-1 bn であり、
bn であり、
Pn-1=1、bn=1 ならば Pn=0
b1~bn-1 までで1のビット数が奇数で bnが1ならば全体で偶数
以下、同様に検討すれば、正しいことがわかる。
半加算器と全加算器
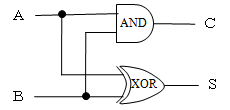
1ビットの数AとBを加算して、その結果を1ビットの数Sに入れ、繰り上がり(キャリーという)を1ビットの数Cに入れる回路を半加算器といいます。
入力 出力
A B S C
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
となるので、SはXOR回路、CはAND回路で実現することができます。
下位の桁からの繰り上げを取り込んだ加算回路を全加算器といいます。全加算器は、半加算器を2つ用いて構成します。

入力 中 間 出力 単純計算
C A B S1 C1 S2 C2 S C C+A+B
0 0 0 0 0 0 0 0 0 0
0 0 1 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1 0 1
0 1 1 0 1 0 0 0 1 10
1 0 0 0 0 1 0 1 0 1
1 0 1 1 0 0 1 0 1 10
1 1 0 1 0 0 1 0 1 10
1 1 1 0 1 1 0 1 1 11
フリップフロップ回路
過去の信号を記憶しておき、新規の信号が与えられると、その関係によって信号を出力する回路を順序回路といいます。その代表的なものが、フリップフロップ回路です(その語源?)。フリップフロップ回路は1ビットの信号を記憶でき、高速に入出力できるので、高速な記憶素子であるSRAMに用いられています。
フリップフロップとは、シーソーの「ギッタンバッタン」の擬音からだそうだ。上がりっぱなし、下がりっぱなし、上がったり下がったりすることからであろう。そのためか、ON(1)/OFF(0)の状態をHigh/Lowで示す人もいる。
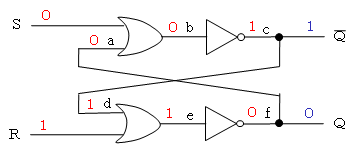
フリップフロップ回路には多様な回路がありますが、単純な回路は「SR-フリップフロップ回路」で、OR回路とNOT回路を組み合わせたものです。
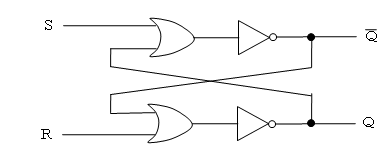
現在の状況をQ(その否定をQ)とします。そして、セット信号S、リセット信号Rを与えたとき、その結果として出力されるQおよびQは、次のようになります。
S=0、R=0:現在の状況がそのまま保持される(Q、Qは変化しない)
S=1、R=0:Q=1(Q=0)にセットされる
S=0、R=1:Q=0(Q=1)にリセットされる
S=1、R=1:セットとリセットを同時に行うことはないとする
- 何もしないとき(S=0、R=0)
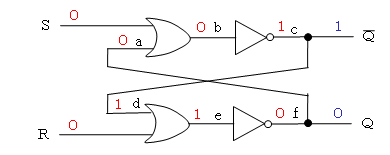
現在の状態が、Q=0(Q=1)であったとします。
Q=0なので、a=0になります。
bは、[S or a] なのでb=0、cはbの否定なのでc=1となります。
すなわち、出力されるQ(=c=1)は、現在と変わりません。
また、c=1から、d=1、e=[R or d]=1、f=0となり、出力されるQも変化しません。
すなわち、現在の状況が保持されます。
同様にして、Q=1(Q=0)の場合も、現在の状況が保持されます。- セットするとき(S=1、R=0)
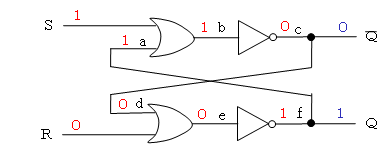
現在の状態が、Q=1(Q=0)であったとします。
Q=1なので、a=1、b=[S or a]=1、c=0、Q=c=0
c=0から、d=0、e=[R or d]=0、f=1となり、Q=1になります。
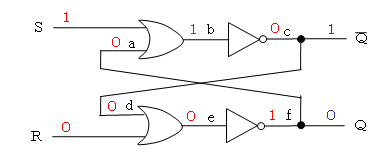
現在の状態が、Q=0(Q=1)であったとします。
Q=0なので、a=0、b=[S or a]=1、c=0、Q=c=0
すなわち、Qが1から0に変化しました。
そして、c=0から、d=0、e=[R or d]=0、f=1となり、Q=1に変化しました。
このように、Qがどのような状態であっても、S=1により、Q=1になります。- リセットするとき(S=0、R=1)
- このときも、セットのときと同様にして、現在のQがどのような状態であっても、Q=0になります。
そのときのa~fの値がどうなるかは、練習問題とします。
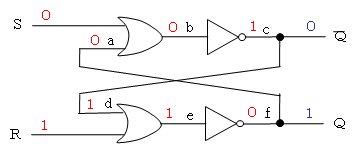
Q=0のとき