論理演算
1と0、真と偽、ON/OFFのように2つの状態だけをとることのできる数を論理数といい、論理数の間の演算を論理演算(プール代数ともいう)といいます。
論理演算を理解するには、図表が役に立ちます。代表的な図にベン図、表に真理値表があります。
論理演算子
- 否定
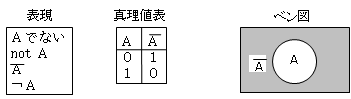
- 論理積
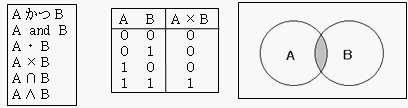
- 論理和
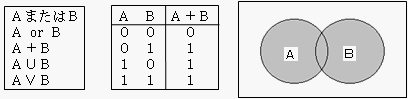
- 排他的論理和
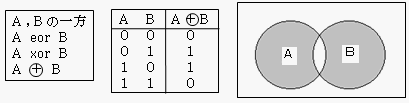
論理演算の基本公式
- AとAの演算
A×A=A
A+A=A
A×A=0
A+A=1
- 0,1との演算
A×0=0
A×1=A
A+0=A
A+1=1
- 交換則
-
A×B=B×A
A+B=B+A
- 結合則
-
(A×B)×C=A×(B×C)
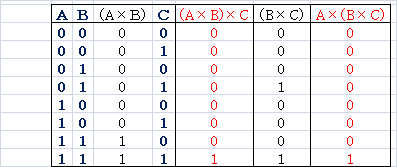
(A+B)+C=A+(B+C)
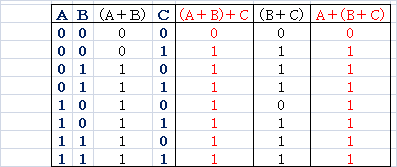
- 分配則
-
A×(B+C)=(A×B)+(A×C)
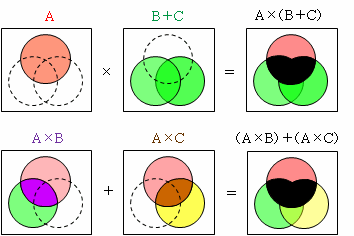
A+(B×C)=(A+B)×(A+C)
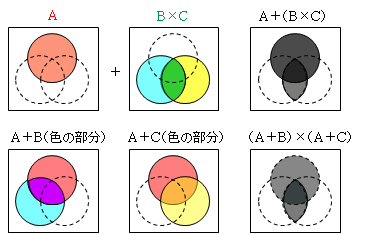
- 吸収則
-
A+(A×B)=A 証明:A+(A×B)=A×(1+B)=A×1=A
A×(A+B)=A 証明:A×(A+B)=A×A+A×B=A×(1+B)=A - ド・モルガンの公式
-
A×B=A+B
A+B=A×B

集合演算
- 1から10までの自然数の集まりのように,それに含まれる「もの」がはっきりしているような,「もの」の集まりを集合といいます。
- 集合を構成する要素 1、2,3、… のことを要素あるいは元といいます。
- 集合Aが1,2,3を元とする集合であることを X={1,2,3}と表記します。このように具体的に列挙する定義を外延的定義といいます。
- それに対して、内包的定義では、{a|a∈自然数 ∧ 1≦a≦3}と表記します。これは「aとは、 自然数であり、かつ、1≦a≦3である」という意味になります。
- 元が無限大の場合、例えばXはすべての自然数であるような場合は X∈自然数 と表記します。
- このときの「自然数」に相当する「対象とする全体」を全体集合といいUで表します。空間ということもあります。
- 元をもたない集合を空集合といい、φで表します。
| 関係 | 記号 | 意味 | 例示 |
|---|---|---|---|
| >恒等関係 | A=B | AとBは同じ元からなる | A={2,4}、B={2,4}のとき、 A=Bが成立する |
| 包含関係 | A⊂B | Aの全元はBに存在する AはBの部分集合である |
A={2,4}、B={1,2,3,4,5}のとき A⊂Bが成立する |
A⊂BとA=Bを合わせて、A⊆B と書きます。
論理演算と集合演算
論理演算での変数は論理変数で、Aは0と1の二値をとります。それでA+Aは「AあるいはAでない確率」であり1になります。
それに対して、集合演算での変数はリストで、A={2、6、4}のような任意の個数の要素を持ちます。それで対象とする空間が自然数だとすれば、A+Aは「AあるいはAでない自然数の集合」となります。
このような違いはありますが、「Aが1であり、かつ、Bが1である確率はA×B(理論積)」と「ある要素がAにあり、かつ、Bにもある要素はA∩B(積集合)」の対比や、どちらもAとBの順序を変えても等価であるとの交換則が成立するなど、共通する数学的方法が多くあります。
論理演算 集合演算
0 φ(空集合)
1 U(全体集合)
否定(A) 補集合(A)
論理和(+) 和集合(∪)
論理積(×) 積集合(∩)
の対応を知っていれば、集合演算の多くは論理演算での説明が使えます。
集合演算子
| 集合式 | 演算子 | 内包的定義 | 意味 | 例示 |
|---|---|---|---|---|
| 補集合 | A | U-A | Aに所属しない元 | U={1,2,3,4}、A={2,4}のとき A={1,3} |
| 和集合 | A∪B | {x|x∈A ∨ x∈B} |
少なくとも一方に所属する元 | A={1,2,3}、B={2,3,4}のとき A∪B={1,2,3,4} |
| 積集合 | A∩B | {x|x∈A ∧ x∈B} | AとBの両方に所属する元 | A={1,2,3}、B={2,3,4}のとき A∩B={2,3} |
| 差集合 | A-B | {x|x∈A ∧ ¬x∈B} | Aに所属しBに所属しない元 | A={1,2,3,4}、B={1,3,5}のとき A-B={2,4}、B-A={5} |
| 直積 | A×B | 直積 {(a,b)| a∈A ∧ b∈B} | Aの元とBの元の組み合わせ | A={1,2,3}、B={p,q}のとき A-B={(1,p),(2,p),(3,p),(1,q),(2,q),(3,q)} |
- 積集合と直積(カルテシアン積ともいう)は異なります。論理積の×の記号は、集合計算での∩に似た概念です。
- 差集合のとき、引く側だけにある元は無視されます。
集合演算の基本公式
- AとAの計算
- A∪A=A、 A∩A=A、 A-A=φ
A∪A=U、 A∩A=φ、 A-A=A - 空集合φとの計算
- A⊃φ、 A∩φ=φ、 A∪φ=A、 A-φ=A、 φ-A=φ、 A×φ=φ
- 全体集合Uとの計算
- U⊃A、 A∩U=A、 A∪U=U、 A-U=A、 U-A=A、
- 交換則
- A∪B⇔B∪A、 A∩B⇔B∩A
- 結合則
- (A∪B)∪C⇔A∪(B∪C)、 (A∩B)∩C⇔A∩(B∩C)
- 分配則
- A∪(B∩C)⇔(A∪B)∩(A∪C)、 A∩(B∪C)⇔(A∩B)∪(A∩C)
- 吸収則
- A∪(A∩B)⇔A、 A∩(A∪B)⇔A
- ド・モルガンの法則
- (A∪B)⇔A∩B、 (A∩B)⇔A∪B