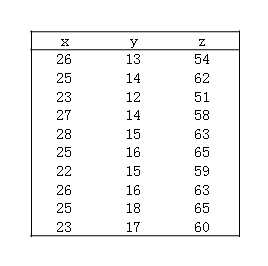
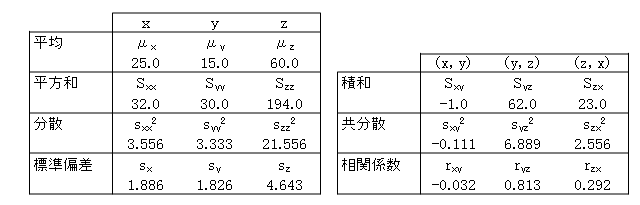
ここで用いる標本と、それによる統計量および記号を掲げます。
(別ウインドウで開く) (計算例)
計算方法の概略を示します。
自由度:標本数n=10なので、φ=n-1=9
平均:μx=Σxi=(26+25+・・・+23)/10=25
平方和:Sxx=Σ(xi-μx)2=(26-25)2+(25-25)2+・・・+(23-25)2=32.0
分散:sxx2=Sxx/φ=32.0/9=3.556
標準偏差:sx=√sxx2=√3.556=1.886
積和:Sxy=Σ(xi-μx)(yi-μy)=(26-25)(13-15)+(25-25)(14-15)+・・・+(23-25)(17-15)=-1.0
共分散:sxy2=Sxy/φ=-1.0/9=-0.111
相関係数:rxy=sxy/√(sxsy)=Sxy/√(SxxSyy)=-1.0/√(32.0×30.0)=-0.032
単相関と単回帰(復習)
単相関と単回帰について、簡単に復習しておきます。
ここでは、変数をxとzにします。
変数xとzの相関係数rzxは、
rzx=Szx/√(SxxSzz)=23.0/√(32.0×194.0)=0.292
となります。
また、xを説明変数、zを被説明変数とし、回帰直線を
z=a+bx
とすると、bを回帰係数といい、
bx→z=Szx/Sxx=23.0/32.0=0.72
となります。
(bx→z/rzx=√(Szz/Sxx)=sz/sx の関係、すなわち、回帰係数は相関係数を標準偏差で調整した関係があります)
定数項aは、この直線が点(μx, μz)を通ることから、
60.0=a+0.72×25.0 ∴ a=42.0
となるので、回帰直線は次式になります。
z=42.0+0.72x
この回帰直線により計算したzの値をz*としたとき、
εi=zi-zi*
を残差といいます。この残差εは、説明変数xの影響を取り除いたものであり、残差εとzの相関係数 rεz=0となります。このように、相関がない2変数の関係を「互いに直交する」といいます。
互いに直交する変数では、平方和の加法が成立するので、次の関係が成立します。
Σ(z-μz)2=Σ(z-z*)2 + Σ(z*-μz)2
(全変動) (回帰による変動)(残差による変動)
そして、寄与率あるいは決定係数を
回帰による変動 Σ(z-z*)2
r2=────────=───────
全変動 Σ(z-μz)2
と定義します。これは、回帰直線の当てはまりの度合いを示す尺度です。(計算例)
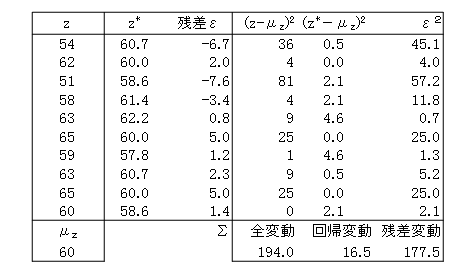
全変動=回帰変動+残差変動→194.0=16.5+177.5
r2=回帰変動/残差変動=16.5/177.5=0.0852
これは、r=0.282から計算したr2=0.2822=0.0852と一致
偏相関係数と偏回帰係数
変数が3つ以上の重回帰、重相関では、相関係数、回帰係数に相当する偏相関係数、偏回帰係数が重要な概念になります。かなり複雑になります。
偏相関係数
変数がx,y,zの3つがある場合、(x,y)、(y,z)、(z,x)について3つの相関係数が考えられます。
rxy=-0.032
ryz= 0.813
rzx= 0.292
rzx は、変量がxとzの2つだけのときの、xとzの関係を示す尺度ですが、ここではyが存在しているので、それによる影響を受けます。
例えば、xを身長、zを体重、yを胸囲とすれば、rzx は、胸囲を考慮せずに、身長と体重の関係を求めています。これは、胸囲は体重や身長には無関係だ(互いに直交している)という仮定をしているといえます。ところが実際には、胸囲が大きい人は体重が大きいだけでなく、身長も大きいという傾向があるでしょう。そうなると、rzx が身長と体重の「純粋な」関係を示しているとはいえません。
xとzの相関から、yの影響を取り除いたyとzの相関を偏相関、その度合いを偏相関係数といい rzx.yとします。
3つの変数間での相関関係を図示すると次のようになります。
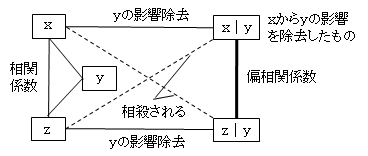
ここで、z|yは、zからvの影響を除いた残差ですから、zをyのみで単回帰したときの残差εy→zになり、x|yは、xをyのみで単回帰したときの残差εy→xになります。すなわち、rzx.yはこの残差同士の相関になります。
回帰式は、次のようになります。
y→z: z=29.0+2.066y
y→x: x=25.5-0.033y
当然、残差の平均は0です。平方和および積和は、次のようになります。
Σεy→z2=65.87
Σεy→x2=31.97
Σεy→zεy→x=25.07
これから、偏相関係数 rzx.y=25.0/√(65.87×31.97)=0.546
となります。
元の標本にまで戻らなくても、2変数の相関係数から偏相関係数を求めることができます(証明略)。
rzx.yは次の式により計算できます。
rzx-ryzrxy
rzx.y=─────────────=0.546
√(1-ryz2)√(1-rxy2)
同様に、xの影響を除いたyとzの偏相関係数は、
ryz-rxyrzx 0.813-0.032×0.292
ryz.x=─────────────=───────────────=0.860
√(1-rxy2)√(1-rzx2) √(1-(-0.032)2)×√(1-0.2922)
参考までに、zの影響を除いたuとyの偏相関係数は、
rxy-rzxryz
rxy.z=─────────────=-0.484
√(1-rzx2)√(1-ryz2)
となります。
偏回帰係数
偏回帰係数とは、他の説明変数を一定にして、その説明変数を1だけ増加させたときの被説明変数の平均的な増加量を意味します。
すなわち、回帰式、
z=a+bx+cy
のbがxのzに対する偏回帰係数 bx、cがxのzに対する偏回帰係数 by になります。
単にこれらの値を求めるだけならば、最小二乗法のほうが簡単です(→参照:「多項式、高次式での最小二乗法」)。実際に計算すると、次の回帰式が得られます。
z=9.00+0.784x+2.092y
b=bx c=by
しかし、最小二乗法では回帰分析による豊富な情報が得られません。それで、以下のような考え方が必要なのです。
最小二乗法では、次の連立方程式を解くことにより、a,b,cが求められます。
n・a + Σx ・b + Σy ・c = Σz
Σx・a + Σx2・b + Σxy・c = Σzx
Σy・a + Σxy・b + Σy2・c = Σzy
数値をあてはめると、
10a+ 250b+ 150c= 600
250a+6282b+3749c=15023
150a+3749b+2280c= 9062
これを解いて、
a=9.00
b=0.784・・・bx
c=2.092・・・by
が得られます。
z=9.00+0.784x+2.092y
xのzに対する偏回帰係数とは、yの影響を除去したときの、xがzに与える影響ですから、偏相関係数で行ったように、zをyのみで単回帰したときの残差εy→zと、xをyのみで単回帰したときの残差εy→xが対象になります。
すなわち、xのzに対する偏回帰係数とは、εy→zを被説明変数、εxyを説明変数としたときの、回帰係数だといえます。
偏回帰係数は次の式で与えられます。そして、この式の右辺の先頭項を標準偏回帰係数といいます。
rzx-ryzrxy sz 0.292-0.813×(-0.032) 4.643
bx=────────×──=───────────×───
1-rxy2 sx 1-(-0.032)2 1.886
=0.318×2.462=0.784
標準偏回帰係数 偏回帰係数
同様に、xを除いたときのyとzの偏回帰係数と標準偏回帰係数は、次のようになります。
となります。
ryz-rzxrxy sz 0.813-0.292×(-0.032) 4.643
by=────────×──=───────────×───
1-rxy2 sy 1-(-0.032)2 1.826
=0.823×2.523=2.092
標準偏回帰係数 偏回帰係数
aは、この直線が平均の点を通ることから、
μz=a+bxx+byy
より求められます。
すなわち、数値例では、
z=9.00+0.784x+2.092y
となります。
偏回帰係数の分子・分母を、それぞれ標準偏差で割っています。偏回帰係数は、説明変数の値の大小(単位の取り方など)により、変化してしまうので、それを除去するために、平均値=0,分散=1 に標準化(標準化)するのです。それが標準偏回帰係数です。標準偏回帰係数は、被説明変数への影響の大小を比較するのに用いられます。
先に「単回帰と単相関」で、回帰係数は相関係数を標準偏差で調整した関係にあるといいましたが、そうすると、標準偏回帰係数は相関係数に似た意味づけが連想されます。bxでの標準偏回帰係数と偏相関係数 rzx.y を比較してください。rzx.y の分母の ryz を rxz に変えただけです。
重相関係数
重回帰も単回帰のときと同様に、zと回帰式による計算値z*から、決定係数R2は
回帰変動 Σ(z-z*)2
R2=─────=───────
全変動 Σ(z-μz)2
あるいは、
残差変動 残差2 46.2
1-R2=────=───=───=0.127 ∴R2=0.873
全変動 Szz 194.0
と定義できます。そして、その平方根を重相関係数といいます。
なお、単相関係数にはrを用い、重相関係数にはRを用いることになっています。
Excelによる計算
上述のように、重回帰では複雑な式が用いられますが、実務には、Excelの「データ分析」に「分散分析」を用いることにより、容易に計算できます。
数値例を用いて、回帰式を z=a+bx+cy としたときのExcelによる結果出力例を掲げます。
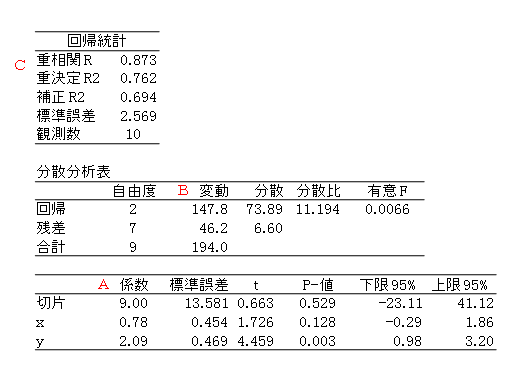
- 回帰式(A)
係数は偏回帰係数のことです。すなわち、回帰式は次式になります。
z=9.00+0.78x+2.09y - 変動(B)
回帰の変動は回帰変動、残差の変動は残差変動でε2、合計の変動は全変動でSzzのことです。 - 重相関係数(C)
重相関Rとは重相関係数Rのこと、重決定R2とはR2のことです。