秘書問題の定義
条件
- 必ず1人の秘書を採用する。
- 候補者数(すなわち最大面接回数)nは事前に決められている。
- 面接の直後に採否を決定する。
(n-1回まで採用しなかったときは、n番目の候補者を無条件で採用する) - 候補者側は、採用拒否をしない。採用が決まった時点で終了する。
(この条件により、「お見合い問題」や「結婚問題」というのは不適切?) - 過去に遡って不採用にした候補者を採用することはできない。
- 評価基準は決まっており、同順位の候補者は存在しない。
(候補者を同時に評価すれば、第1順位、第2順位~第n順位をつけることができる) - どの順番で、どの順位の候補者が現れるかはわからない。
ゲーム
「条件」のゲームをしましょう。20名の候補者がいます。各人の評価はあらかじめ乱数により与えられ、それにより絶対順位が付けられていますが、あなたはそれを知りません。あなたがわかるのは、それまでに採用しなかった候補者のうちでの暫定順位だけです。候補者が入室するたびに、選択ダイアログが表示され、採用(OK)/不採用(キャンセル)をクリックします。採用したときにゲームが終了し、その候補者の絶対順位が表示されます。
絶対順位が上位の候補者を採用できる戦略を考えてください。
最適化戦略
何をもって「最適」とするかにより、異なる2つの問題になります。
興味のある結果
理論は後回しにして、興味のある結果を掲げます。
候補者が20人(n=20)の場合
最良選択問題 順位最小化問題
面接回数 順位1の人を 採用する過去候
採用できる確率 補者での暫定順位
1 0.0500 見送り(不採用)
2 0.1774 :
3 0.2548 :
4 0.3072 :
5 0.3429 :
6 0.3661 1位なら採用
7 0.3793 :
8 0.3842(最大) :
9 0.3820 :
10 0.3735 :
11 0.3594 2位以内なら採用
12 0.3403 :
13 0.3167 :
14 0.2889 3位以内なら採用
15 0.2573 :
16 0.2221 4位以内なら採用
17 0.1836 5位以内なら採用
18 0.1420 7位以内なら採用
19 0.0974 10位以内なら採用
20 0.0500 無条件で採用
- 最良選択問題では、7回までは無条件で不採用にし(見送り)、8回以降は、それまでに不採用にした人との比較で(暫定順位が)1位ならば採用、そうでなければ不採用にして、次回の面接を行うのが最適である。
- この「8」回の値は、nの大きさに関係なく、n×37%で与えれれる。
正確にはn/e、e=2.718(自然対数の低) - そのときの確率は、nが大きくなると、1/eに近づく。
- 順位最小化問題では、次の3期にわけられる。
初期:ほぼn/4回まで。ともかく見送る。最良選択問題より短い
中期:ほぼn/2回まで。暫定順位が1位なら採用
後期:後半。次第にレベルを下げる。
(後半の順位が緩くなるのは、不採用者が増えるからでもある。) - この方法によれば、nが大きいときには、期待値は3.87に近づく。
すなわち、nによらず順位の期待値は4位以内となる。
任意のnでの計算には、末尾に「計算プログラム」があります。
最良選択問題
最良の(順位1)の候補者を採用できる確率の最大化
問題の理解
現在の面接をr番目の面接だとします。これまでにr-1人の候補者と面接して不採用にしました。r番目の面接者が、不採用にした候補者より評価が高ければ(順位が最小ならば)採用して面接を完了、そうでなければこの候補者も不採用にして、次の候補者と面接するという方法をとります。
このとき、最も評価の高い(順位1)の候補者をAとします。「Aを採用する確率を最大にするには、最初の見送る回数r-1をいくつにすればよいか」という問題です。
話を単純にするため、n=5とし、順位1の候補者をA、順位2をB、~、順位5をEとします。
- r=1:最初の面接にきた候補者を採用する。
Aが最初にくる確率は、P(1)=1/n=1/5=0.2です。 - r=5:最後まで待つ。
Aが最後にくる確率も、P(5)=1/n=1/5=0.2になります。
(すでに不採用にした4人のなかにAもいると考えるのが常識的でしょう) - r=2:1人Xが不採用になっています。現在の面接者がXより良ければ採用します。
- X=Aの場合
面接者を含む残りの4人にはAはいません。すべて不成功。確率=0 - X=Bの場合
残りの4人のうち、A以外ならばBよりも劣るので不採用を続けていけば、いつかはAがくるので、かならず成功します。確率=1 - X=Cの場合
残りの4人のうち、採用されるのは、AかBのどちらかです。Aが先にくれば成功、Bが先にくれば不成功です。確率=1/2 - X=Dの場合
A~Cの3人のうち、Aが最初にくれば成功。確率=1/3 - X=Eの場合
A~Dの4人のうち、Aが最初にくれば成功。確率=1/4
P(2)=(1/5)×(0 + 1 + 1/2 + 1/3 + 1/4)=0.4167
となります。これは、P(1)、P(5)より大です。 - X=Aの場合
すなわち、面接回数rと、面接したr人での最良の順位sだけから、成功確率P(r) を計算して、P(r) が最大となるrを求める問題だと理解できます。
定式化
n人の候補者からr人の候補者と面接したとき、順位1の候補者が得られる確率P(r) を求める手順を考えます。
先に不採用にしたr-1人のうち、最良の順位をsとします。
そのr-1人のなかにAがいない確率は(r-1)/nです。
現在面接している人を含めて、残っている候補者のうち、sよりも順位がよい候補者はn-s人ですから、現在面接している人がAである確率は1/(n-s)です。
すなわち、r-1人のうち最良の順位がsで、r番目の面接者がAである確率p(r,s)は、
p(r,s)=(r-1)/n×1/(n-s)
となります。
sの範囲はr-1≦s≦nですから、
P(r)=p(r,r-1) + p(r,r) + p(r,r+1) + ・・・ + p(r,n)
となります。
これから、次の公式が得られます。
n人の候補者からr人の候補者と面接したとき、順位1の候補者が得られる確率P(r) は、
P(r)= (r-1)/n ×{1/(r-1) + 1/(r) + ・・・ + 1/(n-1)} ・・・公式1
P(1)= 1/n
n=5、10、20 のときの P(r) の表を掲げます。(*)は最大値
r n=5 n=10 n=20
1 0.2000 0.1000 0.0500
2 0.4167 0.2829 0.1774
3 0.4333(*) 0.3658 0.2548
4 0.3500 0.3987(*) 0.3072
5 0.2000 0.3983 0.3429
6 0.3728 0.3661
7 0.3274 0.3793
8 0.2653 0.3842(*)
9 0.1889 0.3820
10 0.1000 0.3735
11 0.3594
12 0.3403
13 0.3167
14 0.2889
15 0.2573
16 0.2221
17 0.1836
18 0.1420
19 0.0974
20 0.0500
最大化
公式1は、次のように変形できます。
P(r)= 1/n×{1 + (r-1)/(r) + ・・・ + (r-1)/(n-1)}
r→r+1 では、
P(r+1)= 1/n×{ r/(r) + ・・・ + r/(n-1)}
従って、
P(r+1)-P(r)=1/n×{-1 + 1/r + 1/(r+1) + ・・・ + 1/(n-1)}
となります。
最大にするrとは、P(r+1)<P(r) となる直前のrですから、
1/r + 1/(r+1) + ・・・ + 1/(n-1) <1
となるrを求めることになります。
ここで、nが十分大きいときには、
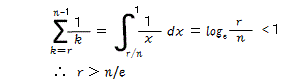
となります(e は自然対数の低で、e=2.718、1/e=0.3679 です)。
n人の候補者から順位1の候補者が得られる確率P(r) を最大にするrは、
r= n/e (小数点以下切り上げ) ・・・公式2
e=2.718(自然対数の低)
である。
すなわち、最初のr-1=n/e≒0.37(小数点以下切り捨て)回は、見送って不採用にし、r回以降は、不採用にしたr-1人よりもよい候補者がきたら採用するという戦略をとるのが最適だということになります(37%の法則)。
n=5、10、20 のときを計算すると、それぞれr=2、4、8となります。n=5のときは「nが十分に大き」くないのでずれがありますが、n=10、20のときは、上の数表と一致しています。
なお、P(r) の最大値は、nが大きくなるにつれ減少し、n→∞で 1/e に収斂します。
順位最小化問題
最良選択問題では、順位1の候補者だけを対象にしましたが、順位最小化問題では、第1順位を1、第2順位を2・・・としたとき、採用する候補者の順位の期待値を最小にすることを目的にします。「最良の人でなくても、なるべく優れた人を採用したい」という目的です。
当初は、最良選択問題と同様に見送るでしょう。中段では、まだ順位1の候補者を求めることができましょう。s=1なら採用するというのが最適でしょう。ところが、後段になると、優れた人を不採用しているので、不採用の人よりも劣っていても仕方がないことになります。
すでにr-1人の候補者を不採用にしており、r番目の候補者Aと面接している。不採用者と比較したAの暫定的な順位をsとするとき、sがどれだけ以下ならば採用(sより大ならば不採用として次の面接を行う)のが最適な戦略になるかという問題になります。
問題の定式化
n人の候補者のうち、r(≦n-1)人を不採用にしているとき、最終的に採用する人の順位の期待値をα(r) とします。
r=n-1のときは、最後の候補者を無条件で採用します。その期待値は1~nの平均値ですから、
α(n-1)=(n+1)/2
になります。
r<n-1について考えます。r番目の候補者をAとします。
Aおよびこれまで不採用にしてきた候補者のなかでのAの暫定順位をsとして、例えばs≦5ならば採用、s>5ならば不採用として、次回の面接に期待するという戦略をたてることにします。
このときの最良の戦略は、
Aを採用したときの順位の期待値+Aを採用しないときの順位の期待値
を最小にするsを決めることです、
sを厳しくしてそれにかなう候補者が現れれば、期待値は小さくなりますが、そのような候補者が出現する確率は低いでしょう。
候補者全員nのなかでのAの真の順位の平均は (n+1)/2 で、Aを含めたrのなかでのAの暫定順位の平均は (r+1)/2 ですから、Aを採用したときの真の順位の期待値は、 s*(n+1)/(r+1) となります。
それで、s以内であれば採用するならば、Aを採用したときの期待値は
(1*(n+1)/(r+1) + 2*(n+1)/(r+1) + ・・・ + s*(n+1)/(r+1))/r
=(s/r)*(n+1)/(r+1)*(s+1)/2
s以内でなければ採用しないとすれば、Aを採用しない確率は (r-s)/r で、そのときは次回の面接での期待値が得られるのですから、この時点での期待値は (r-s)/r*α(r) です。
これから次の公式が得られます。
n人の候補者があり、r回目の候補者Aの暫定順位がs以内ならば採用するとしたとき、最終的に採用した候補者の順位の期待値E(r,s)は、次の漸化式で与えられる。
E(r.s)=(s/r)*(s+1)/(r+1)*(n+1)/2 + (r-s)/r*α(r), α(n-1)=(n+1)/2
そして、E(r.s)を最小とするs*(r) が、Aの採否の最適基準であり、s=*(r) での
α(r-1)=(s/r)*(s+1)/(r+1)*(n+1)/2 + (r-s)/r*α(r)
が最適決定を続けたときの候補者の順位の期待値となる。 ・・・公式3
このように、r=n→1 の逆順に、最適設定を繰り返すことにより、全体の最適化を図る技法を「動的計画法」といいます。
探索範囲の効率化
- α(n-1) = (n+1)/2 なのですから、r=n-1(最終面接)のときのAの最適暫定順位s*(r) は
s*(n-1) ≦ (n+1)/2
になるはずです。 - 例えば、18回目で順位が5位以内を採用としたとき、17回目で6位の候補者を選ぶのは不適切です。
s*(r-1) ≦ s*(r-1)
になります。 - また、18回目でのs*が5だとしたとき、17回目でのs*が急に2になるというのは不自然です。sの大きいほうから計算するのが得策です。
- E(r,s) は、sに関して単調増加、あるいは一つの谷がある曲線になります。sを大きいほうから計算していき、増加に転じる直前のsがs*(r) になります。
- rが小さくなるにつれて、s*(r) が小さくなり、α(r-1) の値も小さくなります。r=n/2付近になると1になります。さらに小さくなる(r=n/4付近)と、α(r-1) > α(r) になります。
これは、s=1ですら採用しないほうがよいことを示しています。すなわち「初期の面接では無条件で不採用にする(見送りをする)のがよい」ことを示しています。
α(r-1) > α(r)になったら、それ以降のrについて計算する必要はありません。
数値例
n=20とします。
α(n-1)=α(19)=(n+1)/2=10.5
r=19のとき
s s/r*(s+1)/(r+1)*(n+1)/2 (r-s)/r*α(r) E(r,s)
11 3.647 4.421 8.068
10 最適 3.039 4.974 8.013 最小→α(18)
9 2.489 5.526 8.013
8 1.989 6.079 8.068
7 1.547 6.632 8.179
すなわち、19回目の面接では、Aの暫定順位が10位以内ならば採用するのが最適であり(s
s=11は不要なのですが、参考として計算しました。Eは大きくなっており、そこまで緩やかにするのは不利なことを示しています。
r=18のとき
α(18)=8.013 なので、s≦8 を探せばよいことになります。
s E(r,s)
8 6.662
7 6.616 最小 α(17)
6 6.632
18回の面接では、Aの暫定順位が7位以内なら採用し(s*(19)=10)、そのときの順位期待値は 6.616(α(17)= 6.616)になります。
以下同様にして
r s*(r) α(r-1)
17 5 5.700
16 4 5.047
15 3 4.562
14 3 4.185
13 2 3.887
12 2 3.643
11 2 3.458
10 1 3.303
9 1 3.169
8 1 3.065
7 1 3.002
6 1 3.0017
r=5のとき
α(5)=E(5,1)=3.101 > 3.0017=α(6)
になってしまいました。最も厳しい条件、s=1 としても、採用せずに次回面接を待ったほうがよいという結果です。
r=4以降が、すべてこの結果になるのは明白で、ここで計算が終了します。
この数値例は、前述のの「興味のある結果」と一致しています。
αの最小値は、α(6)=3.0017 でした。見送り期間が終わったら、s=1の候補者が出現したら、直ちに採用に踏み切るのが最適であり、平均すれば20人中3位の人が得られることを示しています。
それよりも10回目でのs=1の候補者は、さらに優れているのだから、そこまで採用を伸ばすべきだと思うかもしれません。しかし、その頃になると、s=1になる確率が小さくなってしまい、全体の期待値が悪くなってしまうのです。
なお、この 3.0017 の数値は、nが大きくなるのにつれて大きくなりますが、n→∞でも 3.870 になることが証明されています(数学的に高度になるので割愛。私も理解不能)。すなわち、候補者数に無関係に、上位4位の候補者を選ぶことができるというのです。