動的計画法(Dynamic Programming)とは、最適性の原理を用いて、多段決定問題を取り扱うOR技法です。
最適性の原理とは、「決定の全系列にわたって最適化を行うためには,初期の状態と最初の決定がどんなものであっても,残りの決定は最初の決定から生じた状態に関して最適な政策を構成していなければならない」(JISの定義)ということです。いいかえれば、「全体が最適化されたときは、その部分も最適化されている」ということです。
最短経路問題による考え方の説明
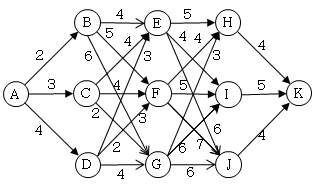
例えば、次のような経路と所要時間があるとき、AからKまで行く時間を最小になる経路を探すとき、全体の最短経路がGを経由するとすれば、AからGまでの最短経路がわからなくても、GからKまでは最短経路になっていなければならないということです。
→詳細説明と計算プログラム:「最短経路問題」(or-dp-shortpath)
最適配分問題による最適性の原理の説明
動的計画法では、小さな部分問題を計算して得られた解を記録しておき、それを、さらに大きい問題を解くために有効に使うことが特徴です。
例えば、いくつかの投資案について、投資資金と利益の表が与えられ、全体の投資上限額が与えられたとき、利益を最大にするために、どのように資金を配分すべきかという問題を考えます。
投資iにxi万円を配分したときの利益を、fi(xi) 万円とし、全体の投資上限額をQmax万円とすれば、
目的関数:f1(x1) +f2(x2) +・・・+fn(xn) →最大
制約条件: x1+x2+・・・+xn=Q≦Qmax
と定式化されます。
まず、投資案1に、x=0,1,2,・・・,Qmax万円かけたときの最大利益 P1(x) は f1(x) になります。P1(x) を記録しておきます。
次に投資案2を加えてx万円を配分すると、投資案2から f2(x) の利益があり、それまでの投資への配分は Q-x万円になるので、その利益は P1(Q-x) となります。それで、投資案2を加えたときの最大利益 P2(x) は、
P2(x) =max{f2(x) + P1(Q-x)} x=0,1,2,・・・,Q
となります。
これを一般化すれば、
Pi(x) =max{fi(x) + Pi-1(Q-x)} x=0,1,2,・・・,Q
になります。このようにして、投資nまでを行えば、全体の最適配分を求めることができます。
ここで、fi(x) + Pi-1(Q-x) を最大とするxの値を xi(Q) に記録しておくと、次に加えられる投資のいかんにかかわらず、投資iまでの配分がkだとすれば、その配分構成 xi(Q) は変わらないことになります。これが最適性の原理です。
→詳細説明と計算プログラム:「動的計画法による最適配分問題」(or-dp-max)
ナップザック問題による計算量の説明
最適配分問題を拡張したものにナップザック問題があります。
ナップザック問題とは、ナップザックには最大重量が Qmax であり、入れたい品物の重量 wi と、入れることによる利益 wi が与えられているとき、利益を最大にするには、どの品物を選択すればよいかという問題です。次の式で表現できます。
目的関数:f1xi + f2xi + ・・・ + fnxi →最大
制約条件:w1xi + w2xi + ・・・ + wnxi =Q≦Qmax
これは、最適配分問題と同じような手順で解くことができます。
→詳細説明と計算プログラム:「ナップサック問題」(or-dp-knapsack)
とくに、同一の品物が1個だけのとき(xi が0または1だけのとき)を0-1ナップザック問題といいます。それを例にして、動的計画法により計算量が小さくなる(短時間で計算できる)ことを示します。
品物の個数がnであるとき、すべてのケースを総当たりで調べる方法では、品物iを選択するかどうかの2通りなので、n個では 2n 回になり、最大利益を探すのにn回の計算が必要になるので、全体として 2×nn 回の計算が必要になります。そのため、nが大きくなると、実際に解くことが不可能です(そのような問題をNP完全問題といいます)。
それに対して動的計画法を用いると、「品物iを加えたときに、n回の計算をして最大利益を得る」計算をiを1からnまで行うのですから、n2 に比例した回数でよいことになります。