割当問題

割当問題の概要

割当問題とは、ｎ人の作業員とｎ個の作業があり、作業員ｉが作業ｊに従事したときの費用 ｃ[ｉ][ｊ] が与えられているとします。そのとき、総費用を最小にするには、誰をどの作業につければよいかという問題です（ｃ[ｉ][ｊ] が効果で、総効果を最大にするのであれば、ｃの値に－１をかければよい）。

作業員ｉが作業ｊに従事する値を ｘ(ｉ,ｊ)（０または１の値）として、線形計画法で定式化すると、次のようになります。
　　目的関数
　　　Ｚ＝c(1,1)x(1,1) + c(1,2)x(1,2) + ・・・ + c(1,n)x(1,n)
　　　　+ c(2,1)x(2,1) + c(2,2)x(2,2) + ・・・ + c(2,n)x(2,n)
　　　　　　・・・・・・
　　　　+ c(2,1)x(2,1) + c(2,2)x(2,2) + ・・・ + c(2,n)x(2,n) →最小
　　従業員による制約式
　　　　　x(1,1) + x(1,2) + ・・・ + x(1,n) ＝１
　　　　　x(2,1) + x(2,2) + ・・・ + x(2,n) ＝１
　　　　　　・・・・・・
　　　　　x(n,1) + x(n,2) + ・・・ + x(n,n) ＝１
　　従業による制約式
　　　　　x(1,1) + x(2,1) + ・・・ + x(n,1) ＝１
　　　　　x(1,2) + x(2,2) + ・・・ + x(n,2) ＝１
　　　　　　・・・・・・
　　　　　x(1,n) + x(2,n) + ・・・ + x(n,n) ＝１

これを線形計画法の整数計画法として解くこともできますが、式の特徴に注目すると、もっと簡単に解くことができます。その手順は、次の通りです。

ステップ１：正規化

最大値問題の場合は、行列の表を－１倍して最小化問題にする。
各行につき、その行での最小値を減じる。
各列につき、その列での最小値を減じる。

ステップ２：最適性の評価

すべての０要素をカバーする最小限の線を引く。
その数が表のサイズであれば、最適解である。

ステップ３：解の改善

線が引かれていない要素の最小値を求める。
線の引かれていない要素から最小値を減じる。
交点になっている要素に、最小値を加える。

割当問題の数値例

問題

５人の作業員と５個の作業があり、その費用が下表のように与えられている。例えば、作業員１を作業３に割り当てると４の費用がかかり、作業員２を作業３に割り当てると２の費用がかかる。総費用を最小にするには、どのように割りつければよいか。
　　　　　　　　　　　作　業
　　　　　　　　１　２　３　４　５
　　　　　　　┌─────────┐
　　　　　　１│９　５　１　９　７│
　　　　作　２│２　８　２　７　５│
　　　　業　３│１　３　９　５　９│　　　　表１
　　　　員　４│８　７　２　６　４│
　　　　　　５│２　３　６　２　８│
　　　　　　　└─────────┘

正規化

ここで、「作業員１をどの作業に割り当てても、ａ円の費用が余計にかかる」として、行１の各要素にａを加えても（減じても）問題の本質は変わりません。それで、各行からその行のなかでの最小値を減じた表を作成します。
　　　　　　　１　２　３　４　５
　　　　　　┌─────────┐最小値
　　　　　１│８　４　０　８　６│　１
　　　　　２│０　６　０　５　３│　２
　　　　　３│０　２　８　４　８│　１　　　表２
　　　　　４│６　５　０　４　２│　２
　　　　　５│０　１　４　０　６│　２
　　　　　　└─────────┘

同様に、ある列から、その列の各要素に同じ数値を加減しても、問題の本質は変わりません。それで、各列からその列のなかでの最小値を減じた表を作成します。
　　　　　　　１　２　３　４　５
　　　　　　┌─────────┐
　　　　　１│８　３　０　８　４│
　　　　　２│０　５　０　５　１│
　　　　　３│０　１　８　４　６│　　　　　表３
　　　　　４│６　４　０　４　０│
　　　　　５│０　０　４　０　４│
　　　　　　└─────────┘
　　　最小値　０　１　０　０　２

このような操作をすることを正規化といいます。表１でも正規化した後での表３でも、最適解は同じになります。それで、以降は表３が与えられたこととします。

最適性の評価

表３において、０となっている要素は、このように割り当てると費用が０になることを示しています。それで、例えば表４のように「各行・各列に０があるように選ぶことができれば、その０の要素が最適な割り当てを示す最適解である」（◎は選ばれた０の要素）といえます。ところが、表３ではうまく割り当てることができません。

ここで、次の問題が発生します。
・どうすれば◎を付けることができるかどうかを確認できるのでしょうか？
・表３の場合には、さらに手を加えて表４のように変形する必要がありますが、
　どのような操作をすればよいでしょうか？

理由は省略して、手順だけを示します。

1. 線の本数が最小で、すべての０の要素をカバーするように線を引く。
2. その線の数が、行（列）の数（ここでは５）必要であれば最適解である。
   その理由は、◎となる要素を（ｉ,ｊ）とすれば、必ず行ｉかｊの一方に線を引く必要があり、以前に線を引いたところは、既にその行か列に◎があるから、重複して◎にすることができないこと、そして、線が５本になったことは、◎が５つあることから説明できます。
3. 線の数が行数よりも少なければ、最適解ではなく、改善をする必要がある。

解の改善

改善の方法は、次の手段で行います。

1. 線が引かれていない全要素の最小値を探す。
2. 線が引かれていない要素については、最小値を減ずる。
3. 交点になっている要素については、最小値を加える。

表３について、この手順を行うと次のようになります。

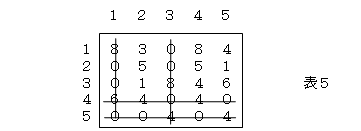
• ４本の線ですべての０要素をカバーできました。→改善の必要あり。
• 線が引かれていない要素での最小値＝１
• 線の引かれていない要素から最小値を減じ、交点の要素には最小値を加える。

この結果は、表６（すなわち表４）になります。

この例では、１回の改善で最適解になりましたが、最適解を得るまで「最適性の評価」と「解の改善」を繰り返し行います。

ここで、最小値を減じたり加えたりすることは、「正規化」で行や列から同じ値を加減することと同じです。「解の改善」の内容は、
　線に関係なく、すべての要素から最小値を減じる。
　線の引かれた行の要素に最小値を加える。列についても同様である。
ことと同じです。それで、それで、
　　　なぜ、線を引いた行や列を特殊視するのか？
がポイントになります。
　その理由は（厳密ではありませんが）、表５のような線の引き方では可能解が得られないので、まだ線が引かれていない要素のなかで、新規に０となる要素を探したいからです。
　それには、表３が最適解になっていれば総費用が０になって理想的なのですが、それでは不可能ですので、少し条件を緩めて、「最小値」位は費用がかかってもよいと仕方がないとするのです。また、「最適性の評価」と「解の改善」を繰り返し行うのは、可能解が得られるまで、条件を緩めているのだと解釈できます。
　可能解になったときが最適解であることは、そのつど「最小値」を用いていることから理解できます。

なお、厳密な説明をするので、双対問題の適用が必要になりますが、ここでは省略します。

練習問題

　　　　　　　１　２　３　４　５
　　　　　　┌─────────┐
　　　　　１│１　３　４　５　２│
　　　　　２│３　５　２　２　６│
　　　　　３│１　２　５　８　５│
　　　　　４│２　３　４　６　２│
　　　　　５│２　５　１　３　４│
　　　　　　└─────────┘
（解答）

計算プログラムについて

ここで掲げた解法で
　　・線の本数が最小で、すべての０の要素をカバーするように線を引く。
ことは、表を目視して線を引くのは比較的簡単なのですが、そのアルゴリズムをプログラミングすると、私の能力では、しかるべき計算量で達成することができず、現在放棄したままになっております。
　ご指導いただければ幸甚です。