ご利用にあたって
線形計画法や動的計画法などの分野での基礎的な計算手法を JavaScript のライブラリとしてまとめたものです。
別シリーズ「Webテキスト」での活用を目的としたもので、小規模の素直な問題に限定されています。
単に結果を戻す「Return]タイプと、結果までの処理経過を示す「Trace」タイプがあります。
ソースコードを公開しています。ご利用は自由ですが、信頼性や効率性への保証はありません。
| mpLP | 線形計画法 | シンプレックス法による最適解と感度分析。基準形 |
| mpLP1 | 線形計画法 | シンプレックス法による最適解と感度分析。罰金法 |
| mpLP2 | 線形計画法 | シンプレックス法による最適解と感度分析。2段階法 |
| mpLPDual | 線形計画法 | 主問題→双対問題 |
| mpTrans | 輸送問題 | 北西隅の方法により初期解を得て、U-V法により解の改善を行い、最適解を求める |
| mpAssg | 割当問題 | ハンガリー法と全組合せスキャン法を示します。 |
| mpSaitekiHaibun | 最適資金配分問題 | 動的計画法により、制約条件:Q=x0 + x1 + x2 + ・・・ + xn ≦ Qmax 0 ≦ xi ≦ xmaxi の下で 目的関数:Rx = f(x0) + f(x1) + f2(x2) + ・・・ + fn(xn) を最大化する xi を求める。 |
| mpKnapsack | ナップザック問題/td> | 個数制約:0 ≦ x[i] ≦ 上限個数[i] 容量制約:∑w[i]*x[i] ≦ ナップザック容量 の制約で 目的関数:∑f[i]*x[i] を最大化する x[i] を求める問題。動的計画法 |

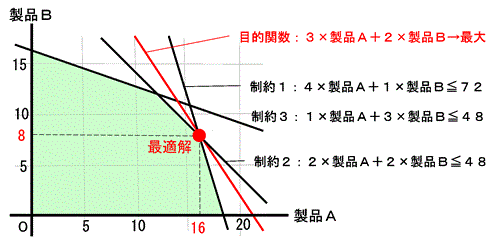
次の制約条件
制約1: 4*製品A + 1*製品B ≦ 72
制約2: 2*製品A + 2*製品B ≦ 48
制約3: 1*製品A + 3*製品B ≦ 48
の下で、目的関数
3*製品A + 2*製品B → max
のモデルを次のように記述します。
●比較子に "=" がある場合、感度分析表は不完全です。Infinity と表示されても、有限値であることがあります。
次の制約条件
制約1: 4*製品A + 1*製品B ≦ 72
制約2: 2*製品A + 2*製品B ≦ 48
制約3: 1*製品A + 3*製品B ≦ 48
の下で、目的関数
3*製品A + 2*製品B → max
のモデルを次のように記述します。
次の制約条件
制約1: 4*製品A + 1*製品B ≦ 72
制約2: 2*製品A + 2*製品B = 48
制約3: 1*製品A + 3*製品B ≧ 24
の下で、目的関数
3*製品A + 2*製品B → max
のモデルは次のようになります。
var 基幹変数名 = ["製品A","製品B"];
var 制約式名 = ["制約1","制約2","制約3"];
var 係数表 = [[4,1],[2,2],[1,3]];
var 比較子 = ["<","=", ">"];
var 定数項 = [72,48,24];
var 目的関数 = [3,2];
var MinMax = "max";
●比較子に "=" がある場合、感度分析表は不完全です。Infinity と表示されても、有限値であることがあります。
次の制約条件
制約1: 4*製品A + 1*製品B ≦ 72
制約2: 2*製品A + 2*製品B ≦ 48
制約3: 1*製品A + 3*製品B ≦ 48
の下で、目的関数
3*製品A + 2*製品B → max
のモデルを次のように記述します。
次の制約条件
制約1: 4*製品A + 1*製品B ≦ 72
制約2: 2*製品A + 2*製品B = 48
制約3: 1*製品A + 3*製品B ≧ 24
の下で、目的関数
3*製品A + 2*製品B → max
のモデルは次のようになります。
var 基幹変数名 = ["製品A","製品B"];
var 制約式名 = ["制約1","制約2","制約3"];
var 係数表 = [[4,1],[2,2],[1,3]];
var 比較子 = ["<","=", ">"];
var 定数項 = [72,48,24];
var 目的関数 = [3,2];
var MinMax = "max";
主問題:次の制約条件
制約1: 4*製品A + 1*製品B ≦ 72
制約2: 2*製品A + 2*製品B ≦ 48
制約3: 1*製品A + 3*製品B ≦ 48
の下で、目的関数
3*製品A + 2*製品B → max
のモデルを次のように記述します。
双対問題は、次のようになります。
変数1: 4*制約1 + 2*制約2 + 1*制約3 ≧ 3
変数2: 1*制約1 + 2*制約2 + 3*制約3 ≧ 2
の下で、
目的関数:72*制約1 + 48*制約2 + 48*制約3 → min
これをmax にするために、正負反転して
目的関数:-72*制約1 - 48*制約2 -8*制約3 → max
双対モデル(実行結果は別ウインドウに表示)
var 基幹変数名 = ["制約1", "制約2", "制約3"]; // ← 主制約式名
var 制約式名 = ["製品A","製品B"]; // ← 主基幹変数名
var 係数表 = [[4,2,1], [1,2,3]]; // ← 主係数表の転置行列
var 定数項 = [3, 2];< // ← 主目的関数
var 目的関数 = [-72, -48, -48]; // ← 主定数項
var 比較子 = [">",">"];
var MinMax = "max";
供給地iの供給量と需要地jの需要量と、i→jの単位輸送費用を与えて、総輸送費用を最小化するように、i→jの最適輸送量を計算します。
北西隅の方法により初期解を得て、U-V法により解の改善を行い、最適解を求めます。
すべての入力値は正の整数で、Σ供給量 = Σ需要量 でなければなりません。
問題
j 0 1 2 3
┌───────────────────┐
│需要地A 需要地B 需要地C 需要地D│ 需要地名
├───────────────────┤
i 供給地名 供給量 │ 12 20 16 18 │ 需要量
┌────┬───┼───────────────────┤
0 │供給地X│ 18 │ 7 3 2 10 │
1 │供給地Y│ 22 │ 9 3 6 8 │ 費用表(単価)
2 │供給地Z│ 26 │ 8 7 8 6 │
└────┴───┴───────────────────┘
入力データ
var 供給地名 = ["供給地X", "供給地Y", "供給地Z"];
var 供給量 = [18, 22, 26];
var 需要地名 = ["需要地A", "需要地B", "需要地C", "需要地D"];
var 需要量 = [12, 20, 16, 18];
var 費用表 = [ [ 7, 3, 2,10],
[ 9, 3, 6, 8],
[ 8, 7, 8, 6] ];
var rtn = mpTrans(費用表, 供給地名, 供給量, 需要地名, 需要量);
出力データ
rtn["輸送表"]
0 1 2 3
┌─────────┐
0 │ 2 0 16 0 │
1 │ 2 20 0 0 │
2 │ 8 0 0 18 │
└─────────┘
rtn["総費用"] = 296
0 1 2 3
┌──────────┐
│ 7 1 2 5 │ rtn["v"] 需要量を1増加したたときの総費用の増加
┌──┼──────────┤
0 │ 0 │ 0 2 0 5 │
1 │ 2 │ 0 0 2 1 │ rtn["評価表"] 輸送量を1増加したたときの総費用の増加
2 │ 1 │ 0 5 5 0 │
└──┴──────────┘
└ rtn["u"] 供給量を1増加したたときの総費用の増加
職務
0 1 2 3 4
┌─────────┐
0 │ 9 5 1 9 7 │
担 1 │ 2 8 2 7 5 │
当 2 │ 1 3 9 5 9 │
者 3 │ 8 7 2 6 4 │
4 │ 2 3 6 2 8 │
└─────────┘
割当問題とは、n人の担当者とn個の職務があり、それぞれの割当てによる金額表(効果あるいは費用の表)が与えられたとき、総金額が最大あるいは最小の割当を求める手法です。
ここでは、最小化を標準にしています。
最大化をするには、上の表の要素をすべて負数にすればよいのですが、正数にするため、表中の最大要素(金額表[0」[0]~=9)を見つけ、その値をzとして、全要素からzから引くのが一般的です。
しかしここでは MinMax を "max" とすることで、関数がこの操作を行います。
上例の最小化問題での割付表は、[ [0,2], [1,0], [2,1], [3,4], [4,3] ] になり、
金額は、1 + 2 + 3 + 4 + 2 = 12 になります。
私の能力により、次の限界があります。
ハンガリー法の特徴は「0要素を網羅する最小個数の線を引く」ことにあります。目視で試行錯誤するのは比較的容易ですが、私にはそのアルゴリズムを作れませんでした。それで「0の個数が最大になる行、あるいは列に線を引く」ことの繰り返せば少ない線数になるだろう」という手段にしていますが、それが最小であるとの保証はありません。不完全な段階で最適と判断する危険性があります。
最適解に到達したとき、「行あるいは列で0の個数が一つのものが最適割当だ」としています。そのため複数の解があるときの判断ができず、最適割当が存在しないとい結論になる危険性があります。
入力
var MinMax = "min";
var 金額表 = [ [3, 8, 1, 2],
[3, 2, 4, 5],
[3, 1, 2, 4],
[7, 4, 2, 2] ];
var 割当表 = mpAssgHun(MinMax, 金額表);
出力
割当表 = [[0,2],[2,1],[1,0],[3,3] ];
(担当者0は職務2、担当者2は職務1、… に割当)
担当者、職務の数がnのとき、n!通りの組合せがあります。それぞれに金額表の値をtれて計算すれば、最小化・最大化での最適割当が求められます。複数解のすべてを発見できます。
最も確かな解法ですが、nが大きくなると極度に計算負荷が増大します。n<8程度が限度でしょう。
入力
var MinMax = "min"; // 最小化
職務
0 1 2 3 4
var 金額表 = [[1, 3, 4, 5, 2], // 0
[3, 5, 2, 2, 6], // 1 担
[1, 2, 5, 8, 5], // 2 当
[2, 3, 4, 6, 2], // 3 者
[2, 5, 1, 3, 4]]; // 4
var 割当表 = mpAssgScan(MinMax, 金額表);
出力
割当表 = [[0,2,4,1,3]]
職務0 には 担当者0 、職務1には 担当者2、職務2には 担当者4 … が最適割当になる。
最適解が複数になることもあり。割当表は2次元配列になる。
動的計画法により、
制約条件:Q=x0 + x1 + x2 + ・・・ + xn ≦ Qmax 0 ≦ xi ≦ xmaxi
の下で
目的関数:Rx = f(x0) + f(x1) + f2(x2) + ・・・ + fn(xn) →最大
を最大化する xi を求めます。
これは、「n個の投資案件があり、案件iに xi の資金を配分したときの利益が fi(xi) であるとしたとする。全投資のための資金の上限がQmaxであるとき、利益最大にする各投資への資金配分額を求めよ。」という意味です。
ここでは、単純にするために、f(xi) を 数値 f[x][i] で指定し、前の f[x][i-1] との間を
step [i] までは f[x][i-1]で [i]になったら階段状に f[x][i] になる。
line 2点を直線で結ぶ
で指定します。これは f[x] 全体に適用されます。
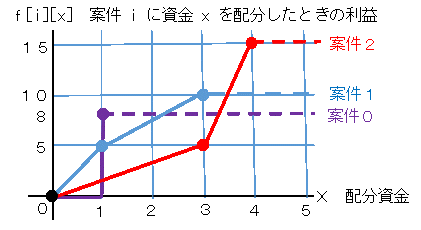
案件0,1,2の案件への資金配分による利益が右図のとおりだとします。
点線の部分は、これ以上配分しても利益は変わらない(無駄な配分)ことを示します。
それを、下の利益表の形式で記述します。
解は、最適解のように2次元表で得られます。
解は与えた全資金だけでなく、資金が0,1.2,…、全資金について得られます。
入力
var 全資金 = 8;
// type x0,f0 x1,f1
var 利益表 = [ ["step", 1, 8 ], // 案件0
["line", 1, 5, 3,10 ], // 案件1
["line", 3, 5, 4,15 ] ]; // 案件2
var 最適解 = mpSaitekiHaibun(全資金, 利益表):
出力(最適解)
案件0 案件1 案件2
資金 利益 資金 利益 資金 利益
q↓i→ 0 1 2 3 4 5
0 0 0 0 0 0 0
1 1 8 0 0 0 0
2 1 8 1 5 0 0
3 1 8 2 7.5 0 0
4 1 8 3 10 0 0
5 1 8 0 0 4 15
6 1 8 1 5 4 15
7 1 8 2 7.5 4 15
8 1 8 3 10 4 15
ナップザック問題とは、n個の品物について、体積 w[i] とナップザックに入れることの利益 f[i] を与えて、
個数制約:0 ≦ x[i] ≦ 上限個数[i]
容量制約:∑w[i]*x[i] ≦ ナップザック容量
の制約で
目的関数:∑f[i]*x[i]
を最大化する x[i] を求める問題です。
その代表的解法として最適性の原理による動的計画法があります。
何らかの方法で i-1 までの品物について、容量 q を配分したときの最適配分 p[i-1][q] が求められているとします。
i = 0 のとき、一つしか品物がないので p[0][q] = f[0]*x[0] です。
品物 i を追加したとき、
a:品物 i を入れなかったとき、その利益は p[i-1][q] のままです。
b:x[i] 個入れるときの利益は、次の合計になります。
品物 i での利益は、f[i]*x[i] となり、w[i]*x[i] の容量を使います。
品物 i-1 までの利益は、容量残 = q-w[i]*x[i] なので p[i-1][容量残] になります。
aが大ならば、品物iを入れないので、以前の品物構成は変わらない
bが大ならば、品物iを入れる。以前の最適配分は p[i-1][容量残]
これにより、品物 i を追加したときの最適配分 p[i][q] が求められます。
このようにして、全部の品物を追加したときの解が求められます、
タイプ
ナップザックに入れる個々の品物の個数により、次の3タイプがあります。
タイプ=1 品物は1個だけ
タイプ2 個数は任意
タイプ3 個々の品物に上限がある
注意
データは全て正整数で与えてください。
数値は、なるべく小さい値になるよう単位を調整してください。
全容量は20以下、体積は10以下を想定しています。
タイプ3以外は個数上限は不要です。
入力
var タイプ = 3; // 3=上限指定
var 全容量 = 8;
var 体積 = [2, 4, 1, 3];
var 利益 = [3, 7, 1, 8];
var 個数上限 = [2, 2, 3, 1];
var 表示場所 = "mpKnapsackTest1表示場所";
// タイプ1・2のとき
最適解 = mpKnapsack(タイプ, 全容量, 体積, 利益);
// タイプ3のとき
最適解 = mpKnapsack(タイプ, 全容量, 体積, 利益, 個数上限);
出力 最適解 = mpKnapsack(表示場所, 全容量, 体積, 利益, 個数上限) の戻り値
q↓i→ [q][0] [q][1] [q][2] [q][3]
[0] 0 0 0 0
[1] 0 0 1 0
[2] 1 0 0 0
[3] 0 0 0 1
[4] 0 0 1 1
[5] 1 0 0 1
[6] 0 0 3 1
[7] 0 1 0 1
[8] 0 1 0 1