情報の価値は、その情報を入手したときに、入手しなかったときと比べて、どれだけ利益を得るかで決まります。それには、伝えられた情報の量と情報の内容の重要性の二面があります。このうち、ここでは量の面だけを取り扱います。
1個の硬貨が表か裏かをあてるゲームをするとき、内通者が表だと教えてくれる場合と、サイコロの目が5であることを教えてくれる場合では、後者のほうが情報量が大きいことは常識的にうなずけます。後者の情報量は前者の情報量の何倍になるのかというようなことを数学的に考えようとするのが情報理論です。
ここでは、情報理論の基本的な概念である情報量とエントロピーについて説明します。なお、厳密にはこの情報量のことを選択情報量(自己エントロピー)といい、後述のエントロピーのことを平均情報量(平均エントロピー)といいます。
情報量
- 情報量の定義
- 情報理論では、「ある事象が発生する確率がpであるとき、その事象が必ず発生するという情報を得たときの情報量を log2(1/p) とする」と定義し、情報量の単位を [ビット] としています(JISでは[シャノン]としている)。
硬貨の場合、表である確率はp=1/2ですから、その情報量は log22=1ビットです。サイコロの目が5であることの情報量は log26=2.58 になります。
情報量 I(p) = log2(1/p) = -log2p - log2 について
- log2X は2を低とする対数です。
log22n=n になります。
log2(1/X)= log2X-1 = -log2Xになります。
X 1 2 3 4 6 10 12 13
log2X 0 1 3.58 2 2.58 3.32 3.58 3.70
以下、log2 を log と略記します。 - 例題
-
- 例題1
- 問題
硬貨を2個投げたときに2個が表であることの情報量は何ビットか。
解答
場合の数は、
表-表、表-裏、裏-表、裏-表
の4(=22)通りであり、その確率は同じであるから、表-表である確率は1/4である。
情報量=log4=2 である。 - 例題2
- 問題
硬貨を2個投げたときに、そのうち1個が表なのが見えてしまった。他の1個も表であることの情報量は何ビットか。
解答
硬貨を1個投げたときと同じであるから、情報量=log2=1 となる。
次のように考えることもできる。
新しく得た情報量=全体の情報量 - それまでに得ていた情報量
=2-1=1 - 例題3(有名なクイズ)
- 問題
12個の硬貨のうち、1個が不良品で重さが異なることがわかっている。天秤を用いて不良品を発見するためには、何回天秤にかける必要があるか。
解答
12個のうちから1個であることの情報量は log12=3.58
重いか軽いかを知るための情報量は1
1回の計量で、左=右、左<右、左>右の3通りのうちどれかが判明するので、その情報量は log3=1.58
(3.58+1)/1.58=2.89 → 3回
エントロピー
- エントロピーの定義
- 複数の事象がある場合、それらの情報量の平均値をエントロピー(平均情報量)といいます。
n個の事象、p1, p2, …, pn (p1+p2+ … +pn =1)があるとき、それらの情報量の平均をエントロピーといいます。
エントロピー H = -p1logp1 -p2logp2 - … -pnlogpn - 確率とエントロピー
- 明日雨が降る確率をpとすると、雨が降らない確率は1-pになります。そのときのエントロピーは、
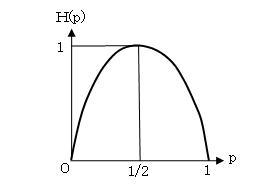
H(p) =-plogp-(1-p)log(1-p)
になります。
pとH(p) の関係をグラフにすると、右図のようになります。
p=1/2のときにHは最大になりますが、これは、信頼の高い天気予報が雨だと予報したときの情報量は、明日雨かどうかが全くわからないときに最大になり、予報を聞く前から(主観的かもしれないが)雨になるだろうと予測できるとき(あるいは雨になる確率が低いと予測できるとき)には、情報量が小さいことを示しています。 - 例題
-
問題
AとBがゲームを行う。Aが勝つ確率は80%、Bが勝つ確率は20%である。このときの情報量とエントロピーを求めよ。
解答
Aが勝つことの情報量:pA=-log0.8=0.32
Bが勝つことの情報量:pB=-log0.2=2.32
エントロピー:H=0.8×0.32+0.2×2.32=0.72
参照
エントロピーの計算や応用に関しては、「1因子情報路による銘柄選択」を参照してください。