| (A,B) | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | ( 3, 1) | (-1,-3) |
| A2 | (-2,-2) | ( 1, 2) | |
右のペイオフ・マトリクスの左側はAの利失で右側はBの利失です。例えばAがA1の戦略を選択してBがB1の戦略を選択したとき,Aは3の利益になり,Bは1の利益になります。このように,Aの利失とBの利失との和が0にならないモデルを非零和ゲームといいます。
多様な戦略
上のペイオフ・マトリクスを用いて,説得,脅迫,協力などの概念を説明します。
他人のペイオフ・マトリクスを知らないとき
AとBが単独に意思決定するとすれば,そのペイオフ・マトリクスは次のようになります。
Aのペイオフ・マトリクス Bのペイオフ・マトリクス (行と列を入れ替えた) B1(q) B2(1-q) A1(p) A2(1-p) A1(p) 3 -1 B1(q) 1 -2 A2(1-p) -2 1 B2(1-q) -3 2
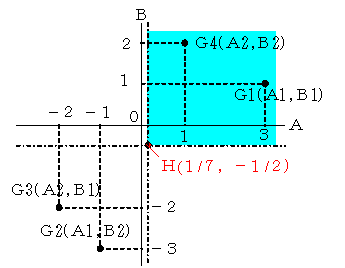
Aのペイオフ・マトリクスを考えましょう。AがA1を選択する確率をp,BがB1を選択する確率をqとすると,ゲームの値VAは,
VA=3pq-1p(1-q)-2(1-p)q+1(1-q)(1-q)
=7(p-3/7)(q-2/7)+1/7
ですから,Aはp=3/7の混合戦略を選択することにより,少なくとも1/7の利益が確保できます。
同様にBのペイオフ・マトリクスについては,
VB=1pq-2(1-p)q-3p(1-q)+2(1-q)(1-q)
=8(p-1/2)(q-5/8)-1/2
より,Bはq=5/8の混合戦略により-1/2の利益を確保します。
すなわち,両者の間にどのような交渉があるにせよ,Aは1/7,Bは-1/2以上の利益(すなわち,右図の青の範囲)がなければ交渉に応じないことになります。それにしてもH点は,G1やG2に比べると利益が少ないですね。ここに駆け引きが生じます。
AがBのペイオフ・マトリクスを知っているとき
AはBのペイオフ・マトリクスを知っているが,BはAのそれを知らないときに,Aはどのような戦略を選択するでしょうか?
- Bを束縛しない
- AはBがq=5/8の混合戦略を選択ことを知っています。そのときの期待値は,
A1: 3×(5/8)-1×(3/8)=12/8=1.5
A2:-2×(5/8)+1×(3/8)=-7/8
になりますので,A1を選択することにより,1/7よりも高い利益,しかも(A1,B1)以外では最高の利益を得ることができます。 - 説得
- AはBのゲームの値-1/2を知っています。-1/2よりも高い利益を保証すれば,Bはそれに応じるでしょう。(A1,B1)をBに提示することにより,Aは3の利益を得ることができます。よしんば(A2,B2)になったとしても1/7よりも高い利益が得られます。
- 脅迫
- Bを説得するのではなく,一方的にA1を選択することをBに伝えることにより,Bは-3を回避するためにB1を選択させます。これにより間違いなく最大利益4を確保することができます。
両者が互いのペイオフ・マトリクスを知っているとき
- 脅迫
- AがA1を選択して脅迫することもできますが,逆にBがB2を選択することをAに伝えて脅迫することもできます。その点では互角ですが,Aは「自分が損失になってもかまわないのでA1を選択する。そうしたらBは重大な損失になる」と逆脅迫する手段が残っています。
- 協力
- 両者の利益合計は(A1,B1)のときが最大値4になります。交渉によりAからBにいくらかの利益を渡すことにも考えられます。その渡す額をいくらにすればよいかに関しても多様な考え方がありますが,ここでは省略します。
有名なゲーム理論モデル
ナッシュ均衡
最適反応とは、「相手の戦略を所与として、自分から戦略を変えても得をしない状態」のことです。そして、Aの取った戦略A1がBの取った戦略B1に対して最適反応であり、B1もA1に対して最適反応であるとき、戦略の組(A1,B1)をナッシュ均衡といいます。ナッシュ均衡が得られれば、A・Bが互いにとっで最適反応なので、戦略を変更する必要がありません。
| (A,B) | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | ( 3, 1) | (-1,-3) |
| A2 | (-2,-2) | ( 1, 2) | |
A・Bの双方が右のペイオフ・マトリクスを知っているとします。
純粋戦略(確率的選択をしない)ならば、
Aの戦略
BがB1を採れば、A1を選択 利益3
BがB2を採れば、A2を選択 利益1 最悪でも1の利益はある
Bの戦略
AがA1を採れば、B1を選択 利益1 最悪でも1の利益はある
AがA2を採れば、B2を選択 利益2
になります。
すなわち(A1,B1)か(A2,B2)のいづれかになります。これをナッシュ均衡といいます。
ナッシュ均衡とは、互いに他者の利益も考慮したときの状態だといえます。
混合戦略ならば、
AがA1を選択する確率をpとしたときのBの純粋戦略での利益は、
B1:1p-2(1-p)3p-2
B2:-3p+2(1-p)=-5p+2
B1=B2とすれば p=1/2、そのときのBの利益は-1/2
すなわち、Aは確率1/2でA1を採ることにより、Bの利益-1/2を保証できます。
BがB1を選択する確率をqとしたときのAの純粋戦略での利益は、
A1:3q-1(1-q)=4q-1
A2:-2q+1(1-q)=-3q+1
A1=A2とすれば q=2/7、そのときのAの利益は1/7
すなわち、Bは確率2/7でB1を採ることにより、Aの利益1/7を保証できます。
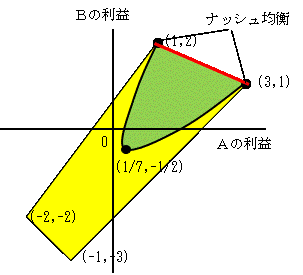
この場合は、(1/7、-1/2)がナッシュ均衡となります。
(この値は「他人のペイオフ・マトリクスを知らないとき」の最適解と同じです。互いに自社戦略を示すことにより、双方が利益を上げることができる例になりました。)
右図での黄色の四角の頂点は純粋戦略で選択できる戦略の組で、四角の中が混合戦略で選択できる領域です。緑の部分は、A・B双方が許容できる領域です。ナッシュ均衡は純粋戦略での(A1,B1)か(A2,B2)になります。どちらになるかは両社の力関係によりますが、両社合計の利益は (3,1) が最大なので、(A1,B1)を選び、AからBへ何らかの供与をすることで決着するのが平和的な解決でしょう。
協調ゲーム
単純なケースでは、両者が互いのペイオフ・マトリクスを示して、ナッシュ均衡を探す方法です。
囚人のジレンマ
| (A,B) | Bの戦略 | B1 | B2 |
|---|---|---|---|
| Aの戦略 | A1 | (0, 0) | (-3, 1) |
| A2 | (1,-3) | (-1,-1) | |
非零和ゲームで有名なモデルに囚人のジレンマがあります。右図のようなペイオフ・マトリクスになります。
二人の囚人AとBが共犯の罪で取り調べを受けています。A1とB1はそれぞれが自白すること,A2とB2は自白しないこととします。(A1,B1)は両者が自白しないときで,そのときは軽微な罪に問われるだけだとして,これを基準として利益0とします。(A2,B2)は両者が自白したときで,罪に服することになります。(A1,B2)と(A2,B1)は一方が自白して他方が自白しないときで,自白者は協力したことにより刑を免れ他者は重刑になるとします。なお,両者ともこのペイオフ・マトリクスは知っているものとします。
- 単独行動をとるとき
- Aのペイオフ・マトリクスだけを取り出すと次のようになります。
A1: 0 -3
A2: 1 -1
A2はA1に優越していますから,AはA2を選択(自白する)します。
ところが同様にBもB2を選択しますので,結果として(-1,-1)になってしまいます。これが好ましい結果とはいえません。 - 協力
- AとBが相談する機会があれば,(A1,B1)になるように約束するでしょう。
- 裏切り
- しかし,その約束は守れらるとはかぎりません。Aは約束に従ってA1を選択(自白しない)したのに,Bは裏切ってB2を選択(自白する)するかもしれないのです。そうなったら,Aは重罪(-3)になってしまいます。
さらに取調官がこのゲームに参画すると,Aに「Bは自白したが,Aは自白しないのか」という虚偽の情報を伝えることにより,(A2,B2)に誘導することも考えられます。
冷戦当時のアメリカとソ連の核戦略を考えましょう。両国とも核を廃絶したいと思っているのですが,自国が廃絶したのに相手が廃絶しなかったら非常な危険があります。しかも,両国が相手を信用していないのですから,いつになっても核を保有し続けることになります。
このように,囚人のジレンマは,互いに最良な事態にする方法を理解しておりその実現を望んでいるのに,相手が信用できないがために,悪い状況から抜け出せないでいる悲劇を説明したり,互いの信用を得ることが重要であることの説明をするのによく用いられています。
トピックス:「買いだめパニック」のゲーム理論的解釈
ゲームの理論は,単なる計算手法は実際の意思決定には役立つことは少ないでしょう。しかし,このような発想方法は,問題を解決するのに非常に役立ちます。
ときどき「トイレットペーパーが買えなくなる」という噂に踊らされて大勢が買いだめに走り、その結果「買えなくなる」現象が実際に発生して、社会問題になることがあります。多くの原因があるでしょうが、ここでは消費者の心理による行動を、協調ゲームや囚人のジレンマから考察します。
自分が思う他人の行動
買いだめをしない 買いだめをする
自分の行動 買いだめをしない A B
買いだめをする C D
- 実は「メーカーには十分な在庫がある」ことは、ほとんどの人が理解しているでしょう。協調ゲームで考えるならば、他人もそのような噂を信じないだろうから、A・Cになる。それなら自分も買いだめをする必要はないので、Aになり、実際にパニックは発生しません。
- ところが、他人はこのような噂を信じるものだと考えるとB・Dになります。トイレットペーパーは日常的にないと困るものだし、それほど高価なものではありません。当面は不要だとしても、買い物ついでに買っておこうかという行動になります。それが他人からはB・Dに見えます。
(このような「ついで買い」を防ぐ(Cを防ぐ)には、一時的に価格を極端に上げればよいという意見があります。社会的にはどうかと思いますが、ゲームの理論からは正論だともいえましょう。) - スーパーでは、資金管理の面から余計な在庫は持たないし、棚の制限もあるので体積の大きな商品を店頭に並べるには制約があります。数人の人が買いだめをするだけで、一時的であっても品切れ状態になります。
- 空の棚を見た人は、他人は買いだめをしていると信じ、大変だとして複数のスーパーを走り回り、できるだけ多くの買いだめをします。これがマスコミで流れると、さらにそう考えがちです。他人は買いだめをしないと理解していても、現実の空き棚を見ると、不安に駆られてCの行動をとります。すなわち、囚人のジレンマの裏切りの状態になります。
- また、スーパーからメーカーへ注文が殺到します。メーカーには在庫があっても流通が追いつきません。緊急配送のため、むしろ効率は低下します。そのため店頭にはなかなか届かず、届いても直ちに買いだめされてしまいます。
- スーパーが「1人1ケース」などの制限をしても、必死になったお客は多数の店舗を走り回るので、ますます事態は深刻になります。
このようにパニックは、疑心暗鬼と過剰な反応に起因します。それを防ぐためにもゲームの理論の考え方を普及する必要があるのでは?