基本事項
- 数学的定義
サイズnの正方行列AとベクトルXがあるとき
、 X’=AX のときX’をXのAによる線形変換の結果の写像といいます。
AX=λX (λはスカラー)が成立するとき、
λをAの固有値といいます。λはn次方程式の根になります(重根、複素根になることもあります)
XをAの固有ベクトルといいます。一つの固有値に一つ以上の固有ベクトルが対応します。
計算は、次の特性方程式で行います。
AX=λX → det(A-λI)=0 からλを計算(det は行列式、Iは単位行列)
(A-λ*I)X=0 から Xを求める。 - 幾何学的意味
固有ベクトル:線形変換しても変わらない向き(ベクトル方向)
固有値:固有ベクトルの長さ - 応用分野
正方行列 P とその逆行列 P-1 があるとき
B=P-1AP を2次形式、BをAの相似行列といいます。
これは、行列で重要な関係式です。
主成分分析など多変量解析やAIの分野で重要な計算に用いられます。
数値例
A=┌3 1┐ とします。
└2 2┘
固有方程式から固有値を求める。
det(A-λI) =│3-λ 1 │= (3-λ)(2-λ)-1・2=0
│ 2 2-λ│ ∴ λ=1、4
固有値λ=1の固有ベクトルを求める。
(A-I)X=┌3-1 1 ┐X=┌2 1┐┌x1┐=┌0┐
└ 2 2-1┘ └2 1┘└x2┘ └0┘
2x1+1x2=0
∴ ┌x1┐=k┌ 1┐ (kは任意の数)
└x2┘ └-2┘
固有値λ=4の固有ベクトルを求める。
(A-4I)X=┌3-4 1 ┐X=┌-1 1┐┌x1┐=┌0┐
└ 2 2-4┘ └ 2 -2┘└x2┘ └0┘
-1x1+1x2=0
2x1-2x2=0
∴ ┌x1┐=k┌1┐ (kは任意の数)
└x2┘ └1┘
イメージ
固有値,固有ベクトルの意味を図により説明します。
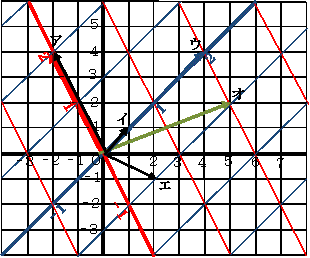
次のようにAとその固有値,固有ベクトルが決まりました。
固有値 固有ベクトル 固有値 固有ベクトル
A=┌3 1┐ λ1=1 k┌ 1┐ λ2=4 k┌1┐
└2 2┘ └-2┘ └1┘
(kは任意のスカラー)
固有ベクトル上の点は、変換後、ベクトルの向きは同じで固有値倍の長さになる
図において、元の座標系を黒のグリッドで示しています。
固有ベクトルk┌ 1┐は、黒グリッドの(1,-2)を通る直線ですから、赤の太線になります。
└-2┘
このベクトルの任意の点(ア)(-2,4)の写像は、┌3 1┐┌-2┐=┌-2┐になり、
└2 2┘└ 4┘ └ 4┘
ベクトルの向きは不変で、長さは1倍(=λ1)になりました。
固有ベクトルk┌1┐は、黒グリッドの(1,1)を通る直線ですから、青の太線になります。
└1┘
このベクトルの任意の点イ(1,1)の写像は、┌3 1┐┌1┐=┌4┐(ウ)になり、
└2 2┘└1┘ └4┘
ベクトルの向きは不変で、長さは4倍(=λ1)になりました。
以上から、固有ベクトル上の点は、変換後、ベクトルの向きは同じで固有値倍の長さになるのです。
固有ベクトル上以外の点ではベクトルの向きが変わる
固有ベクトル上以外の点(エ)┌ 2┐を考えます。
└-1┘
写像(オ)は、┌3 1┐┌ 2┐=┌5┐になります。
└2 2┘└-1┘ └2┘
このように変換を行うと、一般的に黒ベクトルから緑ベクトルへとベクトルの向きが変わります。
赤・青グリッドの目盛り
赤青軸系を斜交座標系といいます。赤軸は黒座標系の縦軸、青軸は黒座標系の横軸に対応します。
点エの黒座標系での位置が(2,-1)だったので、オの斜交座標系での位置も(2,-1)になります。
オから赤ベクトルに平行にたどった青ベクトルの目盛りは2になり、青ベクトルに平行にたどった赤ベクトル目盛りは-1になります。それを基準に等間隔で目盛りをふればよいのです。